【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,同期機のリアクタンスに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
同期機に電機子電流が流れると,その起磁力によって界磁と同期して回転する基本波磁界が空隙(くうげき)中に生じ,これが界磁電流による磁界に影響を及ぼして電機子巻線での誘導起電力を無負荷状態から変化させる。これを電機子反作用といい,電機子反作用磁束に関するリアクタンスを電機子反作用リアクタンスという。任意の力率の電機子反作用磁束は直軸磁束及び横軸磁束に分けることができ,それぞれ対応するリアクタンスを直軸電機子反作用リアクタンス(\( \ X_{\mathrm {ad}} \ \))及び横軸電機子反作用リアクタンス(\( \ X_{\mathrm {aq}} \ \))という。
電機子電流による大部分の磁束は,電機子反作用磁束として電機子巻線及び界磁巻線と鎖交するが,一部の磁束は,電機子巻線だけと鎖交する。これが\( \ \fbox { (1) } \ \)磁束であり,\( \ \fbox { (1) } \ \)リアクタンス(\( \ X_{\mathrm {a}} \ \))に対応する。
界磁電流による大部分の磁束は,電機子巻線及び界磁巻線と鎖交するが,一部の磁束は界磁巻線だけと鎖交する。これが\( \ \fbox { (2) } \ \)磁束であり,\( \ \fbox { (2) } \ \)リアクタンス(\( \ X_{\mathrm {F}} \ \))に対応する。
円筒機のスロット内に収められた制動導体及び導電性くさび並びに突極機の磁極頭部の制動棒に漏れ磁束が存在する。これらの漏れ磁束に対応するのが直軸制動巻線漏れリアクタンス(\( \ X_{\mathrm {Dd}} \ \))及び横軸制動巻線漏れリアクタンス(\( \ X_{\mathrm {Dq}} \ \))である。
各巻線リアクタンスの回路に電機子巻線抵抗,界磁巻線抵抗,直軸及び横軸制動巻線抵抗を加えると,電機子端子側からの直軸及び横軸それぞれの等価回路ができる。この等価回路から,同期機の各リアクタンスを次のように求めることができる。
直軸同期リアクタンス:\( \ X_{\mathrm {d}}=X_{\mathrm {a}}+X_{\mathrm {ad}} \ \)
横軸同期リアクタンス:\( \ X_{\mathrm {q}}=X_{\mathrm {a}}+X_{\mathrm {aq}} \ \)
直軸過渡リアクタンス:\( \ X_{\mathrm {d}}^{\prime }= \ \fbox { (3) } \ \)
直軸初期過渡リアクタンス:\( \ X_{\mathrm {d}}^{\prime \prime }= \ \fbox { (4) } \ \)
横軸初期過渡リアクタンス:\( \ X_{\mathrm {q}}^{\prime \prime }= \ \fbox { (5) } \ \)
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 界磁漏れ &(ロ)& \frac {\left( X_{\mathrm {a}}+X_{\mathrm {ad}}\right) \cdot X_{\mathrm {F}}\cdot X_{\mathrm {Dd}}}{\left( X_{\mathrm {a}}+X_{\mathrm {ad}}\right) \left( X_{\mathrm {F}}+X_{\mathrm {Dd}}\right) +X_{\mathrm {F}}\cdot X_{\mathrm {Dd}}} \\[ 5pt ]
&(ハ)& 電機子鎖交 &(ニ)& X_{\mathrm {a}}+X_{\mathrm {Dq}} \\[ 5pt ]
&(ホ)& X_{\mathrm {a}}+\frac {X_{\mathrm {ad}}\cdot X_{\mathrm {F}}}{X_{\mathrm {ad}}+ X_{\mathrm {F}}} &(ヘ)& 界磁鎖交 \\[ 5pt ]
&(ト)& \frac {\left( X_{\mathrm {a}}+X_{\mathrm {aq}}\right) \cdot X_{\mathrm {Dq}}}{ X_{\mathrm {a}}+X_{\mathrm {aq}}+X_{\mathrm {Dq}}} &(チ)& \frac {\left( X_{\mathrm {a}}+X_{\mathrm {ad}}\right) \cdot X_{\mathrm {F}}}{ X_{\mathrm {a}}+X_{\mathrm {ad}}+X_{\mathrm {F}}} \\[ 5pt ]
&(リ)& X_{\mathrm {a}}+\frac {X_{\mathrm {ad}}\cdot X_{\mathrm {F}}\cdot X_{\mathrm {Dd}}}{X_{\mathrm {ad}}\cdot X_{\mathrm {F}}+X_{\mathrm {ad}}\cdot X_{\mathrm {Dd}}+X_{\mathrm {F}}\cdot X_{\mathrm {Dd}} } &(ヌ)& X_{\mathrm {a}}+\frac {X_{\mathrm {aq}}\cdot X_{\mathrm {Dq}}}{X_{\mathrm {aq}}+ X_{\mathrm {Dq}}} \\[ 5pt ]
&(ル)& 固定子鎖交 &(ヲ)& 電機子漏れ \\[ 5pt ]
&(ワ)& X_{\mathrm {a}}+X_{\mathrm {F}} &(カ)& 回転子鎖交 \\[ 5pt ]
&(ヨ)& X_{\mathrm {a}}+X_{\mathrm {Dd}} && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ 1 \ \)種の同期機は本問のようにやや高度な問題が出題されやすく,\( \ 2 \ \)種や\( \ 3 \ \)種で使用した参考書には掲載されていないと思います。
やや専門的な内容となりますが,知識として概要を習得していれば解ける問題となりますので,確実に理解して得点できるようになりましょう。
1.同期機の\( \ \mathrm {d} \ \)軸成分等価回路と\( \ \mathrm {q} \ \)軸成分等価回路
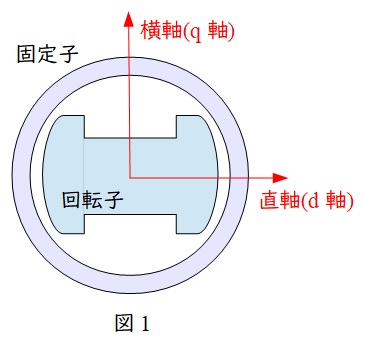
同期機の回転子の磁極と同じ向きの軸を直軸(\( \ \mathrm {d} \ \)軸),磁極と直角の向きの軸を横軸(\( \ \mathrm {q} \ \)軸)としたときの等価回路は図2及び図3のようになります。
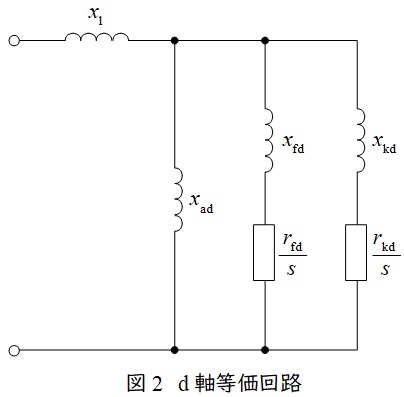
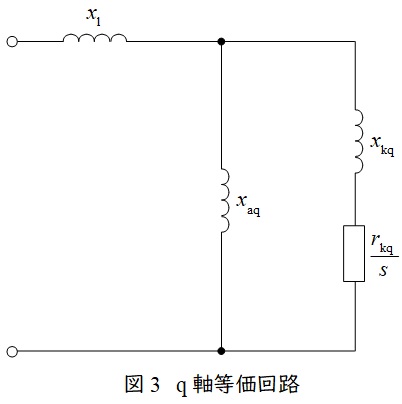
\( \ x_{\mathrm {l}} \ \):電機子巻線漏れリアクタンス, \( \ x_{\mathrm {ad}},x_{\mathrm {aq}} \ \):電機子反作用リアクタンス
\( \ r_{\mathrm {fd}} \ \):界磁巻線抵抗, \( \ x_{\mathrm {fd}} \ \):界磁巻線リアクタンス
\( \ r_{\mathrm {kd}},r_{\mathrm {kq}} \ \):制動巻線抵抗, \( \ x_{\mathrm {kd}},x_{\mathrm {kq}} \ \):制動巻線リアクタンス
\( \ s \ \):ラプラス演算子
2.初期過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime \prime} \ \)と過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime} \ \),同期リアクタンス\( \ X_{\mathrm {d}} \ \)
図2において,過渡現象が始まって数サイクルの間は\( \ s \ \)が非常に大きく,界磁巻線抵抗及び制動巻線抵抗とも無視できるほど小さくなるので,界磁巻線リアクタンスと制動巻線リアクタンスを考慮します。これを初期過渡リアクタンスと呼びます。
次に数サイクル~\( \ 1.0 \ \)秒程度の間は\( \ s \ \)は少し小さくなり,\( \ r_{\mathrm {fd}} \ < \ r_{\mathrm {kd}} \ \)ため,界磁巻線抵抗は無視できますが制動巻線抵抗は無視できなくなるので,界磁巻線リアクタンスと電機子のリアクタンスを考慮すれば良くなります。これを過渡リアクタンスと呼びます。
\( \ 1.0 \ \)秒以降は\( \ s \ \)の値が小さくなるので,界磁巻線抵抗及び制動巻線抵抗が無視できなくなるので,電機子のリアクタンスのみ考慮すればよくなります。これを同期リアクタンスと呼びます。
【解答】
(1)解答:ヲ
題意より解答候補は,(イ)界磁漏れ,(ハ)電機子鎖交,(ヘ)界磁鎖交,(ル)固定子鎖交,(ヲ)電機子漏れ,(カ)回転子鎖交,になると思います。
ワンポイント解説「1.同期機の\( \ \mathrm {d} \ \)軸成分等価回路と\( \ \mathrm {q} \ \)軸成分等価回路」の通り,電機子巻線と鎖交する磁束に対応するリアクタンスは電機子漏れリアクタンスとなります。
(2)解答:イ
題意より解答候補は,(イ)界磁漏れ,(ハ)電機子鎖交,(ヘ)界磁鎖交,(ル)固定子鎖交,(ヲ)電機子漏れ,(カ)回転子鎖交,になると思います。
ワンポイント解説「1.同期機の\( \ \mathrm {d} \ \)軸成分等価回路と\( \ \mathrm {q} \ \)軸成分等価回路」の通り,界磁巻線と鎖交する磁束に対応するリアクタンスは界磁漏れリアクタンスとなります。
(3)解答:ホ
ワンポイント解説「2.初期過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime \prime} \ \)と過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime} \ \),同期リアクタンス\( \ X_{\mathrm {d}} \ \)」の通り,過渡リアクタンスを検討する場合においては界磁漏れリアクタンス\( \ X_{\mathrm {F}} \ \)と直軸電機子反作用リアクタンス\( \ X_{\mathrm {ad}} \ \)を考慮すれば良いため,\( \ \mathrm {d} \ \)軸等価回路の合成リアクタンスを求めると,
\[
\begin{eqnarray}
X_{\mathrm {d}}^{\prime } &=& X_{\mathrm {a}}+\frac {X_{\mathrm {ad}}\cdot X_{\mathrm {F}}}{X_{\mathrm {ad}}+ X_{\mathrm {F}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
ワンポイント解説「2.初期過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime \prime} \ \)と過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime} \ \),同期リアクタンス\( \ X_{\mathrm {d}} \ \)」の通り,初期過渡リアクタンスを求めるためには全てのリアクタンスを考慮する必要があるので,
\[
\begin{eqnarray}
X_{\mathrm {d}}^{\prime \prime } &=& X_{\mathrm {a}}+\frac {1}{\displaystyle \frac {1}{X_{\mathrm {ad}}}+\frac {1}{X_{\mathrm {F}}}+\frac {1}{X_{\mathrm {Dd}}}} \\[ 5pt ]
&=& X_{\mathrm {a}}+\frac {1}{ \displaystyle \frac {X_{\mathrm {ad}}\cdot X_{\mathrm {F}}+X_{\mathrm {ad}}\cdot X_{\mathrm {Dd}}+X_{\mathrm {F}}\cdot X_{\mathrm {Dd}} }{X_{\mathrm {ad}}\cdot X_{\mathrm {F}}\cdot X_{\mathrm {Dd}}}} \\[ 5pt ]
&=& X_{\mathrm {a}}+\frac {X_{\mathrm {ad}}\cdot X_{\mathrm {F}}\cdot X_{\mathrm {Dd}}}{X_{\mathrm {ad}}\cdot X_{\mathrm {F}}+X_{\mathrm {ad}}\cdot X_{\mathrm {Dd}}+X_{\mathrm {F}}\cdot X_{\mathrm {Dd}} } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヌ
(4)と同様に,横軸初期過渡リアクタンスを求めると,
\[
\begin{eqnarray}
X_{\mathrm {q}}^{\prime \prime } &=& X_{\mathrm {a}}+\frac {X_{\mathrm {aq}}\cdot X_{\mathrm {Dq}}}{X_{\mathrm {aq}}+ X_{\mathrm {Dq}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん