【問題】
【難易度】★★☆☆☆(やや易しい)
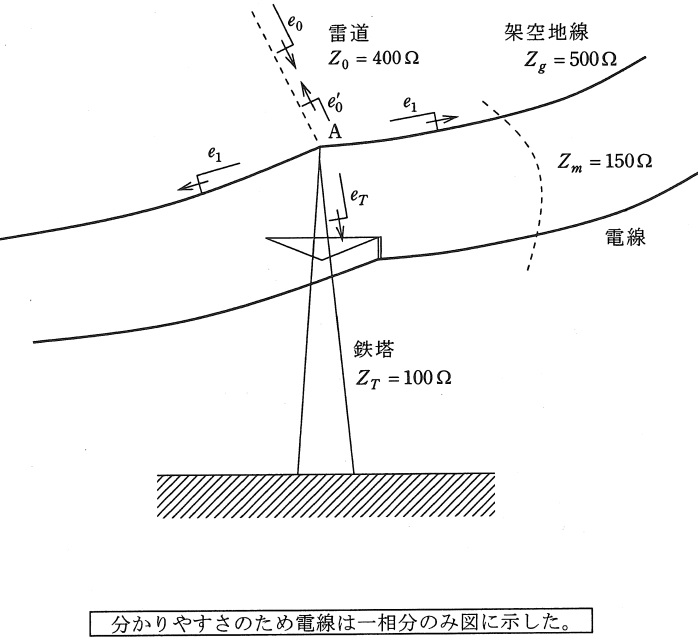
図に示すように,自己サージインピーダンス\( \ Z_{g} \ \)が\( \ 500 \ \mathrm {[\Omega ]} \ \)の架空地線\( \ 1 \ \)条を有する三相\( \ 1 \ \)回線送電線路鉄塔の頂部\( \ \mathrm {A} \ \)点に雷の直撃を受けた。この場合,雷撃後のがいしにかかる電圧の最大値に関して,次の問に答えよ。ただし,雷電圧はその波形が方形波(矩形波)で,波高値\( \ e_{0} \ \)は\( \ 10 \ 000 \ \mathrm {[kV]} \ \)であり,雷道のサージインピーダンス\( \ Z_{0} \ \)は\( \ 400 \ \mathrm {[\Omega ]} \ \),架空地線と電線との相互サージインピーダンス\( \ Z_{m} \ \)は\( \ 150 \ \mathrm {[\Omega ]} \ \),鉄塔のサージインピーダンス\( \ Z_{T} \ \)は\( \ 100 \ \mathrm {[\Omega ]} \ \)とする。なお,電線の商用周波の常規対地電圧は無視し,鉄塔と架空地線及び鉄塔と電線との間の相互サージインピーダンス,並びに鉄塔の塔脚接地抵抗は無視するものとする。また,以下の問において電圧,電流はそれぞれ\( \ e \ \),\( \ i \ \)で表すものとする。
(1) 雷道を通ってくる雷の入射波を\( \ e_{0} \ \),\( \ i_{0} \ \),雷道への反射波を\( \ e^{\prime }_{0} \ \),\( \ i^{\prime }_{0} \ \),架空地線への侵入波を\( \ e_{1} \ \),\( \ i_{1} \ \),鉄塔への侵入波を\( \ e_{T} \ \),\( \ i_{T} \ \)としたときの鉄塔頂部\( \ \mathrm {A} \ \)点における雷撃直後の電圧,電流について成り立つ関係式をすべて示せ。
(2) 雷撃直後の鉄塔頂部\( \ \mathrm {A} \ \)点の電圧を求める計算式を示し,その値を求めよ。
(3) 雷撃後のがいしにかかる電圧の最大値を求める計算式を示し,その値を求めよ。
【ワンポイント解説】
鉄塔に落雷したときの各所の電圧値の変化を求める問題です。
理論科目で出題されることが多い分布定数回路の応用問題という印象です。\( \ 1 \ \)種の二次試験としては,比較的理解しやすい計算問題の部類に入るかと思います。
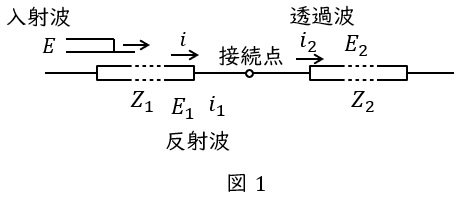
1.分布定数回路における接続点での関係式
図1のような,特性インピーダンスが\( \ Z_{1} \ \)及び\( \ Z_{2} \ \)の非常に長い無損失線路が接続されているときの接続点での関係式を考えます。
図の左側から波高値\( \ E \ \)の電圧波が進入すると,接続点で一部の電圧が反射し,残りの電圧が透過します。このとき,入射波による電流を\( \ i \ \),反射波により生じる電圧及び電流を\( \ E_{1} \ \)及び\( \ i_{1} \ \),透過波により生じる電圧及び電流を\( \ E_{2} \ \)及び\( \ i_{2} \ \)とし,いずれの電流も右向きに流れる電流を正とすると,以下の電圧と電流の関係式が成り立ちます。
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ]
i +i_{1}&=&i_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,各電圧と電流には,
\[
\begin{eqnarray}
E&=&Z_{1}i \\[ 5pt ]
E_{1}&=&-Z_{1}i_{1} \\[ 5pt ]
E_{2}&=&Z_{2}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
※ 右向きを正とするので,電流\( \ i_{1} \ \)が負の値になることに注意しましょう。
【解答】
(1)鉄塔頂部\( \ \mathrm {A} \ \)点における雷撃直後の電圧,電流について成り立つ関係式
ワンポイント解説「1.分布定数回路における接続点での関係式」の通り,電圧及び電流の関係式は,
\[
\begin{eqnarray}
e_{0}+e^{\prime }_{0}&=&e_{1}=e_{T} & \ ・・・・・・・・・・・・・ ①& \\[ 5pt ]
i_{0}+i_{0}^{\prime }&=&2i_{1}+i_{T} & \ ・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となり,各電圧と電流の関係式は,
\[
\begin{eqnarray}
e_{0}&=&Z_{0}i_{0} &・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
e^{\prime }_{0}&=&-Z_{0}i_{0}^{\prime } &・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
e_{1}&=&Z_{g}i_{1} &・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
e_{T}&=&Z_{T}i_{T} &・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)雷撃直後の鉄塔頂部\( \ \mathrm {A} \ \)点の電圧を求める計算式とその値
雷撃直後の鉄塔頂部\( \ \mathrm {A} \ \)点の電圧は\( \ e_{1}\left( =e_{T}\right) \ \)である。
③~⑥を電流値について整理し,②に代入すると,
\[
\begin{eqnarray}
i_{0}+i_{0}^{\prime }&=&2i_{1}+i_{T} \\[ 5pt ]
\frac {e_{0}}{Z_{0}}-\frac {e^{\prime }_{0}}{Z_{0}}&=&\frac {2e_{1}}{Z_{g}}+\frac {e_{T}}{Z_{T}} \\[ 5pt ]
e_{0}-e^{\prime }_{0}&=&Z_{0}\left( \frac {2e_{1}}{Z_{g}}+\frac {e_{T}}{Z_{T}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,①より\( \ e_{1}=e_{T} \ \)であるから,
\[
\begin{eqnarray}
e_{0}-e^{\prime }_{0}&=&Z_{0}\left( \frac {2e_{1}}{Z_{g}}+\frac {e_{1}}{Z_{T}}\right) \\[ 5pt ]
&=&Z_{0}e_{1}\left( \frac {2}{Z_{g}}+\frac {1}{Z_{T}}\right) \\[ 5pt ]
&=&\frac {Z_{0}\left( 2Z_{T}+Z_{g}\right) }{Z_{g}Z_{T}}e_{1} &・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ①+⑦ \ \)より,
\[
\begin{eqnarray}
2e_{0}&=&e_{1}+\frac {Z_{0}\left( 2Z_{T}+Z_{g}\right) }{Z_{g}Z_{T}}e_{1} \\[ 5pt ]
&=&e_{1}\left\{ 1+\frac {Z_{0}\left( 2Z_{T}+Z_{g}\right) }{Z_{g}Z_{T}}\right\} \\[ 5pt ]
&=&e_{1}\frac {Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}}{Z_{g}Z_{T}} \\[ 5pt ]
e_{1}&=&e_{0}\frac {2Z_{g}Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,各値を代入すれば,
\[
\begin{eqnarray}
e_{1}&=&10 \ 000 \times 10^{3}\times \frac {2\times 500\times 100}{500\times 100+2\times 100\times 400+400\times 500} \\[ 5pt ]
&≒&3 \ 030.3 \times 10^{3} \ \mathrm {[V]} → 3 \ 030 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)雷撃後のがいしにかかる電圧の最大値を求める計算式とその値
雷撃後のがいしにかかる電圧の最大値\( \ e_{m} \ \)は,\( \ e_{T}\left( =e_{1}\right) \ \)と雷撃後の電線の電圧\( \ e_{L} \ \)の差となる。
雷撃後の電線の電圧\( \ e_{L} \ \)は,相互サージインピーダンス\( \ Z_{m} \ \)より,
\[
\begin{eqnarray}
e_{L}&=&Z_{m}i_{1} \\[ 5pt ]
&=&Z_{m}\cdot \frac {e_{1}}{Z_{g}} \\[ 5pt ]
&=&Z_{m}\cdot \frac {1}{Z_{g}}e_{0}\frac {2Z_{g}Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}} \\[ 5pt ]
&=&e_{0}\frac {2Z_{m}Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,雷撃後のがいしにかかる電圧の最大値\( \ e_{m} \ \)は,
\[
\begin{eqnarray}
e_{m}&=&e_{1}-e_{L} \\[ 5pt ]
&=&e_{0}\frac {2Z_{g}Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}}-e_{0}\frac {2Z_{m}Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}} \\[ 5pt ]
&=&e_{0}\frac {2\left( Z_{g}-Z_{m}\right)Z_{T}}{Z_{g}Z_{T}+2Z_{T}Z_{0}+Z_{0}Z_{g}} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,各値を代入すれば,
\[
\begin{eqnarray}
e_{m}&=&10 \ 000 \times 10^{3}\times \frac {2\times \left( 500-150\right) \times 100}{500\times 100+2\times 100\times 400+400\times 500} \\[ 5pt ]
&≒&2 \ 121.2 \times 10^{3} \ \mathrm {[V]} → 2 \ 120 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん