【問題】
【難易度】★★★★☆(やや難しい)
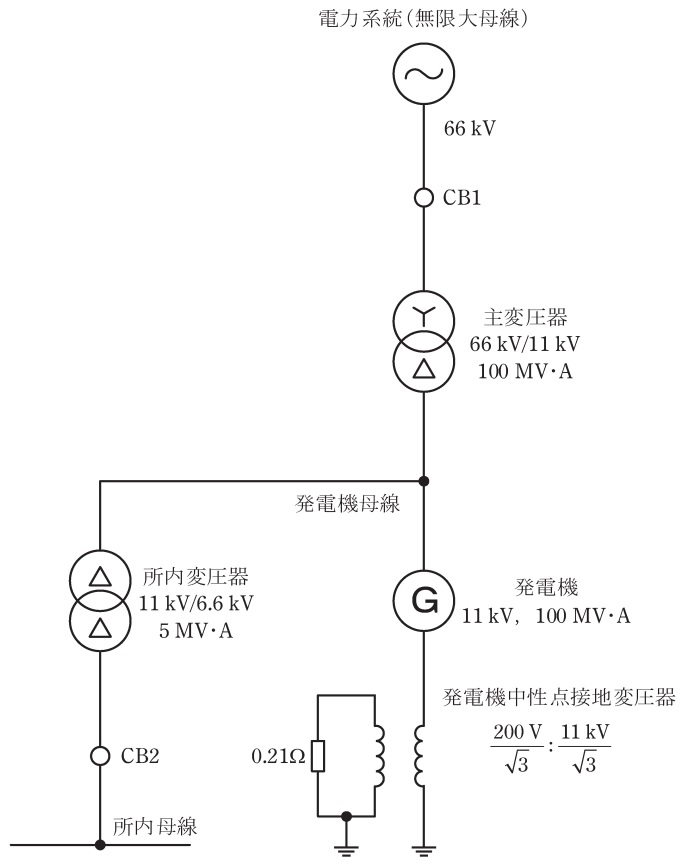
電圧\( \ 11 \ \mathrm {kV} \ \),容量\( \ 100 \ \mathrm {MV\cdot A} \ \)の三相発電機が主変圧器を介して\( \ 66 \ \mathrm {kV} \ \)送電線に接続する系統がある。主変圧器の容量は,\( \ 100 \ \mathrm {MV\cdot A} \ \)であり,インピーダンスは自己容量ベースで\( \ 9 \ \mathrm {%} \ \)である。\( \ 66 \ \mathrm {kV} \ \)送電線系統は,無限大母線と考えてよい。発電機巻線は星形結線であり,その中性点は図のように接地変圧器及び接地抵抗によって接地されている。\( \ 11 \ \mathrm {kV} \ \)発電機母線には,補機に電力を供給するための所内変圧器が接続されている。所内変圧器容量は\( \ 5 \ \mathrm {MV\cdot A} \ \)であり,所内母線電圧は\( \ 6.6 \ \mathrm {kV} \ \)である。発電機の短絡比が\( \ 0.6 \ \)であるとき,次の問に答えよ。
ただし,発電機は発電機電圧\( \ 11 \ \mathrm {kV} \ \)で運転中であり,送電線運転電圧は\( \ 66 \ \mathrm {kV} \ \)であるとする。発電機,変圧器の巻線抵抗は,無視してよい。
(1) 発電機母線で三相短絡が生じたときの短絡電流の大きさはいくらか。主変圧器の\( \ 11 \ \mathrm {kV} \ \)端子から流れ込む電流と,発電機から供給される電流とに分けて解答せよ。なお,所内母線側からの電流供給はないものとする。
(2) 所内母線受電遮断器\( \ \mathrm {CB2} \ \)の遮断電流が\( \ 12.5 \ \mathrm {kA} \ \)であるとする。所内母線三相短絡時に\( \ \mathrm {CB2} \ \)を流れる電流を\( \ 12.5 \ \mathrm {kA} \ \)以下とするためには,所内変圧器のインピーダンスの大きさを何パーセント(自己容量ベース)以上としなければならないか。ただし,発電機の内部相差角は,無視してよい。
(3) 発電機母線が完全一線地絡したときの地絡電流の大きさは,何アンペアとなるか。ただし,発電機の正相,逆相,零相インピーダンスは,無視してよい。
【ワンポイント解説】
三相短絡電流及地絡電流の導出を問う問題となります。
令和\( \ 2 \ \)年度の問題の中では最も\( \ 1 \ \)種らしい問題で,まともに解くと少し時間を要する問題なので,試験で選択されることはオススメしませんが,練習問題としては様々な公式や解法を取り扱う良問なので,非常に良い問題と言えると思います。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法における容量換算
「1.オーム法から単位法への変換」の通り,単位法のインピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の単位法におけるインピーダンスは,
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.単位法の短絡電流計算
単位法における短絡インピーダンスを\( \ Z \ \mathrm {[p.u.]} \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{Z \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※単位法の定義式等を用いて上式を導出することはできますが,試験時には暗記しておいた方が良いと思います。
4.短絡比\( \ K_{\mathrm {s}} \ \)と単位法で表した同期インピーダンス\( \ Z_{\mathrm {s}} \ \)との関係
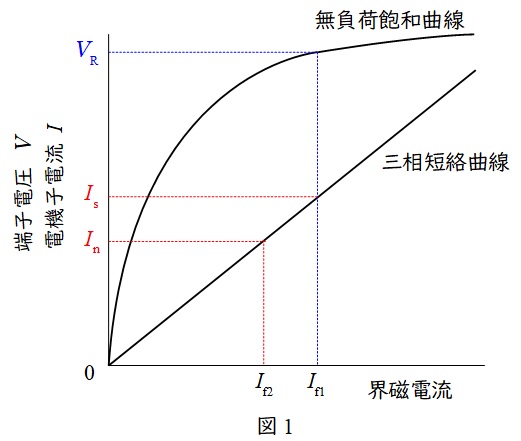
同期発電機の特性曲線は図1のように描けられ,短絡比\( \ K_{\mathrm {s}} \ \)は次のように定義されます。
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ]
&=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
短絡比\( \ K_{\mathrm {s}} \ \)と単位法で表した同期インピーダンス\( \ Z_{\mathrm {s}} \ \)との関係は,
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}}}{I_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}I_{\mathrm {n}}}\\[ 5pt ]
&=& \frac {1}{Z_{\mathrm {s}}\mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
となります。(公式として暗記しておきましょう。)
【解答】
(1)発電機母線で三相短絡が生じたときの短絡電流を主変圧器の\( \ 11 \ \mathrm {kV} \ \)端子から流れ込む電流と,発電機から供給される電流とに分けて求める
基準容量\( \ P_{\mathrm {n}}=100 \ \mathrm {[MV\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}}=11 \ \mathrm {[kV]} \ \)とすると,基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {100\times 10^{6}}{\sqrt {3}\times 11 \times 10^{3}} \\[ 5pt ]
&≒&5248.6 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
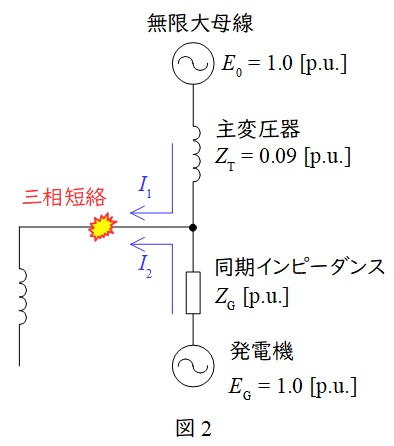
となる。題意より,発電機母線で三相短絡が生じたときの等価回路は図2のように描けるので,主変圧器の\( \ 11 \ \mathrm {kV} \ \)端子から流れ込む電流\( \ I_{\mathrm {1}} \ \mathrm {[A]} \ \)は,ワンポイント解説「3.単位法の短絡電流計算」の通り,
\[
\begin{eqnarray}
I_{\mathrm {1}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {T}}} \\[ 5pt ]
&=&\frac {5248.6}{0.09} \\[ 5pt ]
&≒&58318 \ \mathrm {[A]} → 58.3 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。発電機の短絡比\( \ K_{\mathrm {s}}=0.6 \ \)より,図2における発電機の同期インピーダンス\( \ Z_{\mathrm {G}} \ \)は,ワンポイント解説「4.短絡比\( \ K_{\mathrm {s}} \ \)と単位法で表した同期インピーダンス\( \ Z_{\mathrm {s}} \ \)との関係」の通り,
\[
\begin{eqnarray}
Z_{\mathrm {G}}&=&\frac {1}{K_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1}{0.6} \\[ 5pt ]
&≒&1.6667 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,発電機から供給される電流\( \ I_{\mathrm {2}} \ \mathrm {[A]} \ \)は,ワンポイント解説「3.単位法の短絡電流計算」の通り,
\[
\begin{eqnarray}
I_{\mathrm {2}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {G}}} \\[ 5pt ]
&=&\frac {5248.6}{1.6667} \\[ 5pt ]
&≒&3149.1 \ \mathrm {[A]} → 3.15 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
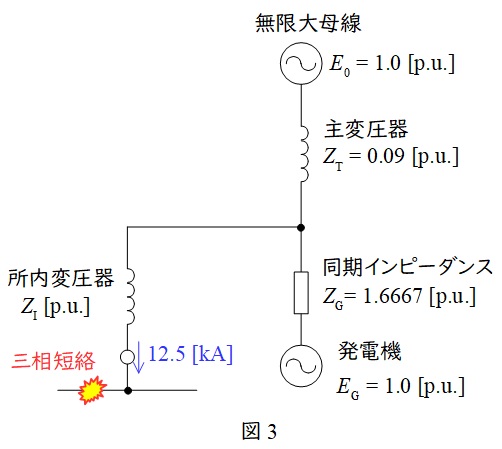
(2)所内母線三相短絡時に\( \ \mathrm {CB2} \ \)を流れる電流を\( \ 12.5 \ \mathrm {kA} \ \)以下とするためには,所内変圧器のインピーダンスの大きさを何パーセント(自己容量ベース)以上としなければならないか
題意に沿って等価回路を描くと図3のようになる。所内変圧器のインピーダンスを\( \ Z_{\mathrm {I}} \ \)とし,これを\( \ 100 \ \mathrm {MV\cdot A} \ \)換算すると,ワンポイント解説「2.単位法における容量換算」の通り,
\[
\begin{eqnarray}
\frac {100}{5}Z_{\mathrm {I}}&=&20Z_{\mathrm {I}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図3の合成インピーダンス\( \ Z \ \)は,
\[
\begin{eqnarray}
Z&=&\frac {Z_{\mathrm {T}}Z_{\mathrm {G}}}{Z_{\mathrm {T}}+Z_{\mathrm {G}}}+20Z_{\mathrm {I}} \\[ 5pt ]
&=&\frac {0.09\times 1.6667}{0.09+1.6667}+20Z_{\mathrm {I}} \\[ 5pt ]
&≒&0.085389+20Z_{\mathrm {I}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,所内回路の基準電流\( \ I_{\mathrm {n}}^{\prime } \ \mathrm {[A]} \ \)は,基準容量\( \ P_{\mathrm {n}}=100 \ \mathrm {[MV\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}}^{\prime }=6.6 \ \mathrm {[kV]} \ \)とすると,
\[
\begin{eqnarray}
I_{\mathrm {n}}^{\prime }&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}^{\prime }} \\[ 5pt ]
&=&\frac {100\times 10^{6}}{\sqrt {3}\times 6.6 \times 10^{3}} \\[ 5pt ]
&≒&8747.7 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,短絡電流の大きさ\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は,ワンポイント解説「3.単位法の短絡電流計算」の通り,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}^{\prime }}{Z} \\[ 5pt ]
&=&\frac {8747.7}{0.085389+20Z_{\mathrm {I}}} \\[ 5pt ]
\end{eqnarray}
\]
となるが,題意より\( \ \mathrm {CB2} \ \)を流れる電流を\( \ 12.5 \ \mathrm {kA} \ \)以下とする必要があるので,
\[
\begin{eqnarray}
12.5\times 10^{3}&≧&\frac {8747.7}{0.085389+20Z_{\mathrm {I}}} \\[ 5pt ]
0.085389+20Z_{\mathrm {I}}&≧&\frac {8747.7}{12.5\times 10^{3}} \\[ 5pt ]
20Z_{\mathrm {I}}&≧&\frac {8747.7}{12.5\times 10^{3}}-0.085389 \\[ 5pt ]
Z_{\mathrm {I}}&≧&0.030721 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,所内変圧器のインピーダンスの大きさは\( \ 3.08 \ \mathrm {%} \ \)以上としなければならないことがわかる。
(3)発電機母線が完全一線地絡したときの地絡電流の大きさ
発電機接地抵抗を\( \ 11 \ \mathrm {kV} \ \)母線側に換算した大きさ\( \ R_{\mathrm {E}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {E}}&=&\left( \frac {11\times 10^{3}}{200}\right)^{2}\times 0.21 \\[ 5pt ]
&=&635.25 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であり,発電機の正相,逆相,零相インピーダンスは無視できるので,地絡電流の大きさ\( \ I_{\mathrm {g}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {g}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{R_{\mathrm {E}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {11\times 10^{3}}{\sqrt {3}}}{635.25} \\[ 5pt ]
&≒&10.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん