《機械》〈照明〉[H22:問6]異なる2種類の光源の水平面照度の比較に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

$ \ \mathrm {A} \ $及び$ \ \mathrm {B} \ $の$ \ 2 \ $種類の$ \ \mathrm {LED} \ $ランプが，次の条件で設置されているとき，$ \ \mathrm {A} \ $と$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプによる鉛直角$ \ 60° \ $方向の床面の水平面照度を比較し，$ \ \mathrm {B} \ $が$ \ \mathrm {A} \ $の何倍の照度になるかを調べたい。次の手順に従って，文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な数値を解答群の中から選びなさい。

$ \ \mathrm {A} \ $及び$ \ \mathrm {B} \ $の$ \ 2 \ $種類の$ \ \mathrm {LED} \ $ランプが，$ \ 2 \ \mathrm {[m]} \ $の高さに下向きに設置されている。$ \ \mathrm {A} \ $の$ \ \mathrm {LED} \ $ランプは,その直下の床面の水平面照度が$ \ 500 \ \mathrm {[lx]} \ $であり，配光が$ \ I_{\mathrm {A}}\left( \theta \right) =I_{\mathrm {A}}\left( 0 \right) \cos ^{4}\theta \ $なる軸対称配光である。$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプは，その直下の床面の水平面照度が$ \ \mathrm {A} \ $の$ \ 0.6 \ $倍の$ \ 300 \ \mathrm {[lx]} \ $であり，配光が$ \ I_{\mathrm {B}}\left( \theta \right) =I_{\mathrm {B}}\left( 0 \right) \cos \theta \ $なる軸対称配光である。

ここに，$ \ I_{\mathrm {A}}\left( 0 \right) \ $，$ \ I_{\mathrm {B}}\left( 0 \right) \ $は，それぞれ$ \ \mathrm {A} \ $及び$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプの直下方向の光度，$ \ I_{\mathrm {A}}\left( \theta \right) \ $，$ \ I_{\mathrm {B}}\left( \theta \right) \ $は，それぞれ$ \ \mathrm {A} \ $及び$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプの鉛直角$ \ \theta \ $方向の光度とする。

また，$ \ \sin 60° = 0.866 \ $，$ \ \cos 60° = 0.5 \ $とする。

$ \ \mathrm {A} \ $の$ \ \mathrm {LED} \ $ランプは，その直下の水平面照度が$ \ 500 \ \mathrm {[lx]} \ $なので，これを直下方向の光度$ \ I_{\mathrm {A}}\left( 0 \right) \ $に換算すると$ \ \fbox {　（１）　} \ \mathrm {[cd]} \ $であり，鉛直角$ \ 60° \ $方向の光度$ \ I_{\mathrm {A}}\left( 60 \right) \ $を求めると$ \ \fbox {　（２）　} \ \mathrm {[cd]} \ $になる。これより，鉛直角$ \ 60° \ $方向の床面の水平面照度を求めると$ \ \fbox {　（３）　} \ \mathrm {[lx]} \ $になる。

同様の手順で，$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプの鉛直角$ \ 60° \ $方向の床面の水平面照度を求めると，$ \ \fbox {　（４）　} \ \mathrm {[lx]} \ $となる。

したがって，鉛直角$ \ 60° \ $方向の床面の水平面照度は，$ \ \mathrm {B} \ $が$ \ \mathrm {A} \ $の$ \ \fbox {　（５）　} \ $倍の照度になる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　2 \ 000　　　　　&（ロ）&　1.2　　　　　&（ハ）&　3.9　　　　　&（ニ）&　15.6 \\[ 5pt ] &（ホ）&　62.5　　　　　&（ヘ）&　9.4　　　　　&（ト）&　1 \ 000　　　　　&（チ）&　2.3 \\[ 5pt ] &（リ）&　7.8　　　　　 &（ヌ）&　500　　　　　&（ル）&　4.8　　　　　　&（ヲ）&　31.3 \\[ 5pt ] &（ワ）&　125　　　　　&（カ）&　2.0　　　　　&（ヨ）&　18.8　　　　　&（タ）&　2.4 \\[ 5pt ] &（レ）&　9.6　　　　　&& && && \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

照度及び配向特性の異なる$ \ 2 \ $種類の光源の水平面照度の比較に関する問題です。
平成22年度機械科目の全体の難易度を考えるとこの問題はできれば完答したい問題となります。
こういう問題を計算ミスせずに解けるようになると，合格は一気に近づくことになるかと思います。

1.光度$ \ I \ $
ある方向に向かう光束$ \ F \ \mathrm {[lm]} \ $を立体角$ \ \omega \ \mathrm {[sr]} \ $で割ったものが光度$ \ I \ \mathrm {[cd]} \ $となります。
\[
\begin{eqnarray}
I &=&\frac {\Delta F}{\Delta \omega } \\[ 5pt ] \end{eqnarray}
\]

2.水平面照度$ \ E_{\mathrm {h}} \ $
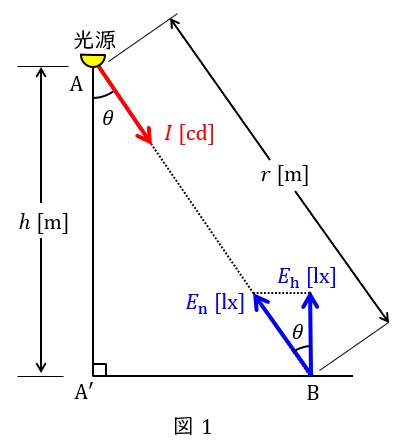
図1のように，点光源から光度$ \ I \ \mathrm {[cd]} \ $で$ \ \mathrm {B} \ $点に向かって光が照射されているとき，法線照度$ \ E_{\mathrm {n}} \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {n}} &=&\frac {I}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められ，水平面照度$ \ E_{\mathrm {h}} \ \mathrm {[lx]} \ $は，$ \ E_{\mathrm {n}} \ \mathrm {[lx]} \ $の余弦$ \ \cos \theta \ $であるから，
\[
\begin{eqnarray}
E_{\mathrm {h}} &=&E_{\mathrm {n}}\cos \theta \\[ 5pt ] &=&\frac {I}{r^{2}}\cdot \frac {h}{r} \\[ 5pt ] &=&\frac {hI}{r^{3}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：イ
$ \ \mathrm {A} \ $の$ \ \mathrm {LED} \ $ランプは，その直下の水平面照度が$ \ E_{\mathrm {A}}\left( 0 \right) =500 \ \mathrm {[lx]} \ $及び高さ$ \ h=2 \ \mathrm {[m]} \ $なので，直下方向の光度$ \ I_{\mathrm {A}}\left( 0 \right) \ \mathrm {[cd]} \ $は，ワンポイント解説「2.水平面照度$ \ E_{\mathrm {h}} \ $」の通り，
\[
\begin{eqnarray}
E_{\mathrm {A}}\left( 0 \right) &=&\frac {I_{\mathrm {A}}\left( 0 \right) }{h^{2}} \\[ 5pt ] I_{\mathrm {A}}\left( 0 \right) &=&E_{\mathrm {A}}\left( 0 \right) h^{2} \\[ 5pt ] &=&500\times 2^{2} \\[ 5pt ] &=&2 \ 000 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ワ
$ \ \mathrm {A} \ $の配光が$ \ I_{\mathrm {A}}\left( \theta \right) =I_{\mathrm {A}}\left( 0 \right) \cos ^{4}\theta \ $であることから，鉛直角$ \ 60° \ $方向の光度$ \ I_{\mathrm {A}}\left( 60 \right) \ $は，
\[
\begin{eqnarray}
I_{\mathrm {A}}\left( 60 \right) &=&I_{\mathrm {A}}\left( 0 \right) \cos ^{4}60° \\[ 5pt ] &=&2 \ 000 \times 0.5^{4} \\[ 5pt ] &=&125 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
鉛直角$ \ 60° \ $方向の$ \ \mathrm {LED} \ $ランプから床面までの距離$ \ r \ \mathrm {[m]} \ $は，
\[
\begin{eqnarray}
r\cos 60° &=&h \\[ 5pt ] r&=&\frac {h}{\cos 60° } \\[ 5pt ] &=&\frac {2}{0.5} \\[ 5pt ] &=&4 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であるから，鉛直角$ \ 60° \ $方向の床面の水平面照度$ \ E_{\mathrm {A}}\left( 60 \right) \ \mathrm {[lx]} \ $は，ワンポイント解説「2.水平面照度$ \ E_{\mathrm {h}} \ $」の通り，
\[
\begin{eqnarray}
E_{\mathrm {A}}\left( 60 \right) &=&\frac {hI_{\mathrm {A}}\left( 60 \right) }{r^{3}} \\[ 5pt ] &=&\frac {2\times 125}{4^{3}} \\[ 5pt ] &≒&3.906　→　3.9 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヨ
$ \ \mathrm {A} \ $と同様に，$ \ \mathrm {B} \ $の$ \ \mathrm {LED} \ $ランプは，その直下の水平面照度が$ \ E_{\mathrm {B}}\left( 0 \right) =300 \ \mathrm {[lx]} \ $及び高さ$ \ h=2 \ \mathrm {[m]} \ $なので，直下方向の光度$ \ I_{\mathrm {B}}\left( 0 \right) \ \mathrm {[cd]} \ $は，ワンポイント解説「2.水平面照度$ \ E_{\mathrm {h}} \ $」の通り，
\[
\begin{eqnarray}
E_{\mathrm {B}}\left( 0 \right) &=&\frac {I_{\mathrm {B}}\left( 0 \right) }{h^{2}} \\[ 5pt ] I_{\mathrm {B}}\left( 0 \right) &=&E_{\mathrm {B}}\left( 0 \right) h^{2} \\[ 5pt ] &=&300\times 2^{2} \\[ 5pt ] &=&1 \ 200 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \mathrm {B} \ $の配光が$ \ I_{\mathrm {B}}\left( \theta \right) =I_{\mathrm {A}}\left( 0 \right) \cos \theta \ $であることから，鉛直角$ \ 60° \ $方向の光度$ \ I_{\mathrm {B}}\left( 60 \right) \ $は，
\[
\begin{eqnarray}
I_{\mathrm {B}}\left( 60 \right) &=&I_{\mathrm {B}}\left( 0 \right) \cos 60° \\[ 5pt ] &=&1 \ 200 \times 0.5 \\[ 5pt ] &=&600 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，鉛直角$ \ 60° \ $方向の床面の水平面照度$ \ E_{\mathrm {B}}\left( 60 \right) \ \mathrm {[lx]} \ $は，ワンポイント解説「2.水平面照度$ \ E_{\mathrm {h}} \ $」の通り，
\[
\begin{eqnarray}
E_{\mathrm {B}}\left( 60 \right) &=&\frac {hI_{\mathrm {B}}\left( 60 \right) }{r^{3}} \\[ 5pt ] &=&\frac {2\times 600}{4^{3}} \\[ 5pt ] &=&18.75　→　18.8 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ル
(3)及び(4)より，水平面照度の比は，
\[
\begin{eqnarray}
\frac {E_{\mathrm {B}}\left( 60 \right) }{E_{\mathrm {A}}\left( 60 \right) }&=&\frac {18.75}{3.906} \\[ 5pt ] &≒&4.80 \\[ 5pt ] \end{eqnarray}
\] と求められる。