【問題】
【難易度】★★★☆☆(普通)
次の文章は,サイリスタ変換器を用いた直流電動機駆動に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
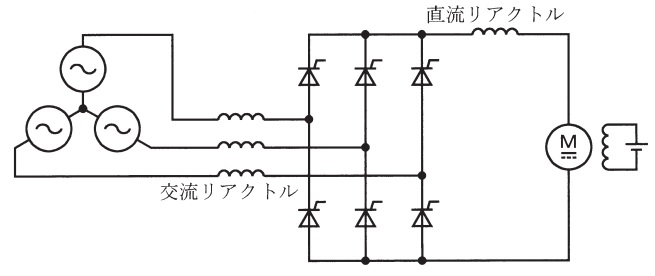
図のようにサイリスタ変換器の直流側に直流機の電機子巻線を接続した直流機駆動システムを\( \ \fbox { (1) } \ \)と呼ぶ。直流他励電動機を用いる場合,サイリスタ変換器の制御遅れ角\( \ \alpha \ \)を操作すると,直流機の\( \ \fbox { (2) } \ \)を制御できる。電機子電流が連続であれば,軽負荷時の\( \ \fbox { (2) } \ \)は,ほぼ\( \ \cos \alpha \ \)に比例する。また,サイリスタがオンしているときの順方向電圧と交流及び直流リアクトルの抵抗が無視できる場合には,\( \ \alpha \ \)を一定としたまま負荷トルクが増加すると,電機子巻線抵抗及び\( \ \fbox { (3) } \ \)の影響によって,負荷トルクにほぼ比例して回転速度は低下する。
図の回路構成の場合,\( \ \alpha \ \)を操作するだけでは,制動トルクを発生することはできない。回生制動を行うためには,\( \ \fbox { (4) } \ \)などが必要になる。\( \ \fbox { (4) } \ \)を行って,直流機を回生制動する場合,サイリスタ変換器の\( \ \alpha \ \)は\( \ \fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 静止レオナード &(ロ)& トルク \\[ 5pt ]
&(ハ)& 電機子巻線の極数切換え &(ニ)& 電機子巻線の自己インダクタンス \\[ 5pt ]
&(ホ)& 界磁電流の方向反転 &(ヘ)& 0 \ [°] \\[ 5pt ]
&(ト)& 電機子電流 &(チ)& 回転速度 \\[ 5pt ]
&(リ)& 交流リアクトル &(ヌ)& 直流リアクトル \\[ 5pt ]
&(ル)& サイリスタセルビウス &(ヲ)& 90 \ [°] \ 未満 \\[ 5pt ]
&(ワ)& 交流電源の相順切換え &(カ)& サイクロコンバータ \\[ 5pt ]
&(ヨ)& 90 \ [°] \ 以上 && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相サイリスタブリッジを利用した直流電動機の駆動に関する問題です。
三相サイリスタブリッジの出力電圧の導出は,\( \ 1 \ \)種の二次試験においては導出できるようにしておく必要がありますが,一次試験においては式は暗記しておくことも必要かと思います。
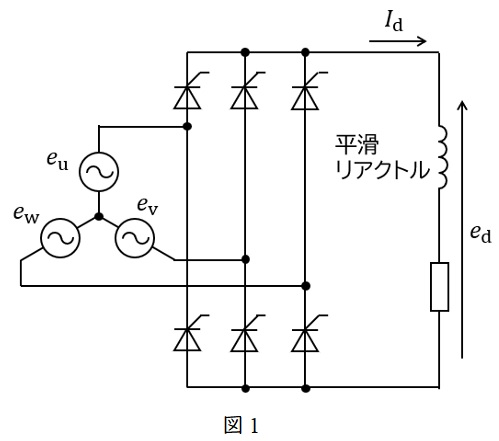
1.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)
図1のような三相サイリスタブリッジ整流回路について考えます。
ただし,電源の電圧は\( \ e_{\mathrm {u}} \ \)を基準として,
\[
\begin{eqnarray}
e_{\mathrm {u}} &=&\sqrt {2}E \sin \theta \\[ 5pt ]
e_{\mathrm {v}} &=&\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
e_{\mathrm {w}} &=&\sqrt {2}E \sin \left( \theta -\frac {4}{3}\pi \right) \\[ 5pt ]
\end{eqnarray}
\]
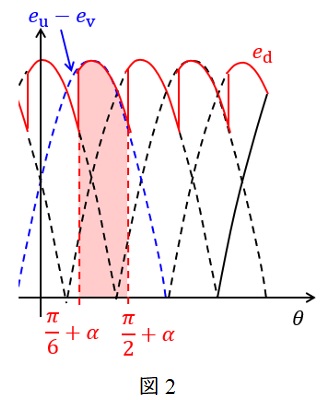
とします。サイリスタの制御角を\( \ \alpha \ \)とすると,出力電圧は図2のようになります。
このとき,出力電圧は周期\( \ \displaystyle \frac {\pi }{3} \ \)で繰り返しているので,その平均出力電圧\( \ E_{\mathrm {d}} \ \)は図2で示した領域の平均値を求めればよいことになります。
図2において,
\[
\begin{eqnarray}
e_{\mathrm {u}} -e_{\mathrm {v}}&=&\sqrt {2}E \sin \theta -\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right)\sin \frac {\pi}{3} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right) \cdot \frac {\sqrt {3}}{2} \\[ 5pt ]
&=&\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので平均出力電圧\( \ E_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left[ \sin \left( \theta -\frac {\pi }{3}\right) \right] _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha } \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left\{ \sin \left( \alpha +\frac {\pi }{6}\right) -\sin \left( \alpha -\frac {\pi }{6}\right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cdot 2\cos \alpha \sin \frac {\pi }{6} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
となります。(和積の公式はこちら)ここで,電源の線間電圧\( \ V \ \)の大きさは相電圧の\( \ \sqrt {3} \ \)倍の大きさなので,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {3\sqrt {2}V}{\pi } \cos \alpha \\[ 5pt ]
&≒&1.35V\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【関連する「電気の神髄」記事】
【解答】
(1)解答:イ
題意より解答候補は,(イ)静止レオナード,(ル)サイリスタセルビウス,(カ)サイクロコンバータ,等になると思います。
本問の問題図のような,サイリスタブリッジ変換器の二次側に直流電動機を接続したシステムは静止レオナードと呼ばれます。
セルビウス方式は巻線形誘導電動機の二次励磁制御の一種,サイクロコンバータは三相電力から単相電力を出力するものとなります。
(2)解答:チ
題意より解答候補は,(ロ)トルク,(ニ)電機子巻線の自己インダクタンス,(ト)電機子電流,(チ)回転速度,等になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)」の通り,サイリスタの制御遅れ角\( \ \alpha \ \)により直流電圧を制御することができます。直流機において,誘導起電力と回転速度は比例するので,\( \ \alpha \ \)により回転速度が制御できることがわかります。
(3)解答:リ
題意より解答候補は,(ニ)電機子巻線の自己インダクタンス,(リ)交流リアクトル,(ヌ)直流リアクトル,等になると思います。
負荷トルクを大きくすると電機子電流が大きくなりますが,これにより直流電動機の電機子巻線抵抗と問題図の交流リアクトルによる電圧降下が大きくなるので,負荷トルクにほぼ比例して回転速度は低下していきます。
(4)解答:ホ
題意より解答候補は,(ハ)電機子巻線の極数切換え,(ホ)界磁電流の方向反転,(ワ)交流電源の相順切換え,になると思います。
回生制動すなわち直流電動機から交流電源に電力を送るためには,サイリスタに順方向電圧をかけなければならないので,直流電動機の電圧の極性を通常時の逆としなければなりません。直流電動機の電圧の極性を逆にするためには界磁電流の方向反転を行えば良いことになります。
(5)解答:ヨ
題意より解答候補は,(ヘ)\( \ 0 \ [°] \ \),(ヲ)\( \ 90 \ [°] \ \)未満,(ヨ)\( \ 90 \ [°] \ \)以上,になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)」の通り,直流電圧を負とするためには,サイリスタの制御遅れ角\( \ \alpha \ \)は\( \ 90 \ [°] \ \)以上とすれば良いことがわかると思います。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん