【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,永久磁石式同期電動機の駆動法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
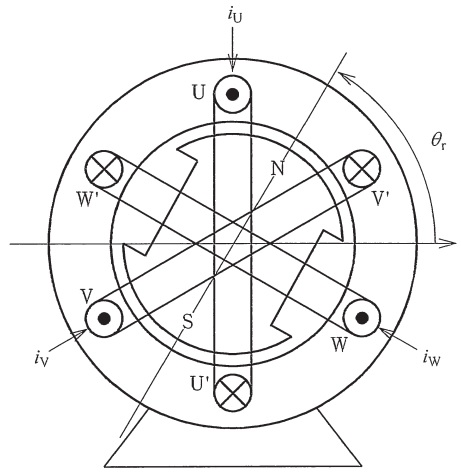
同期電動機の基本的な構成を図に示す。同期電動機を高効率に,かつ,高速応答に可変速駆動するには,\( \ \fbox { (1) } \ \)に応じて固定子電流を制御する方法が用いられる。これは誘導電動機のベクトル制御と原理的に同じである。このような駆動システムにおいて,同期電動機に永久磁石式同期電動機を用いた場合を\( \ \fbox { (2) } \ \)と呼ぶことがある。
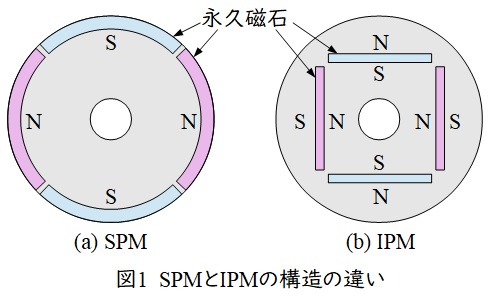
永久磁石式同期電動機でも直軸リアクタンス\( \ X_{\mathrm {d}} \ \)及び横軸リアクタンス\( \ X_{\mathrm {q}} \ \)を定義することができる。永久磁石式同期電動機の構造にはいくつかの種類があり,永久磁石を回転子の表面に貼り付けた\( \ \mathrm {SPM} \ \) (Surface Permanent Magnet) 構造の永久磁石式同期電動機は,永久磁石を回転子内部においた\( \ \mathrm {IPM} \ \) (Interior Permanent Magnet) 構造と比べると,固定子電流による界磁磁束への影響を\( \ \fbox { (3) } \ \)の特徴があり,従来からサーボモータを中心に最も多く使用されている。
インバータを組み合わせた\( \ \mathrm {SPM} \ \)構造の永久磁石式同期電動機駆動システムは,回転子の位置を検出して電流を流し,トルクを発生する。ここで,インバータ及び固定子巻線は三相で,図のような2極機モデルにおいて,\( \ \mathrm {U-U^{\prime }} \ \)の巻線による起磁力の方向に対して回転子の位置を\( \ \theta _{\mathrm {r}} \ \)とすると,固定子トルクの反力である回転子発生トルク\( \ T \ \)は次式となる。
\[
\begin{eqnarray}
T=-K\left[ i_{\mathrm {U}} \mathit {\Phi} _{\mathrm {a}} \sin \theta _{\mathrm {r}} + i_{\mathrm {V}} \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) + i_{\mathrm {W}} \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \right] \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ K \ \)は比例定数,\( \ \mathit {\Phi} _{\mathrm {a}} \ \)は電機子に鎖交する磁束である。各相に正弦波電流
\[
\begin{eqnarray}
i_{\mathrm {U}}=-I_{\mathrm {a}} \sin \theta _{\mathrm {r}} ,i_{\mathrm {V}} = -I _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) ,i_{\mathrm {W}} = -I _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \\[ 5pt ]
\end{eqnarray}
\]
を流すと回転子発生トルクは次式となる。
\[
\begin{eqnarray}
T = \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
同期電動機において,三相固定子電流による起磁力を合成した回転磁界と,回転する界磁極との間の角は,負荷状態によって変化する。この\( \ \mathrm {SPM} \ \)構造の永久磁石式同期電動機駆動システムでは,上記のように絶えず磁極に向かい合う固定子巻線に電流\( \ I_{\mathrm {a}} \ \)を流すように制御しているので,この合成した回転磁界と回転する界磁極との間の角が常に\( \ \fbox { (5) } \ \)され,同じトルクを発生するのにほぼ最小電流で運転できる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 180°に維持 &(ロ)& 強く受けるX_{\mathrm {d}} < X_{\mathrm {q}}の突極機 \\[ 5pt ]
&(ハ)& 回転子の速度 &(ニ)& \frac {3}{2}KI_{\mathrm {a}}\mathit {\Phi} _{\mathrm {a}} \\[ 5pt ]
&(ホ)& ブラシレス\mathrm {DC}モータ &(ヘ)& スイッチトリラクタンスモータ \\[ 5pt ]
&(ト)& \frac {1}{2}KI_{\mathrm {a}}\mathit {\Phi} _{\mathrm {a}} &(チ)& 強く受けるX_{\mathrm {d}} > X_{\mathrm {q}}の突極機 \\[ 5pt ]
&(リ)& \mathrm {DC}モータ &(ヌ)& 界磁の大きさ \\[ 5pt ]
&(ル)& 0°に維持 &(ヲ)& ほぼ無視できる非突極機 \\[ 5pt ]
&(ワ)& 直角に維持 &(カ)& \frac {1}{2}KI_{\mathrm {a}}\mathit {\Phi} _{\mathrm {a}}\cos 2 \theta _{\mathrm {r}} \\[ 5pt ]
&(ヨ)& 界磁極の位置
\end{eqnarray}
\]
【ワンポイント解説】
問題図が全く参考にならず,途中の計算も一次としては計算量が多いため難しい問題であると思います。本問を通じてブラシレスモータの原理や\( \ \mathrm {SPM} \ \)と\( \ \mathrm {IPM} \ \)の違いについて理解しておくようにしておきましょう。
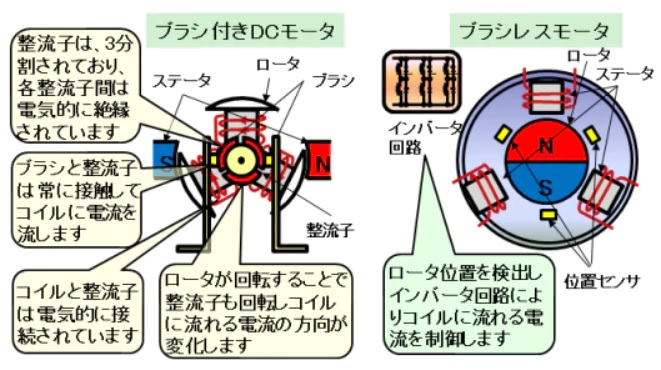
1.ブラシレス\( \ \mathrm {DC} \ \)モータ
\( \ \mathrm {DC} \ \)モータとブラシレス\( \ \mathrm {DC} \ \)モータの構造例は下図の様になります。
\( \ \mathrm {DC} \ \)モータは永久磁石が固定子で電機子巻線が回転する方式が一般的ですが,ブラシレス\( \ \mathrm {DC} \ \)モータは永久磁石が回転する方式が一般的です。
\( \ \mathrm {DC} \ \)モータでは回転する部分と電源との間にブラシと整流子が必要であり,定期的なブラシの交換が必要であるといった保守面での問題があります。一方,ブラシレス\( \ \mathrm {DC} \ \)モータはインバータと磁極センサにより,固定子電流を調整して制御するため,ブラシが不要となります。
出典:東芝デバイス&ストレージ株式会社 HP
https://toshiba.semicon-storage.com/jp/semiconductor/knowledge/e-learning/brushless-motor/chapter2/comparison-brushed-dc-motor-and-brushless-motor.html
2.\( \ \mathrm {SPM} \ \)と\( \ \mathrm {IPM} \ \)の違い
図1(a)のように回転子の表面に永久磁石を張り付けたものを\( \ \mathrm {SPM} \ \) (Surface Permanent Magnet),永久磁石を回転子内部においたものを\( \ \mathrm {IPM} \ \) (Interior Permanent Magnet) と言います。\( \ \mathrm {SPM} \ \)は固定子電流による界磁磁束への影響をほぼ無視できる(どの場所でも固定子電流から永久磁石までの距離が等しいため)特徴があり,ブラシレス\( \ \mathrm {DC} \ \)モータにはよく利用されています。
一方,\( \ \mathrm {IPM} \ \)は,場所により固定子から永久磁石までの等価ギャップが変わるので突極機のような特徴になりますが,永久磁石の固定が容易であり,高速回転も可能であるから,高出力・高効率の運転が可能となります。したがって,ハイブリッド車のモータに利用されています。
3.半角の公式
\(\cos 2\theta =\cos ^{2}\theta -\sin ^{2}\theta \)を利用すると,
\[
\begin{eqnarray}
\cos 2\theta &=&\left( 1-\sin ^{2}\theta \right) -\sin ^{2}\theta \\[ 5pt ]
∴\sin ^{2}\theta &=& \frac {1-\cos 2\theta }{2} \\[ 5pt ]
\cos 2\theta &=&\cos ^{2}\theta -\left( 1-\cos ^{2}\theta \right) \\[ 5pt ]
∴\cos ^{2}\theta &=& \frac {1+\cos 2\theta }{2} \\[ 5pt ]
\end{eqnarray}
\]
の\(2\)公式が求められます。
【解答】
(1)解答:ヨ
題意より,解答候補は(ハ)回転子の速度,(ヌ)界磁の大きさ,(ヨ)界磁極の位置,になると思います。界磁極の位置によって固定子電流を制御するのがブラシレスモータの特徴となります。
(2)解答:ホ
題意より,解答候補は(ホ)ブラシレス\( \ \mathrm {DC} \ \)モータ,(ヘ)スイッチトリラクタンスモータ,(リ)\( \ \mathrm {DC} \ \)モータ,になると思います。ワンポイント解説「1.ブラシレス\( \ \mathrm {DC} \ \)モータ」でも触れていますが,問題文はブラシレス\( \ \mathrm {DC} \ \)モータの説明をしています。
(3)解答:ヲ
題意より,解答候補は(ロ)強く受ける\( \ X_{\mathrm {d}} < X_{\mathrm {q}} \ \)の突極機,(チ)強く受ける\( \ X_{\mathrm {d}} > X_{\mathrm {q}} \ \)の突極機,(ヲ)ほぼ無視できる非突極機,になると思います。ワンポイント解説「2.\( \ \mathrm {SPM} \ \)と\( \ \mathrm {IPM} \ \)の違い」の通り,\( \ \mathrm {SPM} \ \)は固定子電流による界磁磁束への影響をほぼ無視できる非突極機のような特徴を持つようになります。
(4)解答:ニ
題意に沿って,各値を代入し整理すると,
\[
\begin{eqnarray}
T&=&-K\left[ i_{\mathrm {U}} \mathit {\Phi} _{\mathrm {a}} \sin \theta _{\mathrm {r}} + i_{\mathrm {V}} \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) + i_{\mathrm {W}} \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \right] \\[ 5pt ]
&=&-K\left[ -I_{\mathrm {a}} \sin \theta _{\mathrm {r}} \mathit {\Phi} _{\mathrm {a}} \sin \theta _{\mathrm {r}} -I _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) -I _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \mathit {\Phi} _{\mathrm {a}} \sin \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \right] \\[ 5pt ]
&=&K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \left[ \sin ^{2} \theta _{\mathrm {r}} +\sin ^{2} \left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right) +\sin ^{2} \left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right) \right] \\[ 5pt ]
&=&K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \left[ \frac {1-\cos 2\theta _{\mathrm {r}}}{2} +\frac {1-\cos 2\left( \theta _{\mathrm {r}}-\frac {2\pi }{3} \right)}{2} +\frac {1-\cos 2\left( \theta _{\mathrm {r}}-\frac {4\pi }{3} \right)}{2} \right] \\[ 5pt ]
&=&\frac {1}{2}K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \left[ 3-\cos 2\theta _{\mathrm {r}}-\cos \left( 2\theta _{\mathrm {r}}-\frac {4\pi }{3} \right) -\cos \left( 2\theta _{\mathrm {r}}-\frac {8\pi }{3} \right) \right] \\[ 5pt ]
&=&\frac {1}{2}K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \left[ 3-\cos 2\theta _{\mathrm {r}}-\cos 2\theta _{\mathrm {r}}\cos \frac {4\pi }{3}-\sin 2\theta _{\mathrm {r}}\sin \frac {4\pi }{3} -\cos 2\theta _{\mathrm {r}}\cos \frac {8\pi }{3}-\sin 2\theta _{\mathrm {r}}\sin \frac {8\pi }{3} \right] \\[ 5pt ]
&=&\frac {1}{2}K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \left[ 3-\cos 2\theta _{\mathrm {r}}+\frac {1}{2}\cos 2\theta _{\mathrm {r}}+\frac {\sqrt{3}}{2}\sin 2\theta _{\mathrm {r}}+\frac {1}{2}\cos 2\theta _{\mathrm {r}}-\frac {\sqrt{3}}{2}\sin 2\theta _{\mathrm {r}}\right] \\[ 5pt ]
&=&\frac {3}{2}K\mathit {\Phi} _{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ワ
題意より,解答候補は(イ)\( \ 180° \ \)に維持,(ル)\( \ 0° \ \)に維持,(ワ)直角に維持,になると思います。同電流下では回転子の磁界と磁極が直交するように制御することで最大トルクを得られることができるので,直角に維持が正答となります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん