【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,高調波抑制フィルタに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
系統へ流出する高調波電流は上限値を超えないように抑制する必要がある。高調波の次数が低いほど,系統への影響が大きいといわれている。角周波数\( \ \omega \ \)の三相系統では,負荷が平衡している場合,対称性により特定の次数の高調波はごく小さく,一般に,最も大きい高調波は\( \ \fbox { (1) } \ \)高調波となる。
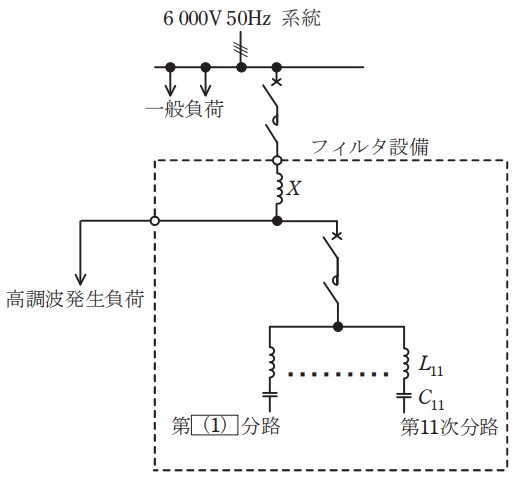
図に示した設備において,\( \ X \ \)で示すリアクトルは\( \ \fbox { (2) } \ \)と呼ばれ,主に構内短絡時の電流を制限することを目的としている。また,高調波を抑制するためのフィルタ設備の各分路は,高調波次数に対応してコンデンサとリアクトルで構成されている。
第\( \ 11 \ \)次高調波に対応するための第\( \ 11 \ \)次分路のフィルタをリアクトルとコンデンサの共振周波数により選定したとしたとき,インダクタンス\( \ L_{11} \ \)とコンデンサの静電容量\( \ C_{11} \ \)は\( \ \fbox { (3) } \ \)の関係にある。今,\( \ 6 \ 000 \ \mathrm {V} \ \),\( \ 50 \ \mathrm {Hz} \ \)の系統電圧で,第\( \ 11 \ \)次分路フィルタの容量が\( \ 100 \ \mathrm {kvar} \ \)としたとき,そのフィルタの基本波に対するリアクタンスは\( \ \fbox { (4) } \ \mathrm {\Omega } \ \)である。このとき,リアクトルのインダクタンス\( \ L_{11} \ \)は\( \ \fbox { (5) } \ \mathrm {mH} \ \)である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{\omega C_{11}}=11\omega L_{11} &(ロ)& 偶数次 &(ハ)& 3.18 \\[ 5pt ]
&(ニ)& 分路リアクトル &(ホ)& \ 6 \ 次 &(ヘ)& 360 \\[ 5pt ]
&(ト)& 限流リアクトル &(チ)& 9.55 &(リ)& 120 \\[ 5pt ]
&(ヌ)& 共通リアクトル &(ル)& \frac {1}{\omega C_{11}}=\omega L_{11} &(ヲ)& 104 \\[ 5pt ]
&(ワ)& \frac {1}{\omega C_{11}}=121\omega L_{11} &(カ)& 207.8 &(ヨ)& \ 5 \ 次 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
高調波の発生と抑制フィルタに関する問題です。
近年は太陽光発電等の分散型電源が増え,半導体素子を扱って系統に連系するものが増えてきているため,高調波に対する対策もとても重要です。
フーリエ級数展開の数学の学習をするとわかります(電験対策として必須ではありません)が,方形波や三角波等の波形にはその波形の対称性から奇数次の高調波を含むものが多く,第\( \ 3 \ \)高調波に関しては変圧器の\( \ \Delta \ \)結線等で還流することができるので,高調波の対策は主に\( \ 5 \ \)次以上の奇数次の高調波に対して行います。
1.コイル,コンデンサのリアクタンス(理論科目)
コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}2\pi f L \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}2\pi f C}\left( \frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。したがって,第\( \ n \ \)次高調波に対するリアクタンス\( \ X_{\mathrm {Ln}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {Cn}} \ \mathrm {[\Omega ]} \ \)は,周波数が\( \ n \ \)倍となるので,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {Ln}}&=&\mathrm {j}2\pi \times nf \times L \\[ 5pt ]
&=&\mathrm {j}n\omega L \\[ 5pt ]
&=&\mathrm {j}n X_{\mathrm {L}} \\[ 5pt ]
-\mathrm {j}X_{\mathrm {Cn}}&=&\frac {1}{\mathrm {j}2\pi \times nf \times C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}n\omega C} \\[ 5pt ]
&=&-\mathrm {j}\frac {X_{\mathrm {C}}}{n} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヨ
題意より解答候補は,(ロ)偶数次,(ホ)\( \ 6 \ \)次,(ヨ)\( \ 5 \ \)次,になると思います。
ワンポイント解説の説明の繰り返しとなりますが,対称性により偶数次の高調波は小さく,第\( \ 3 \ \)調波は還流することができるので,一般に最も大きい高調波は\( \ 5 \ \)次高調波となります。
(2)解答:ト
題意より解答候補は,(ニ)分路リアクトル,(ト)限流リアクトル,(ヌ)共通リアクトル,になると思います。
問題図に示すような主に故障電流を抑制するために直列に接続されるリアクトルを限流リアクトルと言います。リアクトルには,分路リアクトル,直列リアクトル,消弧リアクトル等様々な用途がありますので,忘れてしまった方はテキストで復習しておくようにして下さい。
(3)解答:ワ
題意より解答候補は,(イ)\( \ \displaystyle \frac {1}{\omega C_{11}}=11\omega L_{11} \ \),(ル)\( \ \displaystyle \frac {1}{\omega C_{11}}=\omega L_{11} \ \),(ワ)\( \ \displaystyle \frac {1}{\omega C_{11}}=121\omega L_{11} \ \),になると思います。
ワンポイント解説「1.コイル,コンデンサのリアクタンス(理論科目)」の通り,第\( \ 11 \ \)次分路のフィルタをリアクトルとコンデンサの共振周波数により選定する場合,
\[
\begin{eqnarray}
\frac {1}{2\pi \times 11f \times C_{11}}&=&2\pi \times 11f \times L_{11} \\[ 5pt ]
\frac {1}{11 \omega C_{11}}&=&11\omega L_{11} \\[ 5pt ]
\frac {1}{\omega C_{11}}&=&121\omega L_{11} \\[ 5pt ]
\end{eqnarray}
\]
の関係になります。
(4)解答:ヘ
第\( \ 11 \ \)次分路フィルタの基本波に対するリアクタンスを\( \ X_{11} \ \)とすると,
\[
\begin{eqnarray}
Q&=&3\cdot \frac {\displaystyle \left( \frac {V}{\sqrt {3}}\right) ^{2}}{X_{11}} \\[ 5pt ]
&=&\frac {V^{2}}{X_{11}} \\[ 5pt ]
X_{11}&=&\frac {V^{2}}{Q} \\[ 5pt ]
&=&\frac {6 \ 000^{2}}{100\times 10^{3}} \\[ 5pt ]
&=&360 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
(3),(4)より,
\[
\begin{eqnarray}
X_{11}=\frac {1}{\omega C_{11}}-\omega L_{11}&=&360 \\[ 5pt ]
121\omega L_{11}-\omega L_{11}&=&360 \\[ 5pt ]
120\omega L_{11}&=&360 \\[ 5pt ]
\omega L_{11}&=&3 \\[ 5pt ]
2\pi f L_{11}&=&3 \\[ 5pt ]
L_{11}&=&\frac {3}{2\pi f} \\[ 5pt ]
&=&\frac {3}{2\pi \times 50} \\[ 5pt ]
&≒&0.00955 \ \mathrm {[H]} → 9.55 \ \mathrm {[mH]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん