【問題】
【難易度】★★☆☆☆(やや易しい)
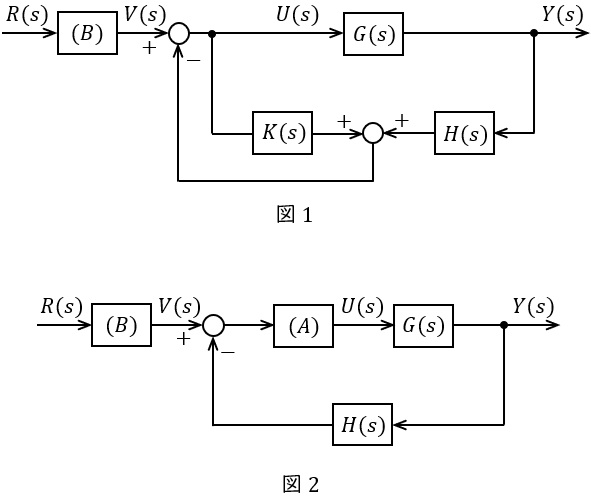
図1のようなフィードバック制御系について,次の問に答えよ。ただし,\( \ R(s) \ \)は目標値,\( \ U(s) \ \)は操作量,\( \ Y(s) \ \)は制御量とする。
(1) 図1のブロック線図を図2のように描き変えたとき,ブロック\( \ \mathrm {(A)} \ \)の伝達関数\( \ G_{A}(s) \ \)を求めよ。
(2) \( \ V(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ W(s) \ \)を求めよ。
(3) \( \ \displaystyle G(s)=\frac {s+1}{s( s+2) } \ \),\( \ \displaystyle K(s)=\frac {k_{0}}{s+10} \ \),\( \ \displaystyle H(s)=\frac {h_{1}s+h_{0}}{s+10} \ \)の場合,\( \ V(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ W(s) \ \)を求め,この分母が,\( \ (s+10)(s^{2} + 10s +50) \ \)となるように,補償器のパラメータ\( \ k_{0} \ \),\( \ h_{1} \ \),\( \ h_{0} \ \)を求めよ。
(4) 上記(3)の結果から,\( \ V(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ W(s) \ \)が,\( \ \displaystyle G(s)=\frac {s+1}{s^{2}+10s+50} \ \)となることを示すことにより,\( \ R(s) \ \)から\( \ Y(s) \ \)までの伝達関数を望ましい伝達関数\( \ \displaystyle T_{d}(s) =\frac {s+20}{s^{2}+10s+50} \ \)に一致させるブロック\( \ \mathrm {(B)} \ \)の伝達関数\( \ G_{B}(s) \ \)を求めよ。
【ワンポイント解説】
フィードバック制御系のブロック線図の等価変換と伝達関数に関する問題です。
(1)のブロック線図の等価変換ができると他の問題は計算力で押し切れる問題かと思います。等価変換は数学の数式のように考えるとわかりやすいです。
1.ブロック線図の考え方
①直列
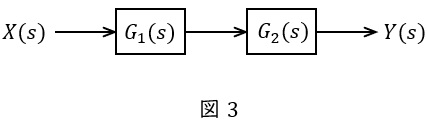
図3のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
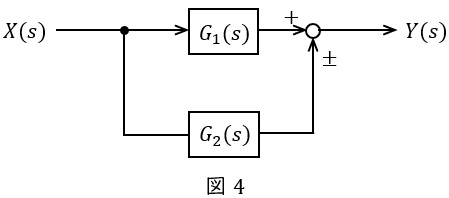
図4のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
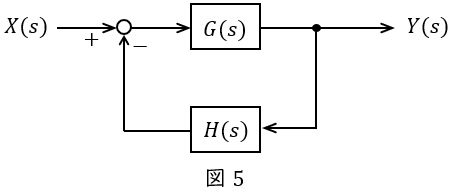
図5のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.ブロック線図の等価変換
やや複雑なブロック線図は点の移動を行うことにより等価変換をします。
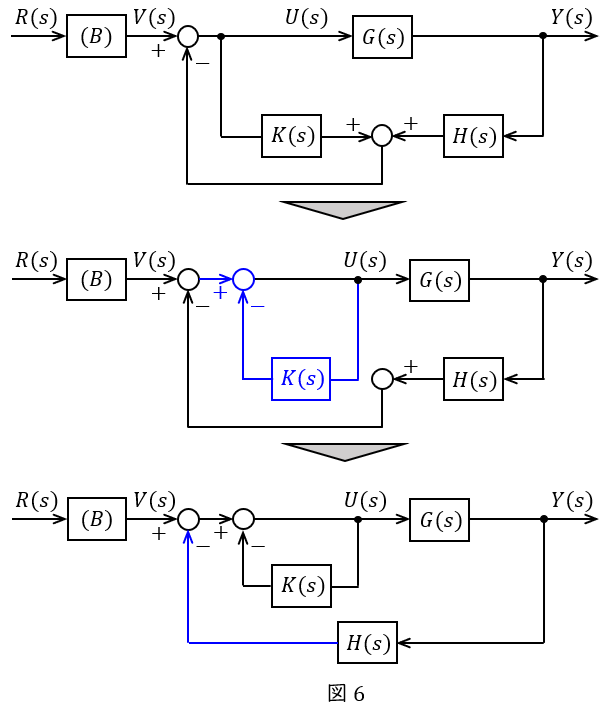
例えば本問のようなブロック線図においては,\( \ K\left( s \right) \ \)を\( \ H\left( s \right) \ \)に加えて\( \ V\left( s \right) \ \)から差し引いても,\( \ K\left( s \right) \ \)を後から差し引いても同じとなるので,図6のように等価変換をすることができます。
【解答】
(1)ブロック\( \ \mathrm {(A)} \ \)の伝達関数\( \ G_{A}(s) \ \)
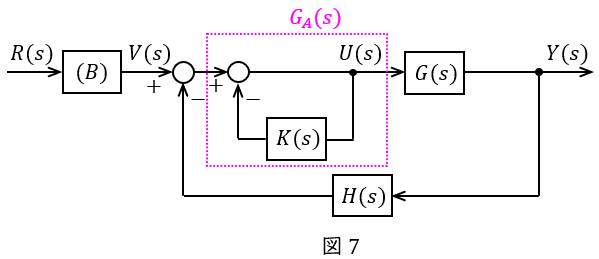
図1のブロック線図を等価変換すると図6のようになり,これを図2と比較すると\( \ G_{A}(s) \ \)は図7に示す箇所となる。
これより\( \ G_{A}(s) \ \)は図5のフィードバック制御系の伝達関数に\( \ G(s)→1 \ \),\( \ H(s)→K(s) \ \)を代入すれば良いので,
\[
\begin{eqnarray}
G_{A}(s)&=&\frac {1}{1+K(s)} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ V(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ W(s) \ \)
(1)と同様に,\( \ W(s) \ \)は図5のフィードバック制御系の伝達関数に\( \ G(s)→G_{A}(s)G(s) \ \),\( \ H(s)→H(s) \ \)を代入すれば良いので,
\[
\begin{eqnarray}
W(s)&=&\frac {G_{A}(s)G(s)}{1+\left\{ G_{A}(s)G(s)\right\}H(s)} \\[ 5pt ]
&=&\frac {\displaystyle \frac {G(s)}{1+K(s)}}{1+\displaystyle \frac {G(s)H(s)}{1+K(s)}} \\[ 5pt ]
&=&\frac {G(s)}{1+K(s)+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)諸条件における\( \ V(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ W(s) \ \)と,分母が\( \ (s+10)(s^{2} + 10s +50) \ \)となるような補償器のパラメータ\( \ k_{0} \ \),\( \ h_{1} \ \),\( \ h_{0} \ \)
(2)解答式に\( \ \displaystyle G(s)=\frac {s+1}{s( s+2) } \ \),\( \ \displaystyle K(s)=\frac {k_{0}}{s+10} \ \),\( \ \displaystyle H(s)=\frac {h_{1}s+h_{0}}{s+10} \ \)を代入すると,
\[
\begin{eqnarray}
W(s)&=&\frac {G(s)}{1+K(s)+G(s)H(s)} \\[ 5pt ]
&=&\frac {\displaystyle \frac {s+1}{s( s+2) }}{\displaystyle 1+\frac {k_{0}}{s+10}+\frac {s+1}{s( s+2) }\cdot \frac {h_{1}s+h_{0}}{s+10}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {s+1}{s( s+2) }}{\displaystyle 1+\frac {k_{0}}{s+10}+\frac {s+1}{s( s+2) }\cdot \frac {h_{1}s+h_{0}}{s+10}}\times \frac {s( s+2) ( s+10) }{s( s+2) ( s+10) } \\[ 5pt ]
&=&\frac {(s+1) ( s+10) }{\displaystyle s( s+2) ( s+10) +k_{0}s( s+2) +(s+1 ) ( h_{1}s+h_{0} )} \\[ 5pt ]
&=&\frac {s^{2}+11s+10 }{s^{3}+12s^{2}+20s +k_{0}s^{2}+2k_{0}s +h_{1}s^{2}+h_{0}s+h_{1}s+h_{0}} \\[ 5pt ]
&=&\frac {s^{2}+11s+10 }{s^{3}+\left( 12+k_{0}+h_{1}\right) s^{2}+\left( 20 +2k_{0}+h_{0}+h_{1}\right) s +h_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,分母が\( \ (s+10)(s^{2} + 10s +50) =s^{3}+20s^{2}+150s+500 \ \)と一致するためには,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
12+k_{0}+h_{1} &=& 20 \\[ 5pt ]
20 +2k_{0}+h_{0}+h_{1} &=& 150 \\[ 5pt ]
h_{0} &=& 500 \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
k_{0}+h_{1} &=& 8 &・・・・・・・・・ ①& \\[ 5pt ]
2k_{0}+h_{0}+h_{1} &=& 130 &・・・・・・・・・ ②& \\[ 5pt ]
h_{0} &=& 500 &・・・・・・・・・ ③& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
を満たす必要がある。
よって,③より,\( \ h_{0} = 500 \ \)と求められ,これを②に代入し整理すれば,
\[
\begin{eqnarray}
2k_{0}+500+h_{1} &=& 130 \\[ 5pt ]
2k_{0}+h_{1} &=& -370 \ ・・・・・・・・・・・ ②^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ②^{\prime }-① \ \)より,\( \ k_{0} = -378 \ \)と求められる。これを\( \ ① \ \)に代入すれば,
\[
\begin{eqnarray}
k_{0}+h_{1} &=& 8 \\[ 5pt ]
-378+h_{1} &=& 8 \\[ 5pt ]
h_{1} &=& 386 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)ブロック\( \ \mathrm {(B)} \ \)の伝達関数\( \ G_{B}(s) \ \)
(3)解答より\( \ W(s) \ \)は,
\[
\begin{eqnarray}
W(s)&=&\frac {(s+1) ( s+10) }{(s+10)(s^{2} + 10s +50) } \\[ 5pt ]
&=&\frac {s+1}{s^{2} + 10s +50 } \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,
\[
\begin{eqnarray}
Y(s)&=&G_{B}(s)W(s)R(s) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,これを\( \ G_{B}(s) \ \)について整理し計算すると,
\[
\begin{eqnarray}
G_{B}(s)&=&\frac {Y(s)}{R(s)}\cdot \frac {1}{W(s)} \\[ 5pt ]
&=&T_{d}(s)\cdot \frac {1}{W(s)} \\[ 5pt ]
&=&\frac {s+20}{s^{2}+10s+50}\cdot \frac {s^{2} + 10s +50 }{s+1} \\[ 5pt ]
&=&\frac {s+20}{s+1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん