【問題】
【難易度】★★☆☆☆(やや易しい)
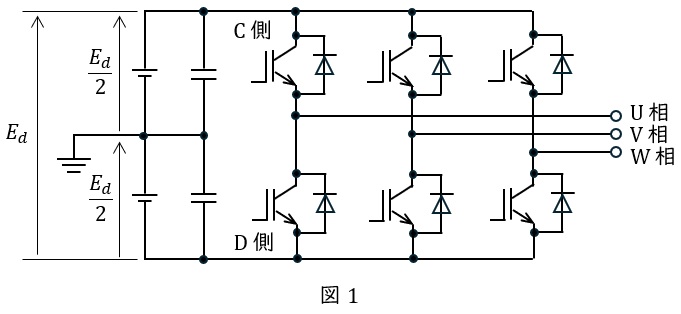
図1に示す回路は,電圧形三相ブリッジ変換器である。オンオフ制御バルブデバイスには\( \ \mathrm {IGBT} \ \)を用いている。この変換器において,\( \ \mathrm {IGBT} \ \)は商用周波数の正弦波信号波と三角波搬送波とを比較してオン・オフを制御している。各相のアーム対それぞれにおいて,各相の信号波瞬時値が搬送波瞬時値よりも大きい場合は\( \ \mathrm {C} \ \)側の\( \ \mathrm {IGBT} \ \)をオンし,\( \ \mathrm {D} \ \)側の\( \ \mathrm {IGBT} \ \)をオフする。逆の場合は\( \ \mathrm {D} \ \)側の\( \ \mathrm {IGBT} \ \)をオンし,\( \ \mathrm {C} \ \)側の\( \ \mathrm {IGBT} \ \)をオフする。搬送波には信号波の周波数の\( \ 3 \ \)倍の周波数の三角波を用いている。この変換器の出力端子にフィルタなどの付属装置を追加して,誘導性の三相負荷に出力する。この変換器の動作について,次の問に答えよ。
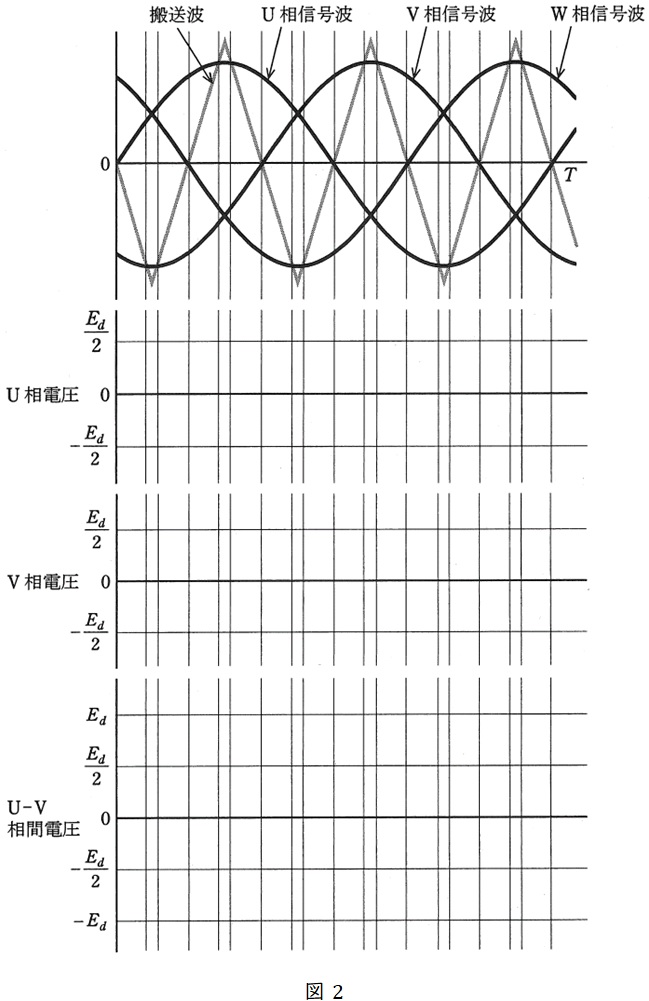
(1) 信号波と搬送波とが図2のような関係になっている。この図と同じ図が答案用紙に印刷されているので,その図に時刻\( \ 0 \ \)から\( \ T \ \)までの期間における,接地点に対する\( \ \mathrm {U} \ \)相及び\( \ \mathrm {V} \ \)相の電圧,並びに\( \ \mathrm {U-V} \ \)相間の電圧の波形を太線で明確に描け。ただし,直流電源電圧の大きさは\( \ E_{d} \ \)であり,直流回路は図1に示すように中点が接地されているものとする。デッドタイムなどのほかの要因を考慮する必要はない。
(2) 図2では,搬送波の周波数が信号波の周波数の\( \ 3 \ \)倍となっている。三相変換器の出力をリアクタンスを介して三相商用系統に連系するとき,搬送波の周波数が低い場合は,その周波数は信号波の周波数の\( \ 3 \ \)倍,\( \ 9 \ \)倍,\( \ 15 \ \)倍,\( \ 21 \ \)倍のように\( \ 3 \ \)の奇数倍とすることが一般的である。\( \ 3 \ \)の倍数とする理由及び奇数倍とする理由をそれぞれ一つずつ記載せよ。
(3) 信号波の周波数の\( \ 3 \ \)倍から\( \ 21 \ \)倍の範囲内で搬送波の周波数を高くしたときのメリット,デメリットをそれぞれ一つずつ記載せよ。
【ワンポイント解説】
三相の\( \ \mathrm {PWM} \ \)インバータに関する問題です。
グラフと論述の問題なので,メカニズムを理解している方は選択すべき問題かと思います。\( \ \mathrm {PWM} \ \)インバータのメカニズム自体はそれほど難解ではありませんので,本問で理解するようにしましょう。
1.三相インバータの動作と出力波形
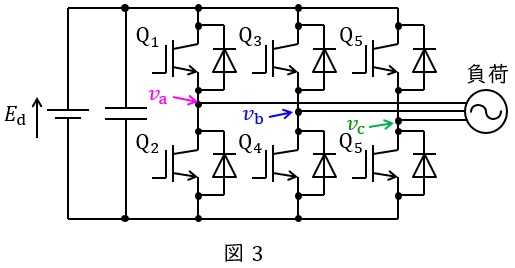
図3に三相インバータ(\( \ 2 \ \)レベル)の回路構成を示します。
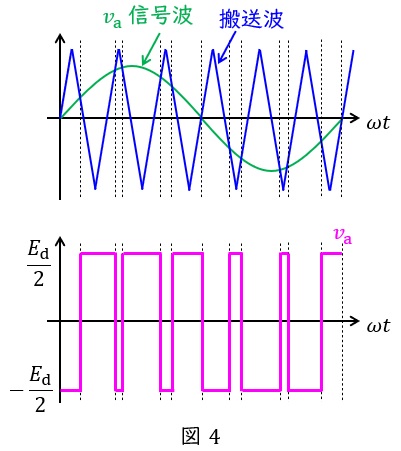
\( \ \mathrm {PWM} \ \)制御では図3において,対になっているスイッチ\( \ \mathrm {Q_{1}} \ \)と\( \ \mathrm {Q_{2}} \ \),\( \ \mathrm {Q_{3}} \ \)と\( \ \mathrm {Q_{4}} \ \),\( \ \mathrm {Q_{5}} \ \)と\( \ \mathrm {Q_{6}} \ \)を図4のように搬送波(三角波)と信号波を大小比較することでオンオフ切換を行い交流出力を得ます。
図4の例においては信号波>搬送波のとき\( \ \mathrm {Q_{1}} \ \)をオン,\( \ \mathrm {Q_{2}} \ \)をオフし,搬送波>信号波のとき\( \ \mathrm {Q_{1}} \ \)をオフ,\( \ \mathrm {Q_{2}} \ \)をオンしてパルス幅により出力電圧を調整しています。
そして,信号波を\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずらして\( \ \mathrm {Q_{3}} \ \)と\( \ \mathrm {Q_{4}} \ \),そして\( \ \mathrm {Q_{5}} \ \)と\( \ \mathrm {Q_{6}} \ \)をオンオフ制御することで出力に三相交流を得ることができます。
【解答】
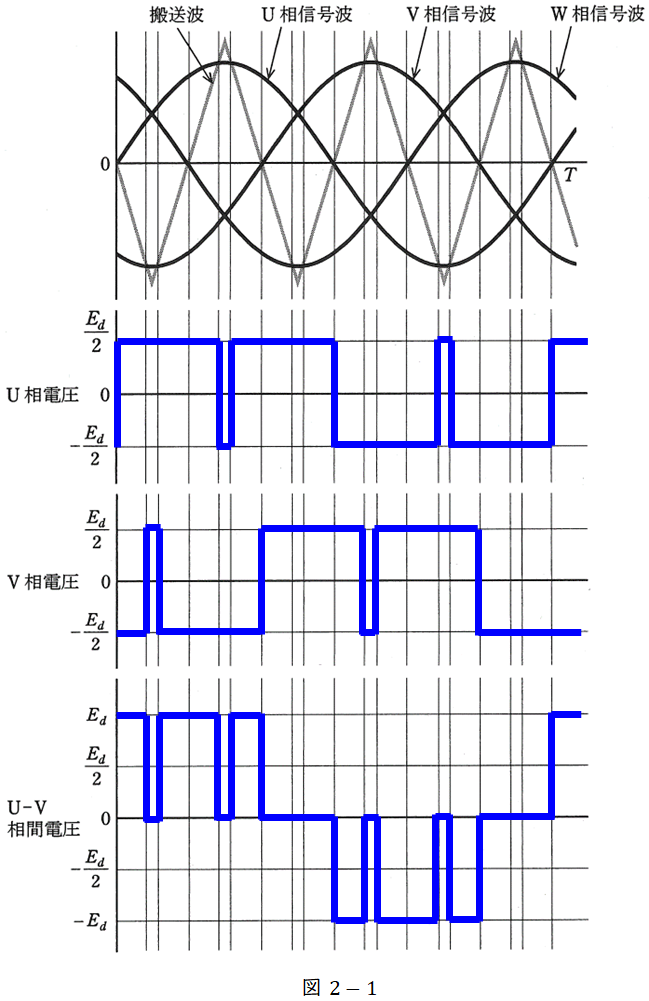
(1)時刻\( \ 0 \ \)から\( \ T \ \)までの期間における,接地点に対する\( \ \mathrm {U} \ \)相及び\( \ \mathrm {V} \ \)相の電圧,並びに\( \ \mathrm {U-V} \ \)相間の電圧の波形
問題文及びワンポイント解説「1.三相インバータの動作と出力波形」の通り,信号波>搬送波のとき\( \ \displaystyle \frac {E_{d}}{2} \ \),搬送波>信号波のとき\( \ \displaystyle -\frac {E_{d}}{2} \ \)を出力するのが\( \ \mathrm {U} \ \)相及び\( \ \mathrm {V} \ \)相の電圧となる。
また,\( \ \mathrm {U-V} \ \)相間の電圧は,グラフ上で\( \ \mathrm {U} \ \)相の電圧から\( \ \mathrm {V} \ \)相の電圧を差し引いた電圧となる。
以上から,解答は図2-1のようになる。
(2)搬送波の周波数が信号波の周波数の\( \ 3 \ \)の倍数とする理由及び奇数倍とする理由
(ポイント)
・\( \ 3 \ \)の倍数とすることで,搬送波と信号波の交差するタイミングを三相全く同じにできます(問題図でいくと必ず零点で三相同じように搬送波と交差しています)。
・図4のように偶数倍とすると波形が線対称になっていない(1番目の山と3番目の山の長さが異なる)ことがわかるかと思います。これにより出力波形を綺麗にすることができません。
(試験センター解答)
下記のような解答が,いずれか\( \ 1 \ \)項目ずつ記載されていればよい。
●\( \ 3 \ \)の倍数とする理由
・三相間で電圧波形を同じにできる。
・相間で\( \ 3 \ \)の倍数次の高調波を相殺し抑制できる。
●奇数倍とする理由
・偶数次高調波の発生を抑制できる。
・正と負の波形を同じにできる。
(3)信号波の周波数の\( \ 3 \ \)倍から\( \ 21 \ \)倍の範囲内で搬送波の周波数を高くしたときのメリット,デメリット
(ポイント)
・周波数を高くすればするほど、より綺麗な\( \ \mathrm {PWM} \ \)波形が描けることがわかるかと思います。
・\( \ \mathrm {IGBT} \ \)のスイッチングが増えるので,損失が増えノイズも発生しやすくなります。
(試験センター解答)
下記のような解答が,いずれか\( \ 1 \ \)項目ずつ記載されていればよい。
●メリット
・電流波形を正弦波に近づけられる。
・フィルタを小形にできる。
●デメリット
・損失が増加する。
・(問題文に記載された搬送波周波数の範囲では)騒音が大きくなりやすい。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん