【問題】
【難易度】★★★★★(難しい)
図1は,三相ブリッジ接続の電圧形自励\( \ \mathrm {IGBT} \ \)インバータ\( \ 2 \ \)台を変圧器で直列に多重接続した\( \ 2 \ \)多重インバータ装置の主回路である。
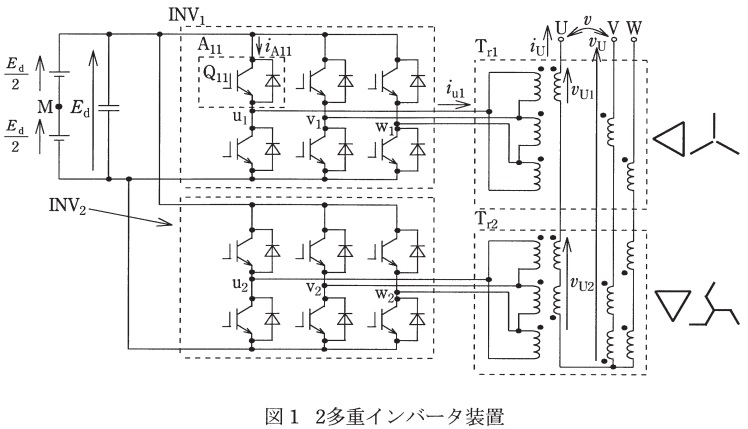
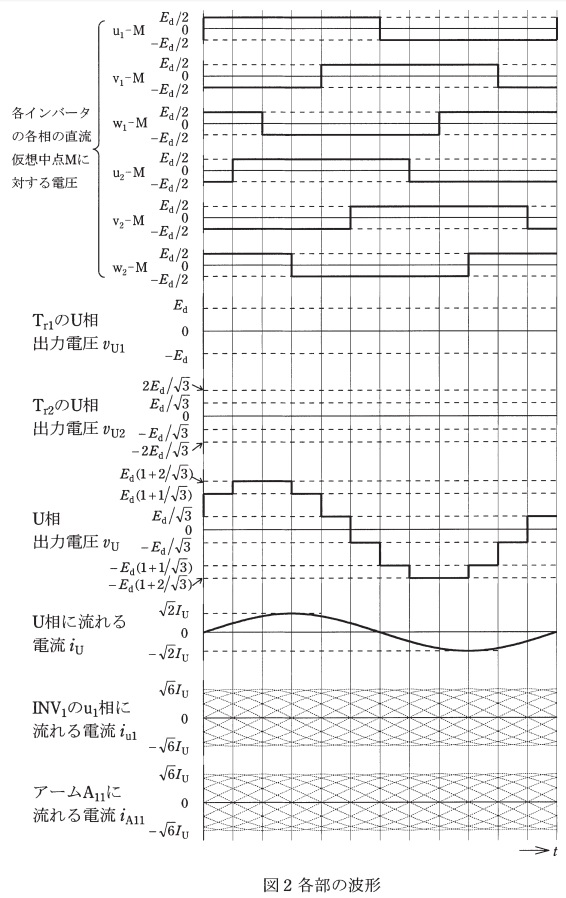
インバータ\( \ \mathrm {INV}_{1} \ \)及び\( \ \mathrm {INV}_{2} \ \)は,直流の仮想中点\( \ \mathrm {M} \ \)に対する各相の電圧波形が図\( \ 2 \ \)のようになって動作している。変換装置用変圧器\( \ \mathrm {T}_{\mathrm {r1}} \ \)は,巻線比が\( \ 1:1 \ \)である。変換装置用変圧器\( \ \mathrm {T}_{\mathrm {r2}} \ \)は,直流側(インバータ側)が\( \ 1 \ \)に対して交流側(出力側)は\( \ \displaystyle \frac {1}{\sqrt{3}} \ \)の巻数比の\( \ 2 \ \)組の巻線を図1に示すように千鳥結線している。次の問に答えよ。
(1) 答案用紙に図2と同じ図が印刷されているので,このときの\( \ \mathrm {T}_{\mathrm {r1}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U1}} \ \)の波形,及び\( \ \mathrm {T}_{\mathrm {r2}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U2}} \ \)の波形を太い線で明確に描け。
(2) 平衡した三相負荷を出力端子に接続したとき,\( \ \mathrm {U} \ \)相には高調波成分を無視して図2に示す電流\( \ i_{\mathrm {U}} \ \)が流れた。答案用紙に図2と同じ図が印刷されているので,このときの\( \ \mathrm {INV}_{1} \ \)の\( \ \mathrm {u}_{1} \ \)相電流\( \ i_{\mathrm {u1}} \ \)の波形,並びに\( \ \mathrm {IGBT} \ \mathrm {Q}_{11} \ \)及びその逆並列ダイオードで構成されたアーム\( \ \mathrm {A}_{11} \ \)に流れる電流\( \ i_{\mathrm {A11}} \ \)の波形を太い線で明確に描け。
(3) \( \ 2 \ \)多重インバータ装置の出力端子における線間出力電圧\( \ v \ \)の基本波実効値\( \ V_{\mathrm {rms}} \ \)を,直流電圧\( \ E_{\mathrm {d}} \ \)を用いて表せ。
【ワンポイント解説】
自宅でゆっくり学習するには良い問題かもしれませんが,試験時間が大変短い中で本問を解くことは非常に非効率であると思います。本問の場合は,ぱっと見て難しそうなので試験本番では他の問題を選択するのが無難と言えるでしょう。
1.フーリエ級数展開
\( \ f( \theta ) \ \)を周期\( \ 2 \pi \ \)の周期関数であるとしたとき,
\[
\begin{eqnarray}
f\left( \theta \right) &=& a_{0}+\displaystyle \sum_{ n = 1 }^{ \infty } \left( a_{n} \cos n\theta + b_{n} \sin n\theta \right) \\[ 5pt ]
a_{0}&=& \frac {1}{2\pi }\int _{0}^{2\pi} f\left( \theta \right) \mathrm {d}\theta \\[ 5pt ]
a_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \cos n\theta \mathrm {d}\theta \\[ 5pt ]
b_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \sin n\theta \mathrm {d}\theta
\end{eqnarray}
\]
とすると,\( \ f( \theta ) \ \)のフーリエ級数展開ができます。
(具体的には設問中の解答で示します。)
2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ 2 \pi \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{2\pi }\int _{0}^{2\pi }f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
②実効値\( \ F \ \)
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
三相電圧形インバータ(2レベルインバータ)
三相多重インバータ(12パルスインバータ)
さまざまな交流波形のフーリエ級数展開まとめ
【解答】
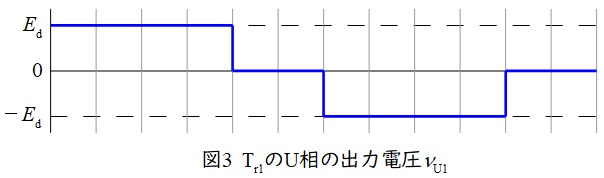
(1)\( \ \mathrm {T}_{\mathrm {r1}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U1}} \ \)の波形,及び\( \ \mathrm {T}_{\mathrm {r2}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U2}} \ \)の波形
図1より,\( \ \mathrm {T}_{\mathrm {r1}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U1}} \ \)は\( \ \mathrm {u}_{1}-\mathrm {v}_{1} \ \)間電圧の二次側の電圧である。また,\( \ \mathrm {T}_{\mathrm {r1}} \ \)の巻数比は\( \ 1 : 1 \ \)であるから,\( \ v_{\mathrm {U1}} \ \)は\( \ \mathrm {u}_{1}-\mathrm {v}_{1} \ \)間電圧と等しくなる。また,
\[
\begin{eqnarray}
\mathrm {u}_{1}-\mathrm {v}_{1}&=&\left( \mathrm {u}_{1}-\mathrm {M}\right) -\left( \mathrm {v}_{1}-\mathrm {M}\right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,図2の各部の波形より\( \ v_{\mathrm {U1}} \ \)の波形は図3のようになる。
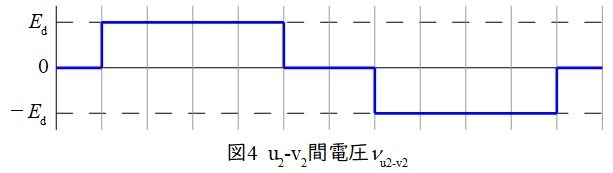
次に,\( \ \mathrm {T}_{\mathrm {r2}} \ \)の\( \ \mathrm {U} \ \)相出力電圧\( \ v_{\mathrm {U2}} \ \)の波形は,極性に注意すると,\( \ \mathrm {u}_{2}-\mathrm {v}_{2} \ \)間電圧と\( \ \mathrm {w}_{2}-\mathrm {v}_{2} \ \)間電圧の和の二次側の電圧である。\( \ \mathrm {u}_{2}-\mathrm {v}_{2} \ \)間電圧と\( \ \mathrm {w}_{2}-\mathrm {v}_{2} \ \)間電圧はそれぞれ図4,図5のように描くことができ,巻数比\( \ \displaystyle 1 : \frac {1}{\sqrt {3}} \ \)であるから,\( \ v_{\mathrm {U2}} \ \)の波形は図6のように描くことができる。


(2)\( \ \mathrm {INV}_{1} \ \)の\( \ \mathrm {u}_{1} \ \)相電流\( \ i_{\mathrm {u1}} \ \)の波形,並びに\( \ \mathrm {IGBT} \ \mathrm {Q}_{11} \ \)及びその逆並列ダイオードで構成されたアーム\( \ \mathrm {A}_{11} \ \)に流れる電流\( \ i_{\mathrm {A11}} \ \)の波形
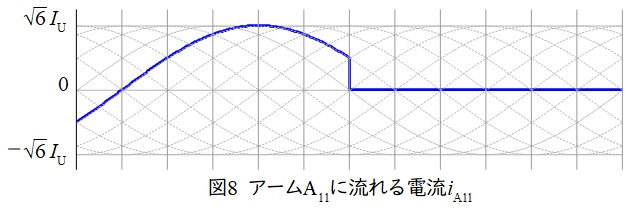
\( \ \mathrm {T}_{\mathrm {r1}} \ \)は\( \ \Delta – \mathrm {Y} \ \)接続され,巻数比が\( \ 1 : 1 \ \)であるので,\( \ i_{\mathrm {u1}} \ \)の波形は\( \ i_{\mathrm {U}} \ \)より位相が\( \ \displaystyle \frac {\pi }{6} \ \)遅れ,波長が\( \ \sqrt {3} \ \)倍の大きさとなる。よって,波形は図7のように描ける。また,アーム\( \ \mathrm {A}_{11} \ \)に電流が流れるのは,\( \ \mathrm {u}_{1}-\mathrm {M} \ \)電圧が正の時なので,波形は図8のように描ける。

(3)線間出力電圧\( \ v \ \)の基本波実効値\( \ V_{\mathrm {rms}} \ \)を,直流電圧\( \ E_{\mathrm {d}} \ \)を用いて表す
\( \ \mathrm {U} \ \)相の出力電圧\( \ v_{\mathrm {U}} \ \)は図2で与えられており,\( \ v_{\mathrm {V}} \ \)は位相が\( \ \displaystyle \frac {2}{3}\pi \ \)遅れた波形となるため,図9の通りとなる。よって,線間出力電圧\( \ v \ \)は\( \ v=v_{\mathrm {U}}-v_{\mathrm {V}} \ \)となるので,図10のように描ける。
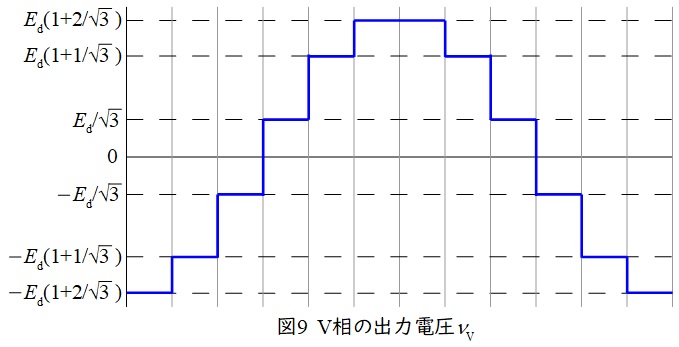
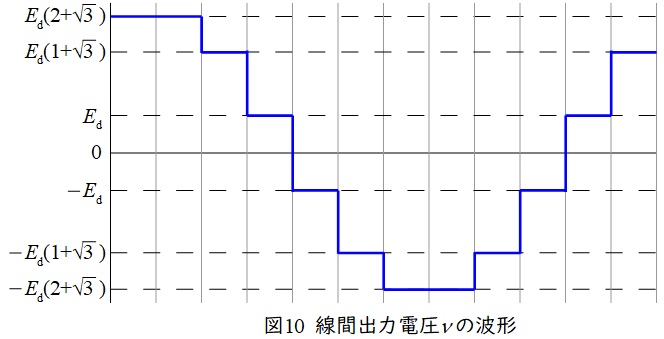
図10より,周期関数の電圧の大きさが\( \ 0 \ \)の点を基準とすると,\( \ \displaystyle 0 ≦ \omega t < \frac {\pi }{2} \ \)においては,
\[
\begin{eqnarray}
v
=
\begin{cases}
E_{\mathrm {d}} & ( \displaystyle 0 ≦ \omega t < \frac {\pi }{6} ) \\[ 5pt ]
E_{\mathrm {d}}\left( 1 +\sqrt {3} \right) & ( \displaystyle \frac {\pi }{6} ≦ \omega t < \frac {\pi }{3} ) \\[ 5pt ]
E_{\mathrm {d}}\left( 2 +\sqrt {3} \right) & ( \displaystyle \frac {\pi }{3} ≦ \omega t < \frac {\pi }{2} ) \\[ 5pt ]
\end{cases}
\end{eqnarray}
\]
となり,ワンポイント解説「1.フーリエ級数展開」より,\( \ v \ \)の基本波を,
\[
\begin{eqnarray}
v&=&a_{0}+a_{1}\cos \theta +b_{1} \sin \theta \\[ 5pt ]
a_{0}&=& \frac {1}{2\pi }\int _{0}^{2\pi} v \mathrm {d}\theta \\[ 5pt ]
a_{1}&=& \frac {1}{\pi }\int _{0}^{2\pi} v \cos \theta \mathrm {d}\theta \\[ 5pt ]
b_{1}&=& \frac {1}{\pi }\int _{0}^{2\pi} v \sin \theta \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
と置くと,\( \ v \ \)は奇関数であるため,\( \ a_{0}=a_{1}=0 \ \)となり,
\[
\begin{eqnarray}
b_{1}&=& \frac {1}{\pi }\int _{0}^{2\pi} v \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {4}{\pi }\int _{0}^{\frac {\pi }{2}} v \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {4}{\pi }\left[ \int _{0}^{\frac {\pi}{6}} E_{\mathrm {d}} \sin \theta \mathrm {d}\theta +\int _{\frac {\pi}{6}}^{\frac {\pi}{3}} E_{\mathrm {d}}\left( 1+\sqrt {3}\right) \sin \theta d\theta + \int _{\frac {\pi}{3}}^{\frac {\pi}{2}} E_{\mathrm {d}}\left( 2+\sqrt {3}\right) \sin \theta \mathrm {d}\theta\right] \\[ 5pt ]
&=& \frac {4}{\pi }E_{\mathrm {d}}\left[ \left[ -\cos \theta \right] _{0}^{\frac {\pi}{6}} +\left( 1+\sqrt {3}\right) \left[ -\cos \theta \right] _{\frac {\pi}{6}}^{\frac {\pi}{3}}+ \left( 2+\sqrt {3}\right) \left[ -\cos \theta \right] _{\frac {\pi}{3}}^{\frac {\pi}{2}}\right] \\[ 5pt ]
&=& \frac {4}{\pi }E_{\mathrm {d}}\left[ \left( -\frac {\sqrt {3}}{2}+1\right) +\left( 1+\sqrt {3}\right) \left( -\frac {1}{2}+\frac {\sqrt{3}}{2}\right) + \left( 2+\sqrt {3}\right) \frac {1}{2}\right] \\[ 5pt ]
&=& \frac {4}{\pi }E_{\mathrm {d}}\left[ \left( -\frac {\sqrt {3}}{2}+1\right) +\left( -\frac {1}{2}+\frac {\sqrt{3}}{2}-\frac {\sqrt{3}}{2}+\frac {3}{2}\right) + \left( 1+\frac {\sqrt {3}}{2}\right) \right] \\[ 5pt ]
&=& \frac {12}{\pi }E_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,\( \ v \ \)の基本波は,
\[
\begin{eqnarray}
v&=&\frac {12}{\pi }E_{\mathrm {d}} \sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,その実効値\( \ V_{\mathrm {rms}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {rms}}&=&\frac {12}{\pi }E_{\mathrm {d}} \cdot \frac {1}{\sqrt {2}} \\[ 5pt ]
&=&\frac {6\sqrt {2}}{\pi }E_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん