【問題】
【難易度】★★★★☆(やや難しい)
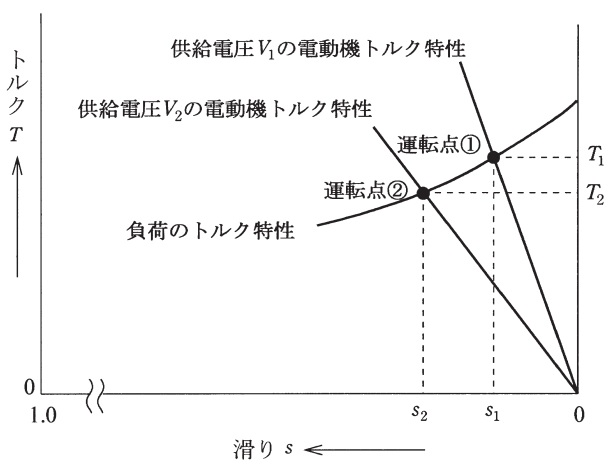
図は,三相かご形誘導電動機に回転速度の2乗に比例するトルクを要求する負荷をかけて運転する場合の,三相かご形誘導電動機と負荷のトルク特性である。
供給電圧を定格電圧\(V_{1}\)として運転する場合,電動機及び負荷のトルク特性の交点,すなわち運転点①における滑り及びトルクは,\(s_{1}\)及び\(T_{1}\)であった。このとき,滑り\(s_{1}\)は\(2.5%\)である。運転中に供給電圧が\(12%\)低下して\(V_{2}\)に変化した場合,滑り\(s_{2}\)及びトルク\(T_{2}\)の運転点②に移ったとする。以下に示す電動機の諸量について,運転点①に対する運転点②の比をそれぞれ求めよ。ただし,電源周波数は一定とし,供給電圧一定の場合,電動機のトルク特性は近似的に直線とみなし,電動機のトルクは滑りに比例するものとする。また,運転点①のとき,鉄損と一次銅損との比は\(3:5\)とし,一次銅損と二次銅損は等しいものとする。
(1) 滑り
(2) 出力
(3) 二次電流
(4) 効率
【ワンポイント解説】
非常に計算力が要求される問題です。一種の機械制御は時間との勝負となるため,例えスムースに解けると思っても本問を選択すべきかどうか疑問が残るところです。
1.誘導電動機のL形等価回路
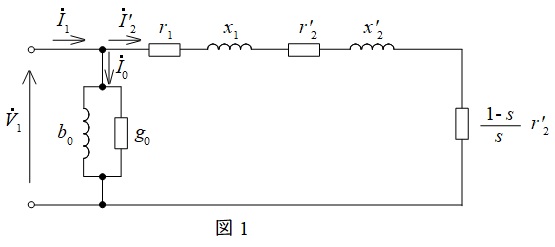
本問では図1のようなL形等価回路が分かっていて,トルクの導出ができる,もしくは分かっていることが前提になっている問題です。L形等価回路は確実に描けるようにしておきましょう。
\[
\begin{eqnarray}
V_{1}&:&一次電圧 \\[ 5pt ]
I_{1}&:&一次電流 \\[ 5pt ]
I_{0}&:&励磁電流 \\[ 5pt ]
I^{\prime}_{2}&:&一次側に換算した二次電流 \\[ 5pt ]
r_{1}&:&一次抵抗 \\[ 5pt ]
x_{1}&:&一次リアクタンス \\[ 5pt ]
r_{2}^{\prime}&:&一次側に換算した二次抵抗 \\[ 5pt ]
x_{2}^{\prime}&:&一次側に換算した二次リアクタンス \\[ 5pt ]
g_{0}&:&励磁コンダクタンス \\[ 5pt ]
b_{0}&:&励磁サセプタンス \\[ 5pt ]
s&:&滑り
\end{eqnarray}
\]
図1より,
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,二次入力\(P_{2}\)は,
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \left\{ {\frac {V_{1}}{\sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right\} ^{2} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\]
となり,発生するトルクは,
\[
\begin{eqnarray}
T&=&\frac {P_{o}}{\omega } \\[ 5pt ]
&=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\(\displaystyle \frac {r_{2}^{\prime}}{s} ≫ r_{1},x_{1},x_{2}\)であるとすると,
\[
\begin{eqnarray}
T&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\left( \frac {r_{2}^{\prime}}{s}\right) ^{2} } \\[ 5pt ]
&=&\frac {3}{\omega _{s}}\cdot \frac {V_{1}^{2}s}{r_{2}^{\prime}} \\[ 5pt ]
\end{eqnarray}
\]
という関係になります。
【解答】
(1)滑り
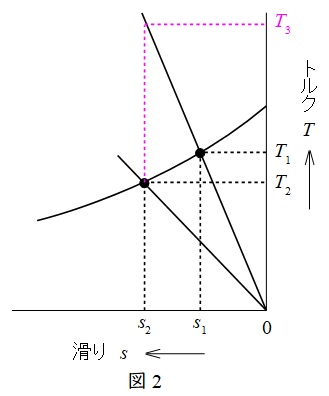
図2の通り,仮想の運転点を設定し,その時のトルクを\(T_{3}\)とすると,トルクは滑りと比例するので,
\[
\begin{eqnarray}
\frac {T_{3}}{T_{1}}&=&\frac {s_{2}}{s_{1}} \\[ 5pt ]
&=&\frac {s_{2}}{0.025} ・・・・・・・①\\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.誘導電動機のL形等価回路」より,トルクは電圧の2乗に比例するので,
\[
\begin{eqnarray}
\frac {T_{2}}{T_{3}}&=&\frac {V_{2}^{2}}{V_{1}^{2}} \\[ 5pt ]
&=&\frac {\left( 1-0.12\right) ^{2}V_{1}^{2}}{V_{1}^{2}} \\[ 5pt ]
&=& 0.7744 ・・・・・・・② \\[ 5pt ]
\end{eqnarray}
\]
となる。また,トルクは回転数の2乗に比例するので,
\[
\begin{eqnarray}
\frac {T_{2}}{T_{1}}&=&\frac {N_{2}^{2}}{N_{1}^{2}} \\[ 5pt ]
&=&\frac {\left( 1-s_{2}\right) ^{2} N_{\mathrm {s}}^{2}}{\left( 1-s_{1}\right) ^{2} N_{\mathrm {s}}^{2}} \\[ 5pt ]
&=& \frac {\left( 1-s_{2}\right) ^{2}}{\left( 1-s_{1}\right) ^{2} } \\[ 5pt ]
&=& \frac {\left( 1-s_{2}\right) ^{2}}{0.975^{2} } ・・・・・・・③ \\[ 5pt ]
\end{eqnarray}
\]
となる。①×②より,
\[
\begin{eqnarray}
\frac {T_{2}}{T_{1}}&=&0.7744\frac {s_{2}}{0.025} \\[ 5pt ]
&≒&30.976s_{2} ・・・・・・・④ \\[ 5pt ]
\end{eqnarray}
\]
③,④より,
\[
\begin{eqnarray}
\frac {\left( 1-s_{2}\right) ^{2}}{\left( 0.975\right) ^{2} }&=&30.976s_{2} \\[ 5pt ]
s_{2}^{2}-31.447s_{2}+1&=&0 \\[ 5pt ]
s_{2}&≒&0.031832,31.415
\end{eqnarray}
\]
と求められ,\(0 < s_{2} < 1\)より,
\[
s_{2}=0.031832
\]
となる。よって,滑りの比は,
\[
\begin{eqnarray}
\frac {s_{2}}{s_{1}}&=&\frac {0.031832}{0.025} \\[ 5pt ]
&≒&1.2733 → 1.27
\end{eqnarray}
\]
と求められる。
(2)出力
\[
\begin{eqnarray}
\frac {P_{\mathrm {o2}}}{P_{\mathrm {o1}}}&=&\frac {\omega _{2}T_{2}}{\omega _{1}T_{1}} \\[ 5pt ]
&=&\frac {\left( 1-s _{2}\right) T_{2}}{\left( 1-s _{1}\right) T_{1}} \\[ 5pt ]
&≒&\frac {0.96817 T_{2}}{0.975 T_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となり,これに③を代入すると,
\[
\begin{eqnarray}
\frac {P_{\mathrm {o2}}}{P_{\mathrm {o1}}}&=&\frac {0.96817 T_{2}}{0.975 T_{1}} \\[ 5pt ]
&=&\frac {0.96817^{3} }{0.975^{3}} \\[ 5pt ]
&=&0.97913 → 0.979 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)二次電流
ワンポイント解説「1.誘導電動機のL形等価回路」より,
\[
\begin{eqnarray}
\frac {P_{\mathrm {o2}}}{P_{\mathrm {o1}}}&=&\frac {3\times \frac {1-s_{2}}{s_{2}}r_{2}^{\prime }{I_{2}}^{2}}{3\times \frac {1-s_{1}}{s_{1}}r_{2}^{\prime }{I_{1}}^{2}} \\[ 5pt ]
&=&\frac {\frac {1-s_{2}}{s_{2}}{I_{2}}^{2}}{\frac {1-s_{1}}{s_{1}}{I_{1}}^{2}} \\[ 5pt ]
0.97913&=&\frac {\frac {1-0.031832}{0.031832}{I_{2}}^{2}}{\frac {1-0.025}{0.025}{I_{1}}^{2}} \\[ 5pt ]
\frac {I_{2}}{I_{1}}&=&1.1205
\end{eqnarray}
\]
と求められる。
(4)効率
電圧変化前後の効率を\(\eta _{1}\),\(\eta _{2}\),鉄損を\(P_{\mathrm {1i}}\),\(P_{\mathrm {2i}}\),一次銅損を\(P_{\mathrm {1c1}}\),\(P_{\mathrm {2c1}}\),二次銅損を\(P_{\mathrm {1c2}}\),\(P_{\mathrm {2c2}}\)とすると,
\[
\begin{eqnarray}
P_{\mathrm {1c1}}=P_{\mathrm {1c2}}&=&\frac {s_{1}}{1-s_{1}}P_{\mathrm {o1}} \\[ 5pt ]
&=&\frac {0.025}{1-0.025}P_{\mathrm {o1}} \\[ 5pt ]
&=&0.025641P_{\mathrm {o1}} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より鉄損は一次銅損の\(\displaystyle \frac {3}{5}\)倍であるから,
\[
\begin{eqnarray}
P_{\mathrm {1i}}&=&\displaystyle \frac {3}{5}P_{\mathrm {1c1}} \\[ 5pt ]
&=&\displaystyle \frac {3}{5}\times 0.025641P_{\mathrm {o1}} \\[ 5pt ]
&≒&0.015385P_{\mathrm {o1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,電圧変化前の効率\(\eta _{1}\)は,
\[
\begin{eqnarray}
\eta _{1}&=&\frac {P_{\mathrm {o1}}}{P_{\mathrm {o1}}+P_{\mathrm {1i}}+P_{\mathrm {1c1}}+P_{\mathrm {1c2}}} \\[ 5pt ]
&=&\frac {P_{\mathrm {o1}}}{P_{\mathrm {o1}}+0.015385P_{\mathrm {o1}}+0.025641P_{\mathrm {o1}}+0.025641P_{\mathrm {o1}}} \\[ 5pt ]
&≒&0.93750 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
ワンポイント解説「1.誘導電動機のL形等価回路」より,鉄損は電圧の2乗に比例,銅損は電流の2乗に比例するので,
\[
\begin{eqnarray}
P_{\mathrm {2i}}&=&\frac {V_{2}^{2}}{V_{1}^{2}}P_{\mathrm {1i}} \\[ 5pt ]
&=&0.88^{2}\times 0.015385P_{1} \\[ 5pt ]
&≒&0.011914 P_{\mathrm {o1}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
P_{\mathrm {2c1}}=P_{\mathrm {2c2}}&=&\frac {I_{2}^{2}}{I_{1}^{2}}P_{\mathrm {1c1}} \\[ 5pt ]
&=&1.1205^{2}\times 0.025641P_{\mathrm {o1}} \\[ 5pt ]
&≒&0.032193 P_{\mathrm {o1}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電圧変化後の効率\(\eta _{2}\)は,
\[
\begin{eqnarray}
\eta _{2}&=&\frac {P_{\mathrm {o2}}}{P_{\mathrm {o2}}+P_{\mathrm {2i}}+P_{\mathrm {2c1}}+P_{\mathrm {2c2}}} \\[ 5pt ]
&=&\frac {0.97913P_{\mathrm {o1}}}{0.97913P_{\mathrm {o1}}+0.011914P_{\mathrm {o1}}+0.032193P_{\mathrm {o1}}+0.032193P_{\mathrm {o1}}} \\[ 5pt ]
&≒&0.92771 \\[ 5pt ]
\end{eqnarray}
\]
となるので電圧変化前後の効率の比は,
\[
\begin{eqnarray}
\frac {\eta _{2}}{\eta _{1}}&=&\frac {0.92771}{0.93750} \\[ 5pt ]
&≒&0.98956 → 0.990 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん