【問題】
【難易度】★★★★★(難しい)
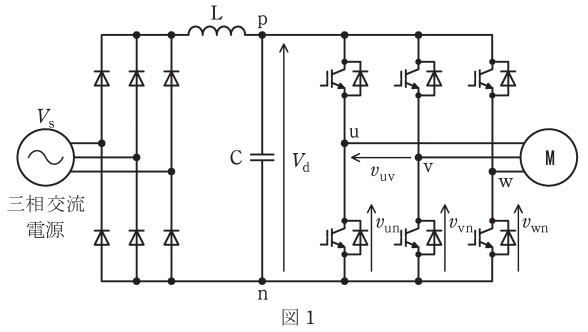
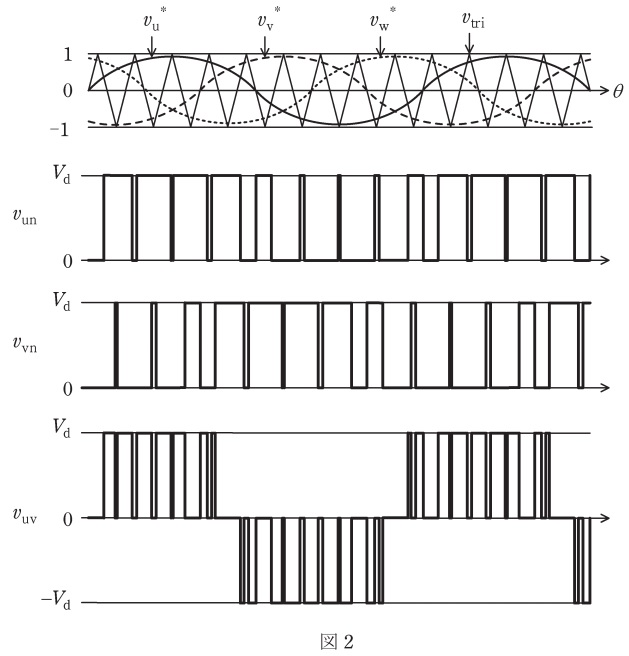
図1は,ダイオード整流器と電圧形インバータを用いた三相誘導電動機可変速駆動システムである。三相交流電源の線間電圧実効値を\( \ V_{\mathrm {s}} \ \)とする。インダクタ\( \ \mathrm {L} \ \)のリプル電流及びコンデンサ\( \ \mathrm {C} \ \)のリプル電圧は無視する。図2は,三角波比較\( \ \mathrm {PWM} \ \)制御を適用した場合の端子\( \ \mathrm {n} \ \)に対する端子\( \ \mathrm {u} \ \),\( \ \mathrm {v} \ \)の電圧\( \ v_{\mathrm {un}} \ \),\( \ v_{\mathrm {vn}} \ \)及び線間電圧\( \ v_{\mathrm {uv}}=v_{\mathrm {un}}-v_{\mathrm {vn}} \ \)の波形である。キャリア波\( \ v_{\mathrm {tri}} \ \)の波高値を\( \ 1 \ \mathrm {V} \ \),線間電圧\( \ v_{\mathrm {uv}} \ \)の基本波実効値を\( \ V_{\mathrm {1uv}} \ \)とする。以下の問に答えよ。必要があれば,\( \ \cos 3 \theta =4\cos ^{3}\theta -3\cos \theta \ \)及び\( \ \sin 3 \theta =3\sin \theta -4\sin ^{3} \theta \ \)を使ってよい。
(1) インバータが停止している場合の直流コンデンサ電圧\( \ V_{\mathrm {d}} \ \)を求めよ。
(2) インバータが動作中の\( \ V_{\mathrm {d}} \ \)を求めよ。
(3) 三角波比較\( \ \mathrm {PWM} \ \)制御の信号波を次式で与える。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
{v_{\mathrm {u}}}^{*}&=& \displaystyle A\sin \theta \\[ 5pt ]
{v_{\mathrm {v}}}^{*}&=& \displaystyle A\sin \left( \theta -\frac {2\pi }{3}\right) ・・・・・・・・・・・・・・ ① \\[ 5pt ]
{v_{\mathrm {w}}}^{*}&=& \displaystyle A\sin \left( \theta +\frac {2\pi }{3}\right) \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
\( \ V_{\mathrm {1uv}} \ \)が\( \ A \ \)に比例する範囲で,\( \ A \ \)を最大としたときの\( \ V_{\mathrm {1uv}} \ \)を\( \ V_{\mathrm {d}} \ \)を使って示せ。
(4) \( \ 3 \ \)次高調波を重畳した信号波を次式で与える。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
{v_{\mathrm {u}}}^{*}&=& \displaystyle A\left( \sin \theta +B\sin 3 \theta \right) \\[ 5pt ]
{v_{\mathrm {v}}}^{*}&=& \displaystyle A\left[ \sin \left( \theta -\frac {2\pi }{3}\right) +B\sin 3 \theta \right] ・・・・・・・・ ② \\[ 5pt ]
{v_{\mathrm {w}}}^{*}&=& \displaystyle A\left[ \sin \left( \theta +\frac {2\pi }{3}\right) +B\sin 3 \theta \right] \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
\( \ \displaystyle B=\frac {1}{6} \ \)とした場合について,信号波\( \ {v_{\mathrm {u}}}^{*} \ \)が\( \ -\pi < \theta < \pi \ \)の範囲で最大となる位相と最大値(波高値)を\( \ A \ \)を使って示せ。
(5) ②式で\( \ \displaystyle B=\frac {1}{6} \ \)とした信号波を用いた場合に,\( \ V_{\mathrm {1uv}} \ \)が\( \ A \ \)に比例する範囲で,\( \ V_{\mathrm {1uv}} \ \)の最大値を\( \ V_{\mathrm {d}} \ \)を使って示せ。
【ワンポイント解説】
三相ダイオード整流器に関する問題は近年非常に増えています。本問はワンポイント解説「1.三相ダイオード整流器のメカニズム」を理解していることが前提となった出題です。難易度が高い問題ですが,過去問にも類題もあり,平成30年度の機械制御では最も計算ミスの可能性が低い問題なので,自信があるなら選択しても良い問題です。
1.三相ダイオード整流器のメカニズム
図3のように三相ダイオード整流器に抵抗負荷が接続されているとします。
問題に合わせ,三相交流電源の線間電圧実効値を\( \ V_{\mathrm {s}} \ \)とすると,相電圧実効値が\( \ \displaystyle \frac {V_{\mathrm {s}}}{\sqrt {3}} \ \)であるから,各相電圧は,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
v_{\mathrm {su}}&=& \displaystyle \frac {\sqrt {2}V_{\mathrm {s}}}{\sqrt {3}}\sin \omega t \\[ 5pt ]
v_{\mathrm {sv}}&=& \displaystyle\frac {\sqrt {2}V_{\mathrm {s}}}{\sqrt {3}}\sin \left( \omega t -\frac {2\pi }{3}\right) \\[ 5pt ]
v_{\mathrm {sw}}&=& \displaystyle\frac {\sqrt {2}V_{\mathrm {s}}}{\sqrt {3}}\sin \left( \omega t -\frac {4\pi }{3}\right) \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
と表すことができます。
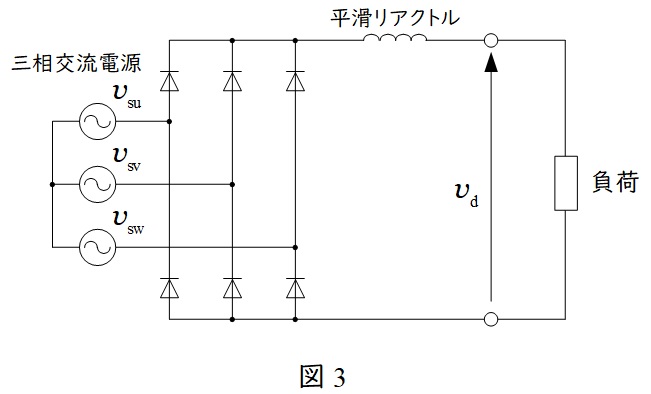
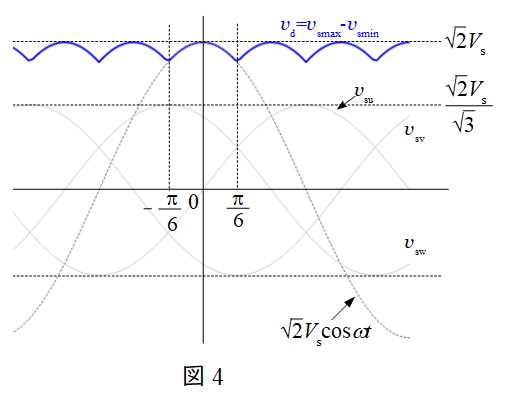
各波形と出力を描いたのが図4です。出力電圧\( \ v_{\mathrm {d}} \ \)は三相交流電源のうちある時点における最大値\( \ v_{\mathrm {smax}} \ \)と最小値\( \ v_{\mathrm {smin}} \ \)の差であるから,波形としては,図4のように描くことができます。出力電圧\( \ v_{\mathrm {d}} \ \)は周期\( \ \displaystyle \frac {\pi }{3} \ \)の青線に示すような波形を描くことになります。
2.平均値と実効値の定義
\(f( \theta )\)を周期\( \ T \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\(F_{\mathrm {av}}\)
\[
F_{\mathrm {av}}=\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta
\]
②実効値\(F\)
\[
F=\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta }
\]
【解答】
(1)インバータが停止している場合の直流コンデンサ電圧\( \ V_{\mathrm {d}} \ \)
インバータが停止している状況では,直流コンデンサ電圧は図4における最大電圧まで上昇することになる。したがって,\( \ \displaystyle V_{\mathrm {d}}=\sqrt{2} V_{\mathrm {s}} \ \)となる。
(2)インバータが動作中の\( \ V_{\mathrm {d}} \ \)
インバータが動作中の\( \ V_{\mathrm {d}} \ \)は図4の青線の波形の平均値である。青線の波形の平均値は\( \ \displaystyle -\frac {\pi }{6} < \omega t < \frac {\pi }{6} \ \)の平均値であるから,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{-\frac {\pi }{6}}^{\frac {\pi }{6}}\sqrt {2}V_{\mathrm {s}}\cos \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {s}}\int _{-\frac {\pi }{6}}^{\frac {\pi }{6}}\cos \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {s}}\left[ \sin \omega t \right] _{-\frac {\pi }{6}}^{\frac {\pi }{6}} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {s}}\left[ \frac {1}{2}-\left( -\frac {1}{2}\right) \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ A \ \)を最大としたときの\( \ V_{\mathrm {1uv}} \ \)を\( \ V_{\mathrm {d}} \ \)を使って示す
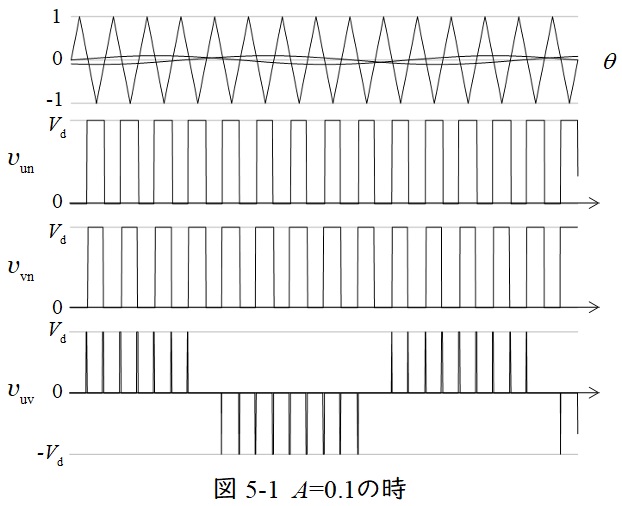
図5-1~5-3に\( \ A=0.1 \ \),\( \ A=0.5 \ \),\( \ A=1.0 \ \)とした時の各波形を示す。図5-1~5-3から分かる通り,\( \ v_{\mathrm {un}} \ \)の基本波の振幅は\( \ A \ \)が大きくなるほど増えていき,\( \ A=1.0 \ \)を超えると,三角波の振幅を超え比例範囲から外れる。その値は\( \ 0<A≦1 \ \)の範囲で\( \ \displaystyle \frac {A}{2}V_{\mathrm {d}} \ \)となる。
よって,\( \ A \ \)を最大すなわち\( \ A=1 \ \)としたときの線間電圧の実効値\( \ V_{\mathrm {1uv}} \ \)は,\( \ \displaystyle V_{\mathrm {1uv}}=\frac {\sqrt {3}}{2\sqrt {2}}V_{\mathrm {d}} \ \)となる。


(4)信号波\( \ {v_{\mathrm {u}}}^{*} \ \)が\( \ -\pi < \theta < \pi \ \)の範囲で最大となる位相と最大値(波高値)を\( \ A \ \)を使って示す
\( \ {v_{\mathrm {u}}}^{*} \ \)の最大値を求めるため,②の\( \ {v_{\mathrm {u}}}^{*} \ \)の式について,両辺微分すると,
\[
\begin{eqnarray}
{v_{\mathrm {u}}}^{*}&=&A\sin \theta +\frac {A}{6}\sin 3 \theta \\[ 5pt ]
\frac {\mathrm {d}{v_{\mathrm {u}}}^{*}}{\mathrm {d}\theta }&=&A\cos \theta +\frac {A}{2}\cos 3 \theta \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle \frac {\mathrm {d}{v_{\mathrm {u}}}^{*}}{\mathrm {d}\theta }=0 \ \)となる\( \ \theta \ \)を求めると,\( \ \cos 3 \theta =4\cos ^{3}\theta -3\cos \theta \ \)であるから,
\[
\begin{eqnarray}
A\cos \theta +\frac {A}{2}\cos 3 \theta &=&0 \\[ 5pt ]
A\cos \theta +\frac {A}{2}\left( 4\cos ^{3}\theta -3\cos \theta \right) &=&0 \\[ 5pt ]
2\cos ^{3}\theta -\frac {1}{2}\cos \theta &=&0 \\[ 5pt ]
\cos \theta \left( 4\cos ^{2}\theta -1\right) &=&0 \\[ 5pt ]
\cos \theta \left( 2\cos \theta +1\right) \left( 2\cos \theta -1\right) &=&0 \\[ 5pt ]
\cos \theta &=&0,±\frac {1}{2} \\[ 5pt ]
\theta &=&-\frac {2\pi }{3},-\frac {\pi }{2},-\frac {\pi }{3},\frac {\pi }{3},\frac {\pi }{2},\frac {2\pi }{3} \\[ 5pt ]
\end{eqnarray}
\]
となる。各\( \ \theta \ \)の値を代入すると,
\[
\begin{eqnarray}
{v_{\mathrm {u}}}^{*}\left( -\frac {2\pi }{3}\right) &=&A\sin \left( -\frac {2\pi }{3}\right) +\frac {A}{6}\sin 3 \left( -\frac {2\pi }{3}\right) \\[ 5pt ]
&=&-\frac {\sqrt {3}}{2}A \\[ 5pt ]
{v_{\mathrm {u}}}^{*}\left( -\frac {\pi }{2}\right) &=&A\sin \left( -\frac {\pi }{2}\right) +\frac {A}{6}\sin 3 \left( -\frac {\pi }{2}\right) \\[ 5pt ]
&=&-\frac {5}{6}A \\[ 5pt ]
{v_{\mathrm {u}}}^{*}\left( -\frac {\pi }{3}\right) &=&A\sin \left( -\frac {\pi }{3}\right) +\frac {A}{6}\sin 3 \left( -\frac {\pi }{3}\right) \\[ 5pt ]
&=&-\frac {\sqrt {3}}{2}A \\[ 5pt ]
{v_{\mathrm {u}}}^{*}\left( \frac {\pi }{3}\right) &=&A\sin \left( \frac {\pi }{3}\right) +\frac {A}{6}\sin 3 \left( \frac {\pi }{3}\right) \\[ 5pt ]
&=&\frac {\sqrt {3}}{2}A \\[ 5pt ]
{v_{\mathrm {u}}}^{*}\left( \frac {\pi }{2}\right) &=&A\sin \left( \frac {\pi }{2}\right) +\frac {A}{6}\sin 3 \left( \frac {\pi }{2}\right) \\[ 5pt ]
&=&\frac {5}{6}A \\[ 5pt ]
{v_{\mathrm {u}}}^{*}\left( \frac {2\pi }{3}\right) &=&A\sin \left( \frac {2\pi }{3}\right) +\frac {A}{6}\sin 3 \left( \frac {2\pi }{3}\right) \\[ 5pt ]
&=&\frac {\sqrt {3}}{2}A \\[ 5pt ]
\end{eqnarray}
\]
となり,最大値となるのは,\( \ \displaystyle \theta =\frac {\pi }{3},\frac {2\pi }{3} \ \)の時で,\( \ \displaystyle \frac {\sqrt {3}}{2}A \ \)である。
\( \ {v_{\mathrm {u}}}^{*} \ \)の波形を描くと図6のようになる。
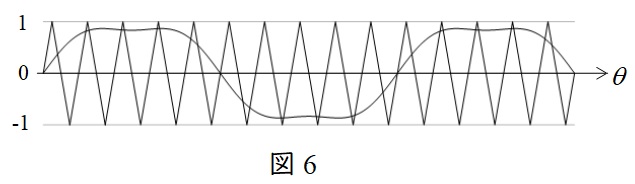
(5)\( \ V_{\mathrm {1uv}} \ \)の最大値を\( \ V_{\mathrm {d}} \ \)を使って示す
\( \ V_{\mathrm {1uv}} \ \)が最大となるためには,\( \ \displaystyle \frac {\sqrt {3}}{2}A=1 \ \)でなくてはならない。したがって,
\[
\begin{eqnarray}
\frac {\sqrt {3}}{2}A&=&1 \\[ 5pt ]
A&=&\frac {2}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
の時最大となり,その実効値は(3)より,
\[
\begin{eqnarray}
V_{\mathrm {1uv}}&=&\frac {\sqrt {3}}{2\sqrt {2}}AV_{\mathrm {d}} \\[ 5pt ]
&=&\frac {\sqrt {3}}{2\sqrt {2}}\times \frac {2}{\sqrt {3}}V_{\mathrm {d}} \\[ 5pt ]
&=&\frac {V_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【本問に関する質疑応答】
電位が\( \ \underline {0 \ \mathrm {V}} \ \)?電圧が\( \ \underline {0 \ \mathrm {V}} \ \)?






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん