【問題】
【難易度】★★★☆☆(普通)
ダイオード整流器,\( \ \mathrm {PWM} \ \)制御インバータ及び誘導電動機からなるドライブシステムがある。滑りによる損失を含めてこのドライブシステムの損失は全て無視するものとして,次の問に答えよ。
(1) トルクが速度の\( \ 2 \ \)乗に比例する特性の負荷及びトルクが速度に関係なく一定の特性の負荷がある。それぞれの負荷に誘導電動機をつないで,\( \ V/f \ \)一定制御のインバータで可変速運転する。ドライブシステムの入力電力を\( \ P_{0} \ \),電動機の回転角速度を\( \ \omega _{0} \ \)とすると,それぞれの負荷の定常特性として,\( \ P_{0} \ \)を\( \ \omega _{0} \ \)と比例定数を用いた式で示せ。
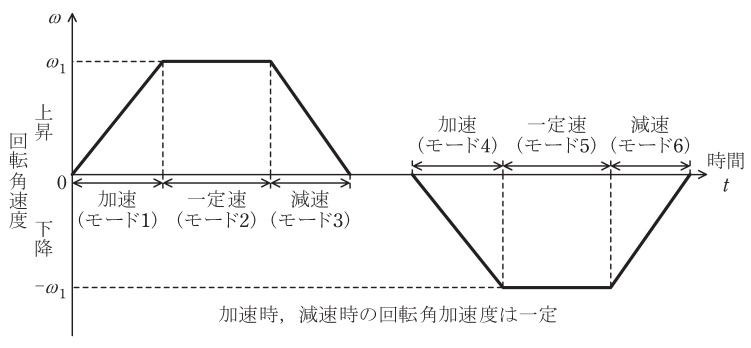
(2) 電動機がある質量の負荷を巻き上げあるいは巻き下げすると,この負荷は電動機の回転方向にかかわらず一方向の定トルク特性負荷である。この電動機をベクトル制御のインバータによって図の速度パターンで可変速運転することを考える。ただし,電動機は,負荷の質量だけを昇降するものとし,その他のトルク及び損失を無視できるものとする。
誘導電動機の入力電力を\( \ P_{1} \ \),誘導電動機の回転軸に換算した機械系の慣性モーメントを\( \ J \ \),この運転の最中の回転角速度を\( \ \omega \left( -\omega _{1}≦\omega ≦\omega _{1}\right) \ \),負荷トルクを\( \ T_{\mathrm {L}} \ \)(一定)とする。\( \ P_{1} \ \)を\( \ J \ \),\( \ \omega \ \)及び\( \ T_{\mathrm {L}} \ \)を用いた式で示せ。ただし,電力\( \ P_{1} \ \)は加減速に要する電力\( \ P_{\mathrm {a}} \ \)と負荷の昇降に要する電力\( \ P_{\mathrm {c}} \ \)の和\( \ P_{\mathrm {a}}+P_{\mathrm {c}} \ \)となる。
(3) 小問(2)において,電動機の運転には図に示す六つの運転モードがある。運転モード\( \ 1~6 \ \)において,電力\( \ P_{\mathrm {a}} \ \),\( \ P_{\mathrm {c}} \ \),\( \ P_{1} \ \)が正となるか負となるか示せ。もし運転モードだけで決まらなければどのような要因によって正となるか負となるかを簡潔に説明せよ。
(4) 小問(3)のような,誘導電動機の入力電力\( \ P_{1} \ \)が負になる運転モードがある場合には,与えられている電力変換器の構成では負の電力を処理できないので,主回路及びその制御方法に追加又は変更が必要である。その例を一つ挙げて,その動作を簡潔に説明せよ。
【ワンポイント解説】
誘導電動機と複合となっていたり,論述問題が入っていたり,いつもの電験の問題とは少し毛色の違う電動機応用に極めて近いパワーエレクトロニクスの問題となっています。(電動機応用は二次試験の範囲に入っていません。)ある意味1種らしい問題ともいえるでしょう。
1.電力\( \ P \ \)とトルク\( \ T \ \)の関係
発電機や電動機が角速度\( \ \omega \ \)で運転している時,電力\( \ P \ \)とトルク\( \ T \ \)の関係は,
\[
\begin{eqnarray}
P &=& \omega T \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.慣性モーメント\( \ J \ \)とトルク\( \ T \ \)の関係
発電機や電動機の慣性モーメントが\( \ J \ \)である時,角速度\( \ \omega \ \)とトルク\( \ T \ \)の関係は,
\[
\begin{eqnarray}
T &=& J\frac {\mathrm {d}\omega }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)トルクが速度の\( \ 2 \ \)乗に比例する特性の負荷及びトルクが速度に関係なく一定の特性の負荷の定常特性として,\( \ P_{0} \ \)を\( \ \omega _{0} \ \)と比例定数を用いた式
トルクが速度の\( \ 2 \ \)乗に比例する特性の負荷の比例定数を\( \ k_{1} \ \),トルクが速度に関係なく一定の特性の負荷の比例定数を\( \ k_{2} \ \)とすると,
\[
\begin{eqnarray}
T_{1}&=&k_{1}\omega _{0}^{2} \\[ 5pt ]
T_{2}&=&k_{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P=\omega T \ \)の関係があるから,
\[
\begin{eqnarray}
P_{0}&=&k_{1}\omega _{0}^{3} \\[ 5pt ]
P_{0}&=&k_{2}\omega _{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ P_{1} \ \)を\( \ J \ \),\( \ \omega \ \)及び\( \ T_{\mathrm {L}} \ \)を用いた式で示す
電動機のトルク\( \ T_{3} \ \)は加速減トルクと定トルクの和であるため,
\[
\begin{eqnarray}
T_{3}&=&J\frac {\mathrm {d}\omega }{\mathrm {d}t}+T_{\mathrm {L}} \\[ 5pt ]
\end{eqnarray}
\]
となり,入力電力\( \ P_{1} \ \)は,
\[
\begin{eqnarray}
P_{1}&=&\omega T_{3} \\[ 5pt ]
&=&\omega \left( J\frac {\mathrm {d}\omega }{\mathrm {d}t}+T_{\mathrm {L}}\right) \\[ 5pt ]
\end{eqnarray}
\]
(3)運転モード\( \ 1~6 \ \)において,電力\( \ P_{\mathrm {a}} \ \),\( \ P_{\mathrm {c}} \ \),\( \ P_{1} \ \)が正となるか負となるか示す
(2)の解答式より,
\[
\begin{eqnarray}
P_{\mathrm {a}}+P_{\mathrm {c}}&=&\omega \left( J\frac {\mathrm {d}\omega }{\mathrm {d}t}+T_{\mathrm {L}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,加速の時\( \ P_{\mathrm {a}}>0 \ \),減速の時\( \ P_{\mathrm {a}}<0 \ \),上昇の時\( \ P_{\mathrm {c}}>0 \ \),下降の時\( \ P_{\mathrm {c}}<0 \ \)となる。また,\( \ P_{1}=P_{\mathrm {a}}+P_{\mathrm {c}} \ \)を考えれば良い。
モード1:
加速+上昇なので,\( \ P_{\mathrm {a}}>0 \ \),\( \ P_{\mathrm {c}}>0 \ \),\( \ P_{1}>0 \ \)
モード2:
一定速+上昇なので,\( \ P_{\mathrm {a}}=0 \ \),\( \ P_{\mathrm {c}}>0 \ \),\( \ P_{1}>0 \ \)
モード3:
減速+上昇なので,\( \ P_{\mathrm {a}}<0 \ \),\( \ P_{\mathrm {c}}>0 \ \),\( \ P_{1} \ \)は正負両方の可能性あり
モード4:
加速+下降なので,\( \ P_{\mathrm {a}}>0 \ \),\( \ P_{\mathrm {c}}<0 \ \),\( \ P_{1} \ \)は正負両方の可能性あり
モード5:
一定速+下降なので,\( \ P_{\mathrm {a}}=0 \ \),\( \ P_{\mathrm {c}}<0 \ \),\( \ P_{1}<0 \ \)
モード6:
減速+下降なので,\( \ P_{\mathrm {a}}<0 \ \),\( \ P_{\mathrm {c}}<0 \ \),\( \ P_{1}<0 \ \)
(4)誘導電動機の入力電力\( \ P_{1} \ \)が負になる運転モードがある場合には,与えられている電力変換器の構成では負の電力を処理できないので主回路及びその制御方法に追加又は変更が必要である。その例を一つ挙げて,その動作を簡潔に説明
(ポイント)
・一番ピンとくるのは自動車等と同じ充電池(二次電池)を使用した運転になると思います。
(試験センター解答例)
ダイオード整流器を使用するのであれば,直流回路に電力を消費する抵抗とその電流を制御するスイッチを設け,直流電圧が過大にならないようスイッチをオンオフ制御する発電運転を行う。あるいは,直流回路からチョッパを介して二次電池を接続し,直流電圧が過大にならないように電池の充放電制御を行う。あるいは,ダイオード整流器を回生用 PWM コンバータに置き換え,直流電圧が一定になるように PWM コンバータで電圧制御を行う。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん