《機械・制御》〈パワーエレクトロニクス〉[R02:問3]直流－直流変換回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

高周波スイッチング直流－直流変換回路のリプルに関して，次の問に答えよ。

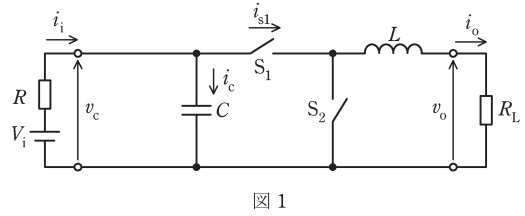
図1に定電圧源\( \ V_{\mathrm {i}} \ \)と内部抵抗\( \ R \ \)からなる電源を入力とし，抵抗\( \ R_{\mathrm {L}} \ \)を負荷とした高周波スイッチング直流－直流変換回路を示す。スイッチ\( \ \mathrm {S}_{\mathrm {1}} \ \)の通流率を\( \ D \ \)とし，スイッチ\( \ \mathrm {S}_{\mathrm {1}} \ \)と\( \ \mathrm {S}_{\mathrm {2}} \ \)はスイッチング周期\( \ T \ \)の間にそれぞれ\( \ DT \ \)と\( \ \left( 1-D\right) T \ \)の期間に相補的に導通し，通流率\( \ D \ \)を調整して，出力電圧\( \ v_{\mathrm {o}} \ \)及び出力電流\( \ i_{\mathrm {o}} \ \)の平均値\( \ V_{\mathrm {o}} \ \)と\( \ I_{\mathrm {o}} \ \)を制御することができる。ただし，これらのスイッチは理想的であり，エネルギー損失なしに瞬時にオンとオフが切り換わるものとする。入力電流\( \ i_{\mathrm {i}} \ \)と並列コンデンサ電流\( \ i_{\mathrm {c}} \ \)は図中の向きとする。回路はある\( \ D \ \)において連続的な繰返し状態，すなわち周期定常状態にあるとする。

今，簡単のために直列リアクトル\( \ L \ \)が十分大きいとして，出力電流\( \ i_{\mathrm {o}}=I_{\mathrm {o}} \ \)が一定であるとするとき，電源のリプルについて以下の問に答えよ。以下では，リプルを表す交流成分の表記に記号\( \ \left( \ {}^{\prime } \ \right) \ \)を用いる。

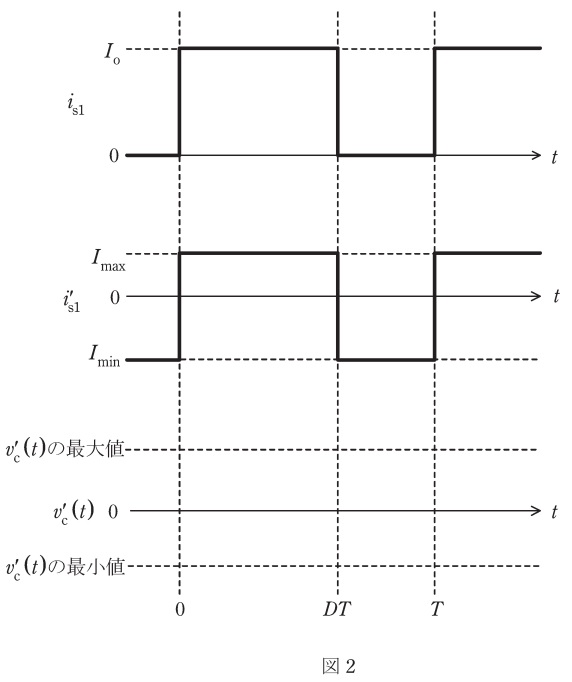
(1)　図2にスイッチ\( \ \mathrm {S}_{\mathrm {1}} \ \)を流れる電流\( \ i_{\mathrm {s1}} \ \)，及びその交流成分\( \ i_{\mathrm {s1}}^{\prime } \ \)の波形を示す。

　a.電流\( \ i_{\mathrm {s1}} \ \)の平均値\( \ I_{\mathrm {s1}} \ \)を求めよ。

　b.交流成分\( \ i_{\mathrm {s1}}^{\prime } \ \)の最大値\( \ I_{\mathrm {max}} \ \)と最小値\( \ I_{\mathrm {min}} \ \)を求めよ。

(2)　並列コンデンサ\( \ C \ \)の電圧\( \ v_{\mathrm {c}} \ \)の交流成分\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)について考える。交流成分\( \ i_{\mathrm {s1}}^{\prime } \ \)に対して電圧源\( \ V_{\mathrm {i}} \ \)は短絡とみなせるので，交流成分\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)について次式の微分方程式が成り立つ。
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) +RC\frac {\mathrm {d}v_{\mathrm {c}}^{\prime }\left( t \right) }{\mathrm {d}t} =-Ri_{\mathrm {s1}}^{\prime }\left( t \right) =
\begin{cases}
-RI_{\mathrm {max}} & \left( 0≦t＜DT \right) \\
-RI_{\mathrm {min}} & \left( DT≦t＜T \right) \\
\end{cases}
\end{eqnarray}
\]

　a.答案用紙に図2と同じ図が印刷されているので，\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)の概略図を描け。

　b.交流成分\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)の波形が三角波で近似することができる条件を示せ。

　c.三角波として近似したときのリプル幅\( \ \Delta v_{\mathrm {c}}^{\prime } \ \)は\( \ I_{\mathrm {o}} \ \)に比例し，\( \ \Delta v_{\mathrm {c}}^{\prime }=kI_{\mathrm {o}} \ \)と表すことができる。比例係数\( \ k \ \)を求めよ。

【ワンポイント解説】

ぱっと見た感じは直流チョッパの降圧チョッパのような回路で易しそうな問題ですが，中身は交流成分を中心とした微分方程式を解く問題や，マクローリン展開の知識を問う問題となっています。
マクローリン展開は\( \ 2 \ \)種までの問題ではまず出題されない問題ですし，近似式は与えられても良い気がしますが，一度理解してしまえばそれほど難しい公式ではないので，マクローリン展開は覚えてしまいましょう。

1.平均値及び実効値
関数\( \ f\left( \theta \right) \ \)の平均値\( \ F_{\mathrm {av}} \ \)及び実効値\( \ F_{\mathrm {e}} \ \)は以下のように求められます。いずれも定義なので覚える必要があります。
①平均値
\[
\begin{eqnarray}
F_{\mathrm {av}} &=& \frac {1}{T}\int ^{T}_{0} f\left( \theta \right) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\]

②実効値
\[
\begin{eqnarray}
F_{\mathrm {e}} &=& \sqrt {\frac {1}{T} \int ^{T}_{0}f\left( \theta \right) ^{2}\mathrm {d}\theta } \\[ 5pt ] \end{eqnarray}
\]

2.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし，抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \)，リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \)，コンデンサ\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると，
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ] v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となります。微分と積分は逆の関係があるので，各電圧から電流\( \ i \ \)を求める式は，
\[
\begin{eqnarray}
i &=& \frac {v_{\mathrm{R}}}{R} \\[ 5pt ] i &=& \frac {1}{L}\int v_{\mathrm{L}} \mathrm {d}t \\[ 5pt ] i &=& C\frac {\mathrm {d}v_{\mathrm{C}}}{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] となります。

3.過渡現象における定常解と過渡解
ⅰ．定常解を\( \ i_{\mathrm {s}} \ \)，過渡解を\( \ i_{\mathrm {t}} \ \)とすると，一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ．定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ．過渡解はスイッチを入れた直後の解すなわち\( \ L \ \)開放(\( \ E=0 \ \)と同義)の時の解です。
これは，電圧に関しても同様に扱うことができます。

4.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x}　\\[ 5pt ] \end{eqnarray}
\] ②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right)　\\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] となった場合，両辺とも対数を外すと，
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=e^{C}\right) \\[ 5pt ] \end{eqnarray}
\] となります。

5.マクローリン展開
無限回微分できる関数\( \ f\left( x \right) \ \)（例えば\( \ \mathrm {e}^{x} \ \)や\( \ \cos x \ \)，\( \ \sin x \ \)等）に関して，以下の式が成立します。
\[
\begin{eqnarray}
f\left( x \right) &=&f\left( 0 \right) +f^{\prime }\left( 0 \right) x+\frac {f^{\prime \prime }\left( 0 \right) }{2!}x^{2}+\frac {f^{\prime \prime \prime }\left( 0 \right) }{3!}x^{3}+\cdots \\[ 5pt ] \end{eqnarray}
\] したがって，\( \ \mathrm {e}^{x} \ \)であれば以下のように展開できます。
\[
\begin{eqnarray}
\mathrm {e}^{x} &=&1 + x+\frac {1}{2!}x^{2}+\frac {1}{3!}x^{3}+\cdots \\[ 5pt ] \end{eqnarray}
\]

※　このような数学を覚えるとオイラーの公式\( \ \mathrm {e}^{\mathrm {j}x} = \cos x +\mathrm {j}\sin x \ \)も導き出せるようになります。興味のある方は微分積分の勉強をしてみて下さい。

【解答】

(1)a.電流\( \ i_{\mathrm {s1}} \ \)の平均値\( \ I_{\mathrm {s1}} \ \)
図2における電流\( \ i_{\mathrm {s1}} \ \)の平均値\( \ I_{\mathrm {s1}} \ \)は，ワンポイント解説「1.平均値及び実効値」より，
\[
\begin{eqnarray}
I_{\mathrm {s1}} &=& \frac {1}{T}\int ^{T}_{0} i_{\mathrm {s1}} \mathrm {d}t \\[ 5pt ] &=& \frac {1}{T}\int ^{DT}_{0} I_{\mathrm {o}} \mathrm {d}t \\[ 5pt ] &=& \frac {I_{\mathrm {o}}}{T}\int ^{DT}_{0} \mathrm {d}t \\[ 5pt ] &=& \frac {I_{\mathrm {o}}}{T}\left[ t\right] ^{DT}_{0} \\[ 5pt ] &=& \frac {I_{\mathrm {o}}}{T}\left( DT-0\right) \\[ 5pt ] &=& DI_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(1)b.交流成分\( \ i_{\mathrm {s1}}^{\prime } \ \)の最大値\( \ I_{\mathrm {max}} \ \)と最小値\( \ I_{\mathrm {min}} \ \)
交流成分\( \ i_{\mathrm {s1}}^{\prime } \ \)の平均値は零であるから，
\[
\begin{eqnarray}
\frac {1}{T}\int ^{T}_{0} i_{\mathrm {s1}}^{\prime } \mathrm {d}t &=& 0 \\[ 5pt ] \int ^{T}_{0} i_{\mathrm {s1}}^{\prime } \mathrm {d}t &=& 0 \\[ 5pt ] \int ^{DT}_{0} I_{\mathrm {max}} \mathrm {d}t+\int ^{T}_{DT} I_{\mathrm {min}} \mathrm {d}t &=& 0 \\[ 5pt ] I_{\mathrm {max}} \left[ t\right] ^{DT}_{0}+I_{\mathrm {min}} \left[ t\right] ^{T}_{DT} &=& 0 \\[ 5pt ] DTI_{\mathrm {max}} +\left( T-DT\right) I_{\mathrm {min}} &=& 0 \\[ 5pt ] DI_{\mathrm {max}} +\left( 1-D\right) I_{\mathrm {min}} &=& 0 \\[ 5pt ] \end{eqnarray}
\] となる。\( \ I_{\mathrm {max}}-I_{\mathrm {min}}=I_{\mathrm {o}} \ \)より，
\[
\begin{eqnarray}
DI_{\mathrm {max}} +\left( 1-D\right) \left( I_{\mathrm {max}}-I_{\mathrm {o}}\right) &=& 0 \\[ 5pt ] DI_{\mathrm {max}} +\left( 1-D\right) I_{\mathrm {max}}-\left( 1-D\right) I_{\mathrm {o}} &=& 0 \\[ 5pt ] I_{\mathrm {max}}-\left( 1-D\right) I_{\mathrm {o}} &=& 0 \\[ 5pt ] I_{\mathrm {max}} &=& \left( 1-D\right) I_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] と求められ，\( \ I_{\mathrm {min}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {min}} &=& I_{\mathrm {max}}-I_{\mathrm {o}} \\[ 5pt ] &=& \left( 1-D\right) I_{\mathrm {o}}-I_{\mathrm {o}} \\[ 5pt ] &=& -DI_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)a.\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)の概略図
与えられている微分方程式
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) +RC\frac {\mathrm {d}v_{\mathrm {c}}^{\prime }\left( t \right) }{\mathrm {d}t} =-Ri_{\mathrm {s1}}^{\prime }\left( t \right) =
\begin{cases}
-RI_{\mathrm {max}} & \left( 0≦t＜DT \right) \\
-RI_{\mathrm {min}} & \left( DT≦t＜T \right) \\
\end{cases}
\end{eqnarray}
\] について，定常解は与えられているので，過渡解\( \ v_{\mathrm {ct}}^{\prime }\left( t \right) \ \)を求める。微分方程式の右辺を零とし，変数分離すると，
\[
\begin{eqnarray}
v_{\mathrm {ct}}^{\prime }\left( t \right) +RC\frac {\mathrm {d}v_{\mathrm {ct}}^{\prime }\left( t \right) }{\mathrm {d}t} &=&0 \\[ 5pt ] RC\frac {\mathrm {d}v_{\mathrm {ct}}^{\prime }\left( t \right) }{\mathrm {d}t} &=&-v_{\mathrm {ct}}^{\prime }\left( t \right) \\[ 5pt ] \frac {1}{v_{\mathrm {ct}}^{\prime }\left( t \right) }\mathrm {d}v_{\mathrm {ct}}^{\prime }\left( t \right) &=&-\frac {1}{RC}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，両辺積分すると，
\[
\begin{eqnarray}
\int \frac {1}{v_{\mathrm {ct}}^{\prime }\left( t \right) }\mathrm {d}v_{\mathrm {ct}}^{\prime }\left( t \right) &=&\int \left( -\frac {1}{RC}\right) \mathrm {d}t \\[ 5pt ] \ln v_{\mathrm {ct}}^{\prime }\left( t \right) &=&-\frac {1}{RC}t+C \\[ 5pt ] v_{\mathrm {ct}}^{\prime }\left( t \right) &=&A\mathrm {e}^{-\frac {1}{RC}t} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，一般解は，
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) &=&
\begin{cases}
-RI_{\mathrm {max}}+A_{1}\mathrm {e}^{-\frac {1}{RC}t} & \left( 0≦t＜DT \right) \\
-RI_{\mathrm {min}}+A_{2}\mathrm {e}^{-\frac {1}{RC}t} & \left( DT≦t＜T \right) \\
\end{cases} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ v_{\mathrm {c}}^{\prime }\left( 0 \right) \ \)が最大値，\( \ v_{\mathrm {c}}^{\prime }\left( DT \right) \ \)が最小値であるから，
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( 0 \right) &=&-RI_{\mathrm {max}}+A_{1} \\[ 5pt ] A_{1} &=&v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {max}} \\[ 5pt ] v_{\mathrm {c}}^{\prime }\left( DT \right) &=&-RI_{\mathrm {min}}+A_{2}\mathrm {e}^{-\frac {1}{RC}DT} \\[ 5pt ] A_{2} &=&\left\{ v_{\mathrm {c}}^{\prime }\left( DT \right) +RI_{\mathrm {min}} \right\} \mathrm {e}^{\frac {1}{RC}DT} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) &=&
\begin{cases}
-RI_{\mathrm {max}}+\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {max}}\right\}\mathrm {e}^{-\frac {1}{RC}t} & \left( 0≦t＜DT \right) \\
-RI_{\mathrm {min}}+\left\{ v_{\mathrm {c}}^{\prime }\left( DT \right) +RI_{\mathrm {min}} \right\}\mathrm {e}^{-\frac {1}{RC}\left( t-DT\right) } & \left( DT≦t＜T \right) \\
\end{cases} \\[ 5pt ] \end{eqnarray}
\] と求められる。さらに，(1)b.より，\( \ I_{\mathrm {max}}=\left( 1-D\right) I_{\mathrm {o}} \ \)，\( \ I_{\mathrm {min}}=-D I_{\mathrm {o}} \ \)であるから，
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) &=&
\begin{cases}
-RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\mathrm {e}^{-\frac {1}{RC}t} & \left( 0≦t＜DT \right) \\
RI_{\mathrm {o}}D+\left\{ v_{\mathrm {c}}^{\prime }\left( DT \right) -RI_{\mathrm {o}}D \right\}\mathrm {e}^{-\frac {1}{RC}\left( t-DT\right) } & \left( DT≦t＜T \right) \\
\end{cases} \\[ 5pt ] \end{eqnarray}
\] となり，上式より，グラフは指数関数的に変化するため，図3のように求められる。

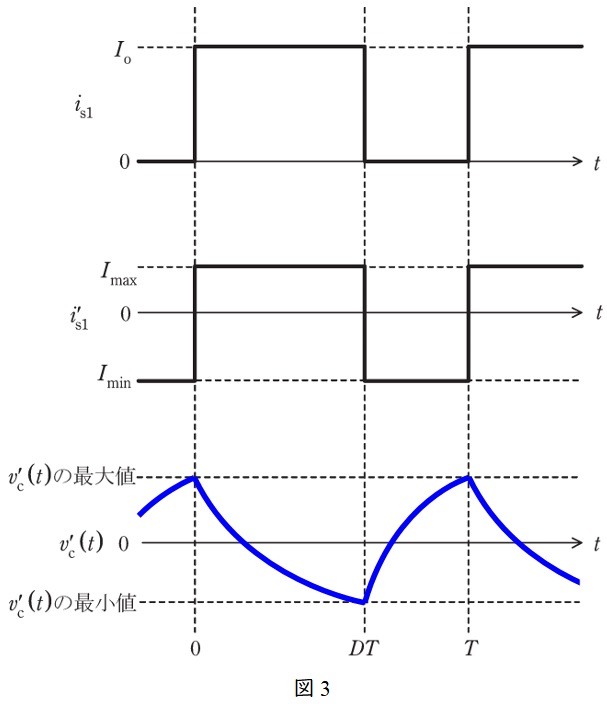
(2)b.交流成分\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)の波形が三角波で近似することができる条件
(2)a.の\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)の解より，\( \ RC \ \)が十分に大きい値ならば\( \ v_{\mathrm {c}}^{\prime }\left( t \right) \ \)はほぼ直線に近似できることになる。さらに通流率\( \ D \ \)を\( \ 0.5 \ \)とすればより三角波に近づくことになる。

(2)c.三角波として近似したときの\( \ \Delta v_{\mathrm {c}}^{\prime }=kI_{\mathrm {o}} \ \)の比例係数\( \ k \ \)
三角波として近似できると仮定すると，ワンポイント解説「5.マクローリン展開」の通り，
\[
\begin{eqnarray}
\mathrm {e}^{x} &≃&1 + x \\[ 5pt ] \end{eqnarray}
\] と近似できるので，
\[
\begin{eqnarray}
v_{\mathrm {c}}^{\prime }\left( t \right) &=&
\begin{cases}
\displaystyle -RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\left( 1-\frac {1}{RC}t\right) & \left( 0≦t＜DT \right) \\
\displaystyle RI_{\mathrm {o}}D+\left\{ v_{\mathrm {c}}^{\prime }\left( DT \right) -RI_{\mathrm {o}}D \right\}\left\{ 1-\frac {1}{RC}\left( t-DT\right) \right\} & \left( DT≦t＜T \right) \\
\end{cases} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，リプル幅\( \ \Delta v_{\mathrm {c}}^{\prime } \ \)は，
\[
\begin{eqnarray}
\Delta v_{\mathrm {c}}^{\prime } &=&v_{\mathrm {c}}^{\prime }\left( 0 \right) -v_{\mathrm {c}}^{\prime }\left( DT \right) \\[ 5pt ] &=&-RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\left( 1-\frac {1}{RC}\times 0\right) -\left[ -RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\left( 1-\frac {1}{RC}\times DT\right) \right] \\[ 5pt ] &=&-RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}-\left[ -RI_{\mathrm {o}}\left( 1-D\right) +\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\left( 1-\frac {1}{RC}\times DT\right) \right] \\[ 5pt ] &=&-\left\{ v_{\mathrm {c}}^{\prime }\left( 0 \right) +RI_{\mathrm {o}}\left( 1-D\right) \right\}\left( -\frac {DT}{RC} \right) \\[ 5pt ] &=& \frac {\left( 1-D\right)DT}{C}I_{\mathrm {o}} +\frac {DT}{RC}v_{\mathrm {c}}^{\prime }\left( 0 \right) \\[ 5pt ] \end{eqnarray}
\] と求められ，\( \ RC≫T \ \)であるので比例定数\( \ k \ \)は，\( \ \displaystyle k=\frac {\left( 1-D\right)DT}{C} \ \)と求められる。