《理論》〈電気回路〉[H20:問3]ラプラス変換を利用した過渡現象の解析に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，回路の過渡現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式又は図を解答群の中から選び，その記号をマークシートに記入しなさい。

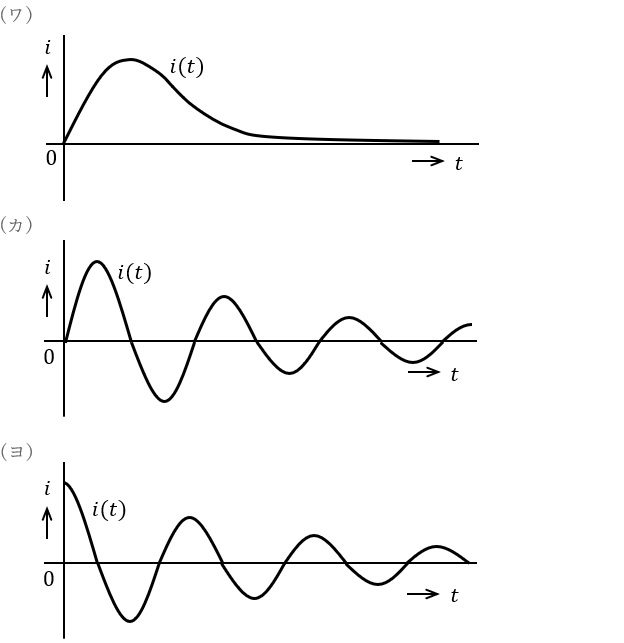
図の回路において，時刻に$ \ t=0 \ $でスイッチ$ \ \mathrm {SW} \ $を投入した後の電流$ \ i (t) \ $をラプラス変換を用いて求めたい。ただし，直流電圧源$ \ E=10 \ \mathrm {[V]} \ $，インダクタンス$ \ L=1 \ \mathrm {[H]} \ $，コンデンサ$ \ C=1 \ \mathrm {[F]} \ $，抵抗$ \ R=0.1 \ \mathrm {[\Omega ]} \ $とし，$ \ L \ $の初期電流を$ \ 0 \ \mathrm {[A]} \ $，$ \ C \ $の初期電荷を$ \ 0 \ \mathrm {[C]} \ $とする。また，$ \ \sin t \cdot u (t) \ $のラプラス変換は$ \ \displaystyle \frac {1}{s^{2}+1} \ $，$ \ \cos t \cdot u (t) \ $のラプラス変換は$ \ \displaystyle \frac {s}{s^{2}+1} \ $である（$ \ u(t) \ $は単位ステップ関数とする）。

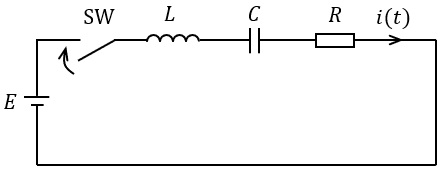
この回路の過渡現象を解析するための回路は$ \ t ＞ 0 \ $の状態の回路であるから，図においてスイッチを投入した状態の回路に対してキルヒホッフの電圧則と各素子の電圧・電流特性より，電流$ \ i (t) \ $に関する$ \ \fbox {　（１）　} \ $の方程式が得られる。電流$ \ i (t) \ $のラプラス変換を$ \ I (s) \ $で表すと式$ \ \fbox {　（１）　} \ $の両辺をラプラス変換して$ \ s \ $領域の方程式を求めることにより$ \ I (s)= \ \fbox {　（２）　} \ $が得られる。次に，$ \ I (s) \ $のラプラス逆変換を行い$ \ i (t) \ $を求めるため，式$ \ \fbox {　（２）　} \ $を$ \ I (s)≒ \ \fbox {　（３）　} \ $のように近似的に変形し，推移定理が使える形にする（ただし，$ \ 0.05^{2}≒0 \ $と近似する）。したがって，$ \ \fbox {　（３）　} \ $の$ \ I (s) \ $のラプラス逆変換により$ \ i (t) ≒ \ \fbox {　（４）　} \ \mathrm {[A]} \ $と求められる。このとき，$ \ i (t) \ $の時間波形は$ \ \fbox {　（５）　} \ $のようになる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {10}{s^{2}+0.1s+1}　　　　　&（ロ）&　\frac {\mathrm {d}^{2} i(t) }{\mathrm {d}t^{2}}+\int _{0}^{t}i( t^{\prime } )\mathrm {d}t^{\prime }+0.1\frac {\mathrm {d} i(t) }{\mathrm {d}t}=10u (t) \\[ 5pt ] &（ハ）&　\frac {\mathrm {d} i(t) }{\mathrm {d}t}+\int _{0}^{t}i( t^{\prime } )\mathrm {d}t^{\prime }+10 i(t)=10u (t)　　　　　&（ニ）&　\frac {10}{\left( s+0.05\right) ^{2}+1 }　 \\[ 5pt ] &（ホ）&　\frac {100}{\left( s+0.05\right) ^{2}+10^{2} }　　　　　&（ヘ）&　\frac {100}{s^{2}+0.1s+100} \\[ 5pt ] &（ト）&　\frac {10s}{\left( s+0.05\right) ^{2}+1 }　　　　　&（チ）&　10e^{0.05t}\sin t\cdot u(t) \\[ 5pt ] &（リ）&　\frac {\mathrm {d} i(t) }{\mathrm {d}t}+\int _{0}^{t}i( t^{\prime } )\mathrm {d}t^{\prime }+0.1 i(t)=10u (t)　　　　　&（ヌ）&　10e^{-0.05t}\cos t\cdot u(t) \\[ 5pt ] &（ル）&　10e^{-0.05t}\sin t\cdot u(t)　　　　　&（ヲ）&　\frac {10s}{s^{2}+0.1s+1} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ RLC \ $直列回路の過渡現象をラプラス変換を用いて求める問題です。
(3)の変形は少し迷うかもしれませんが，$ \ 2 \ $種二次試験で自動制御を学習された方であれば比較的容易に解けるかと思います。
完答できる受験生も多いと予想されますので，確実に理解しておくようにしましょう。

1.過渡現象における$ \ RLC \ $それぞれの電圧
過渡現象における$ \ RLC \ $それぞれの電圧は，線路に流れる電流を$ \ i \ $とし，抵抗$ \ R \ $の電圧$ \ v_{\mathrm{R}} \ $，リアクトル$ \ L \ $の電圧$ \ v_{\mathrm{L}} \ $，リアクトル$ \ C \ $の電圧$ \ v_{\mathrm{C}} \ $とすると，
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ] v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となります。

2.基本的なラプラス変換
$ \ f(t) \ $のラプラス変換を$ \ F(s) \ $とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ] {\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ] K & \displaystyle \frac {K}{s} \\[ 5pt ] t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ] \mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ] \sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ] 　　\cos \omega t　　 & 　　　\displaystyle \frac {s}{s^{2}+\omega ^{2}}　　　 \\[ 5pt ] \displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ] \displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ] \hline
\end{array}
\] 3.ラプラス変換の像の移動法則
任意の関数$ \ f (t)\mathrm {e}^{at} \ $のラプラス変換は$ \ F (s-a) \ $で表すことができ，これを像の移動法則といいます。代表的な関数を以下の表に示します。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
u (t) \mathrm {e}^{at} & \displaystyle \frac {1}{ s-a } \\[ 5pt ] t\mathrm {e}^{at} & \displaystyle \frac {1}{\left( s-a \right) ^{2}} \\[ 5pt ] \mathrm {e}^{at}\sin \omega t & \displaystyle \frac {\omega }{\left( s-a \right) ^{2}+\omega ^{2}} \\[ 5pt ] 　　\mathrm {e}^{at}\cos \omega t　　 & 　　\displaystyle \frac {s-a }{\left( s-a \right) ^{2}+\omega ^{2}}　　 \\[ 5pt ] \hline
\end{array}
\]

【解答】

(1)解答：リ
問題図について，回路方程式を立てると，ワンポイント解説「1.過渡現象における$ \ RLC \ $それぞれの電圧」の通り，
\[
\begin{eqnarray}
L\frac {\mathrm {d}i(t)}{\mathrm {d}t}+\frac {1}{C}\int i(t) \mathrm {d}t+Ri(t) &=& E \\[ 5pt ] \frac {\mathrm {d}i(t)}{\mathrm {d}t}+\int i(t) \mathrm {d}t+0.1i(t) &=& 10 \\[ 5pt ] \end{eqnarray}
\] となるので，解答群の形に書き換えれば，
\[
\begin{eqnarray}
\frac {\mathrm {d} i(t) }{\mathrm {d}t}+\int _{0}^{t}i( t^{\prime } )\mathrm {d}t^{\prime }+0.1 i(t)&=&10u (t) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：イ
$ \ L \ $の初期電流$ \ 0 \ \mathrm {[A]} \ $，$ \ C \ $の初期電荷$ \ 0 \ \mathrm {[C]} \ $に注意して，(1)解答式の両辺をラプラス変換すると，ワンポイント解説「2.基本的なラプラス変換」の通り，
\[
\begin{eqnarray}
sI(s) +\frac {I(s)}{s}+0.1I(s)&=&\frac {10}{s} \\[ 5pt ] \end{eqnarray}
\] となるので，これを$ \ I(s) \ $について整理すれば，
\[
\begin{eqnarray}
s^{2}I(s) +I(s)+0.1sI(s)&=&10 \\[ 5pt ] \left( s^{2} +0.1s+1\right) I(s)&=&10 \\[ 5pt ] I(s)&=&\frac {10}{s^{2}+0.1s+1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
(2)解答式を変形すると，
\[
\begin{eqnarray}
I(s)&=&\frac {10}{s^{2}+0.1s+1} \\[ 5pt ] &=&\frac {10}{\left( s+0.05 \right) ^{2}-0.05^{2}+1} \\[ 5pt ] &≒&\frac {10}{\left( s+0.05 \right) ^{2}+1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
(3)解答式を変形すると，
\[
\begin{eqnarray}
I(s)&=&\frac {10}{\left( s+0.05 \right) ^{2}+1} \\[ 5pt ] &=&10\cdot \frac {1}{\left( s+0.05 \right) ^{2}+1} \\[ 5pt ] \end{eqnarray}
\] となるので，これをラプラス逆変換すると，ワンポイント解説「3.ラプラス変換の像の移動法則」の通り，
\[
\begin{eqnarray}
i(t)&=&10e^{-0.05t}\sin t \\[ 5pt ] &=&10e^{-0.05t}\sin t\cdot u(t) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
(4)解答式は，正弦波と指数関数が組み合わされた関数なので，正弦波が減衰していく関数となる。したがって，解答は（カ）と求められる。