《理論》〈電気及び電子測定〉[H20:問4]Qメータを用いたコイルのインピーダンス測定に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，$ \ Q \ $メータを用いたコイルのインピーダンス測定に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式を解答群の中から選び，その記号をマークシートに記入しなさい。

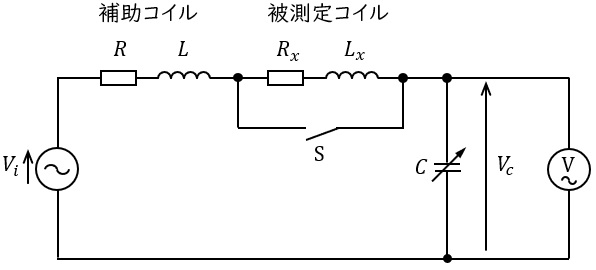
図は共振状態を利用してコイルのリアクタンス分と抵抗分を求める回路である。$ \ L \ $及び$ \ R \ $は補助コイルのインダクタンス分及び抵抗分，$ \ L_{x} \ $及び$ \ R_{x} \ $は被測定コイルのインダクタンス分及び抵抗分である。$ \ C \ $は損失が無視できる可変コンデンサの静電容量であり，その値を直読することができる。また，電圧$ \ V_{i} \ $，角周波数$ \ \omega \ $の交流電源が補助コイル，被測定コイル，可変コンデンサの直列回路に接続されている。ただし，Ⓥ（$ \ \mathrm {V} \ $に～のマーク）は理想的な電圧計で，$ \ C \ $の両端の電圧$ \ V_{c} \ $と入力電圧$ \ V_{i} \ $との比で目盛りが刻まれており，コイルの$ \ Q \ $の値$ \ \displaystyle \left( Q=\frac {V_{c}}{V_{i}}\right) \ $が直読できるものとする。

いま，スイッチ$ \ \mathrm {S} \ $を投入し，$ \ C \ $を調整して同調を取り共振状態が得られたときの$ \ C \ $の値を$ \ C_{1} \ $，$ \ Q \ $の値を$ \ Q_{1} \ $とすれば，
\[
\begin{eqnarray}
Q_{1} &=& \ \fbox {　（１）　} \ 　・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。次に，スイッチ$ \ \mathrm {S} \ $を開放し，$ \ C \ $を調整して同調を取り共振状態が得られたときの$ \ C \ $の値を$ \ C_{2} \ $，$ \ Q \ $の値を$ \ Q_{2} \ $とすれば，
\[
\begin{eqnarray}
Q_{2} &=& \ \fbox {　（２）　} \ 　・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。したがって，①式及び②式から$ \ R_{x} \ $は$ \ \fbox {　（３）　} \ $である。また，これら二つの共振条件から$ \ L_{x} \ $は$ \ \fbox {　（４）　} \ $と表される。

こうして求めた$ \ R_{x} \ $及び$ \ L_{x} \ $より，被測定コイルの$ \ Q \ $は$ \ \fbox {　（５）　} \ $で求められる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {C_{1}-C_{2}}{C_{1}Q_{1}-C_{2}Q_{2}}　　　　　&（ロ）&　\frac {\omega ^{2}C_{1}C_{2}}{C_{1}-C_{2}}　　　　　&（ハ）&　\frac {C_{1}-C_{2}}{C_{1}C_{2}} \\[ 5pt ] &（ニ）&　\frac {\omega C_{1}C_{2}Q_{1}Q_{2}}{C_{1}Q_{1}-C_{2}Q_{2}}　　　　　　　&（ホ）&　\frac {C_{1}Q_{1}-C_{2}Q_{2}}{C_{1}C_{2}}　　　　　&（ヘ）&　\frac {Q_{1}Q_{2}}{C_{1}Q_{1}-C_{2}Q_{2}} \\[ 5pt ] &（ト）&　\frac {1}{C_{1}}　　　　　&（チ）&　\frac {Q_{1}Q_{2}\left( C_{1}-C_{2}\right) }{C_{1}Q_{1}-C_{2}Q_{2}}　　　　　　　&（リ）&　\frac {C_{1}Q_{1}-C_{2}Q_{2}}{\omega C_{1}C_{2}Q_{1}Q_{2}} \\[ 5pt ] &（ヌ）&　\frac {1}{\omega C_{1}R}　　　　　&（ル）&　\frac {C_{1}-C_{2}}{\omega ^{2}C_{1}C_{2}}　　　　　&（ヲ）&　\omega C_{2}\left( R+R_{x}\right) \\[ 5pt ] &（ワ）&　\frac {1}{\omega C_{2}\left( R+R_{x}\right) }　　　　　&（カ）&　\frac {1}{\omega C_{2}R_{x}}　　　　　　&（ヨ）&　\frac {1}{\omega ^{2}C_{1}R} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

共振回路を用いたコイルのインピーダンス測定の問題です。
特別な公式や知識はそれほど必要としませんが，式変形に悩む問題です。
問題文の情報を整理しながら正答を導き出すようにして下さい。

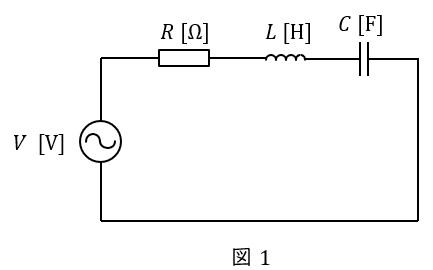
1.直列回路の共振回路
図1のような$ \ RLC \ $直列回路があった場合の合成インピーダンス$ \ \dot Z \ \mathrm {[\Omega ]} \ $は，角周波数を$ \ \omega \ \mathrm {[rad / s]} \ $とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数$ \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ $は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を$ \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ $とすると，$ \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ $より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

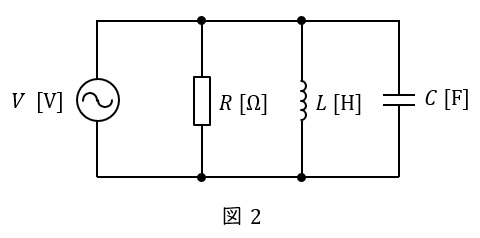
2.並列回路の共振回路
図2のような$ \ RLC \ $並列回路があった場合の合成アドミタンス$ \ \dot Y \ \mathrm {[S]} \ $は，角周波数を$ \ \omega \ \mathrm {[rad / s]} \ $とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数$ \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ $は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を$ \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ $とすると，$ \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ $より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヌ
ワンポイント解説「1.直列回路の共振回路」の通り，直列共振時の$ \ L \ $と$ \ C_{1} \ $の合成インピーダンスは零であるから，回路に流れる電流$ \ I \ $は，
\[
\begin{eqnarray}
I &=& \frac {V_{i}}{R} \\[ 5pt ] \end{eqnarray}
\] なので，$ \ C \ $の両端の電圧$ \ V_{c} \ $は，
\[
\begin{eqnarray}
V_{c} &=& \frac {1}{\omega C_{1}}I \\[ 5pt ] &=& \frac {V_{i}}{\omega C_{1}R} \\[ 5pt ] \end{eqnarray}
\] となる。よって，コイルの$ \ Q_{1} \ $は，
\[
\begin{eqnarray}
Q_{1} &=& \frac {V_{c}}{V_{i}} \\[ 5pt ] &=& \frac {\displaystyle \frac {V_{i}}{\omega C_{1}R}}{V_{i}} \\[ 5pt ] &=& \frac {1}{\omega C_{1}R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ワ
(1)と同様に回路に流れる電流$ \ I_{x} \ $は，
\[
\begin{eqnarray}
I_{x} &=& \frac {V_{i}}{R+R_{x}} \\[ 5pt ] \end{eqnarray}
\] なので，$ \ C \ $の両端の電圧$ \ V_{c} \ $は，
\[
\begin{eqnarray}
V_{c} &=& \frac {1}{\omega C_{2}}I \\[ 5pt ] &=& \frac {V_{i}}{\omega C_{2}\left( R+R_{x}\right) } \\[ 5pt ] \end{eqnarray}
\] となる。よって，コイルの$ \ Q_{2} \ $は，
\[
\begin{eqnarray}
Q_{2} &=& \frac {V_{c}}{V_{i}} \\[ 5pt ] &=& \frac {\displaystyle \frac {V_{i}}{\omega C_{2}\left( R+R_{x}\right) }}{V_{i}} \\[ 5pt ] &=& \frac {1}{\omega C_{2}\left( R+R_{x}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
(1)解答式より，
\[
\begin{eqnarray}
R &=& \frac {1}{\omega C_{1}Q_{1}} \\[ 5pt ] \end{eqnarray}
\] であるから，これを(2)解答式に代入して整理すると，
\[
\begin{eqnarray}
Q_{2} &=& \frac {1}{\omega C_{2}\left( \displaystyle \frac {1}{\omega C_{1}Q_{1}}+R_{x}\right) } \\[ 5pt ] &=& \frac {1}{\displaystyle \frac {C_{2}}{C_{1}Q_{1}}+\omega C_{2}R_{x} } \\[ 5pt ] \frac {C_{2}}{C_{1}Q_{1}}+\omega C_{2}R_{x} &=& \frac {1}{Q_{2}} \\[ 5pt ] \omega C_{2}R_{x} &=& \frac {1}{Q_{2}}-\frac {C_{2}}{C_{1}Q_{1}} \\[ 5pt ] R_{x} &=& \frac {1}{\omega C_{2}Q_{2}}-\frac {1}{\omega C_{1}Q_{1}} \\[ 5pt ] &=& \frac {C_{1}Q_{1}-C_{2}Q_{2}}{\omega C_{1}C_{2}Q_{1}Q_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
スイッチ$ \ \mathrm {S} \ $投入時の共振条件より，
\[
\begin{eqnarray}
\omega L &=& \frac {1}{\omega C_{1}} \\[ 5pt ] L &=& \frac {1}{\omega ^{2}C_{1}} \\[ 5pt ] \end{eqnarray}
\] であり，これとスイッチ$ \ \mathrm {S} \ $開放時の共振条件より，
\[
\begin{eqnarray}
\omega \left( L+L_{x}\right) &=& \frac {1}{\omega C_{2}} \\[ 5pt ] L+L_{x} &=& \frac {1}{\omega ^{2} C_{2}} \\[ 5pt ] \frac {1}{\omega ^{2}C_{1}}+L_{x} &=& \frac {1}{\omega ^{2} C_{2}} \\[ 5pt ] L_{x} &=& \frac {1}{\omega ^{2} C_{2}}-\frac {1}{\omega ^{2}C_{1}} \\[ 5pt ] &=& \frac {C_{1}-C_{2}}{\omega ^{2} C_{1}C_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
(1)解答式より，共振時の$ \ C \ $の値を$ \ C_{3} \ $，$ \ Q \ $の値を$ \ Q_{3} \ $とすれば，
\[
\begin{eqnarray}
Q_{3} &=& \frac {1}{\omega C_{3}R_{x}} \\[ 5pt ] \end{eqnarray}
\] であり，直列共振の条件から$ \ \displaystyle \omega L_{x}=\frac {1}{\omega C_{3}} \ $であるので，
\[
\begin{eqnarray}
Q_{3} &=& \frac {\omega L_{x}}{R_{x}} \\[ 5pt ] &=& \frac {\displaystyle \omega \frac {C_{1}-C_{2}}{\omega ^{2} C_{1}C_{2}}}{\displaystyle \frac {C_{1}Q_{1}-C_{2}Q_{2}}{\omega C_{1}C_{2}Q_{1}Q_{2}}} \\[ 5pt ] &=& \frac {\displaystyle C_{1}-C_{2}}{\displaystyle \frac {C_{1}Q_{1}-C_{2}Q_{2}}{ Q_{1}Q_{2}}} \\[ 5pt ] &=& \frac {Q_{1}Q_{2}\left( C_{1}-C_{2}\right) }{C_{1}Q_{1}-C_{2}Q_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。