【問題】
【難易度】★★★☆☆(普通)
次の文章は,分布定数回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
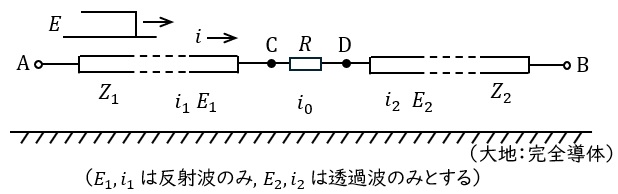
図のように,特性インピーダンスが\( \ Z_{1} \ \)と\( \ Z_{2} \ \)の\( \ 2 \ \)本の非常に長い無損失線路が接続点\( \ \mathrm {C} \ \),\( \ \mathrm {D} \ \)で抵抗\( \ R \ \)を介して接続されている。端子\( \ \mathrm {A} \ \)から接続点\( \ \mathrm {C} \ \)に向かって波頭が階段状で波高値\( \ E \ \)の電圧波が進入した。このときの接続点\( \ \mathrm {C} \ \)での反射波の波高値と端子\( \ \mathrm {B} \ \)側への透過波の波高値を測定した。抵抗\( \ R \ \)の値が既知であるとき,\( \ Z_{1} \ \),\( \ Z_{2} \ \)を求めたい。ただし,両線路間に電気的・磁気的結合はなく,また\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)それぞれの端子では反射はないものとする。抵抗\( \ R \ \)は集中定数素子である。
入射波による電流\( \ i \ \),接続点\( \ \mathrm {C} \ \)での反射波により生じる電圧\( \ E_{1} \ \),電流\( \ i_{1} \ \),抵抗\( \ R \ \)に流れる電流\( \ i_{0} \ \),端子\( \ \mathrm {B} \ \)側への透過波による電圧\( \ E_{2} \ \),電流\( \ i_{2} \ \)を図のようにとる。電流は端子\( \ \mathrm {A} \ \)側から端子\( \ \mathrm {B} \ \)側に向かって進行する方向を正とする。
接続点\( \ \mathrm {C} \ \)での電圧,電流の関係はそれぞれ次式で表される。
\[
\begin{eqnarray}
\left.
\begin{array}{l}
&&E + E_{1} = \ \fbox { (1) } \ \\
&&i + i_{1} = i_{0}
\end{array}
\right\} ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
また,
\[
\begin{eqnarray}
\left.
\begin{array}{l}
\ &&E = Z_{1}i \\
&&E_{1} = -Z_{1}i_{1} \\
&&E_{2} = Z_{2}i_{2} \\
\end{array}
\right\} ・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
である。これらの式と\( \ i_{0} = i_{2} \ \)を考慮して,接続点\( \ \mathrm {C} \ \)での反射波の波高値\( \ E_{1} \ \)と端子\( \ \mathrm {B} \ \)側への透過波の波高値\( \ E_{2} \ \)を\( \ E \ \),\( \ Z_{1} \ \),\( \ Z_{2} \ \),\( \ R \ \)を用いて表すと,
\[
\begin{eqnarray}
\left.
\begin{array}{l}
&& E_{1} = \ \fbox { (2) } \ \\
&&E_{2} = \ \fbox { (3) }
\end{array}
\ \right\} ・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となる。
\( \ E_{1} \ \)と\( \ E_{2} \ \)の測定値がそれぞれ\( \ \displaystyle E_{1}=\frac {E}{2} \ \),\( \ \displaystyle E_{2}=\frac {E}{8} \ \)であった。これらの値と③式より\( \ Z_{1} \ \),\( \ Z_{2} \ \)と\( \ R \ \)の関係を求めると,
\[
\begin{eqnarray}
Z_{1} &=& \ \fbox { (4) } \ \\[ 5pt ]
Z_{2} &=& \ \fbox { (5) } \ \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R-Z_{1}-Z_{2}}{R+Z_{1}-Z_{2}}E &(ロ)& \frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}}E &(ハ)& \frac {2Z_{2}}{R+Z_{1}-Z_{2}}E \\[ 5pt ]
&(ニ)& Ri_{0}+E_{2} &(ホ)& \frac {2Z_{2}}{R+Z_{1}+Z_{2}}E &(ヘ)& \frac {4}{11}R \\[ 5pt ]
&(ト)& \frac {1}{10}R &(チ)& Ri_{0} &(リ)& \frac {2Z_{2}}{R+Z_{1}}E \\[ 5pt ]
&(ヌ)& \frac {1}{12}R &(ル)& \frac {2}{5}R &(ヲ)& \frac {1}{3}R \\[ 5pt ]
&(ワ)& \frac {R-Z_{1}}{R+Z_{1}}E &(カ)& \frac {1}{11}R &(ヨ)& Ri_{0}-E_{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
分布定数回路における特性インピーダンス\( \ Z_{1} \ \),\( \ Z_{2} \ \)を求める問題です。
通常二次試験の電力管理科目で出題される内容ですが,この年は理論科目で出題されました。一次試験の段階から二次試験の勉強を進めている受験生も多いと思いますので,そういう方であれば問題なく解けたかと思います。
ある程度立式のパターンは決まっていますので,関係式を立てられるように準備しておいて下さい。
1.分布定数回路における接続点での関係式
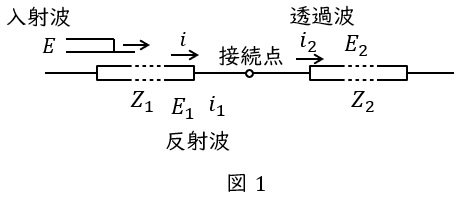
図1のような,特性インピーダンスが\( \ Z_{1} \ \)及び\( \ Z_{2} \ \)の非常に長い無損失線路が接続されているときの接続点での関係式を考えます。
図の左側から波高値\( \ E \ \)の電圧波が進入すると,接続点で一部の電圧が反射し,残りの電圧が透過します。このとき,入射波による電流を\( \ i \ \),反射波により生じる電圧及び電流を\( \ E_{1} \ \)及び\( \ i_{1} \ \),透過波により生じる電圧及び電流を\( \ E_{2} \ \)及び\( \ i_{2} \ \)とし,いずれの電流も右向きに流れる電流を正とすると,以下の電圧と電流の関係式が成り立ちます。
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ]
i +i_{1}&=&i_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,各電圧と電流には,
\[
\begin{eqnarray}
E&=&Z_{1}i \\[ 5pt ]
E_{1}&=&-Z_{1}i_{1} \\[ 5pt ]
E_{2}&=&Z_{2}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
※ 右向きを正とするので,電流\( \ i_{1} \ \)が負の値になることに注意しましょう。
【解答】
(1)解答:ニ
ワンポイント解説「1.分布定数回路における接続点での関係式」の通り,接続点で反射波と透過波に分かれ,さらに透過波において\( \ R \ \)での電圧降下が発生するので,
\[
\begin{eqnarray}
E +E_{1}&=&Ri_{0}+E_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ロ
\( \ i_{0} = i_{2} \ \)を考慮し,②式を変形すると,
\[
\begin{eqnarray}
\left.
\begin{array}{l}
&&i =\displaystyle \frac {E}{Z_{1}} \\
&&i_{1} = \displaystyle -\frac {E_{1}}{Z_{1}} \\
&&i_{2}=i_{0}=\displaystyle \frac {E_{2}}{Z_{2}} \\
\end{array}
\right\} ・・・・・・・・・・ ②^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを①式の\( \ i + i_{1} = i_{0} \ \)に代入すると,
\[
\begin{eqnarray}
\frac {E}{Z_{1}} -\frac {E_{1}}{Z_{1}} &=&\frac {E_{2}}{Z_{2}} \\[ 5pt ]
\frac {Z_{2}}{Z_{1}}\left( E -E_{1}\right) &=&E_{2} \ ・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となる。次に,(1)解答式に\( \ ②^{\prime } \ \)式を代入し整理すると,
\[
\begin{eqnarray}
E +E_{1}&=&Ri_{0}+E_{2} \\[ 5pt ]
&=&\frac {RE_{2}}{Z_{2}}+E_{2} \\[ 5pt ]
&=&\frac {R+Z_{2}}{Z_{2}}E_{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに④式を代入すると,
\[
\begin{eqnarray}
E +E_{1}&=&\frac {R+Z_{2}}{Z_{2}}\cdot \frac {Z_{2}}{Z_{1}}\left( E -E_{1}\right) \\[ 5pt ]
&=&\frac {R+Z_{2}}{Z_{1}}\left( E -E_{1}\right) \\[ 5pt ]
Z_{1}E +Z_{1}E_{1}&=&\left( R+Z_{2}\right) E-\left( R+Z_{2}\right) E_{1} \\[ 5pt ]
Z_{1}E_{1}+\left( R+Z_{2}\right) E_{1}&=&\left( R+Z_{2}\right) E-Z_{1}E \\[ 5pt ]
\left( R+Z_{1}+Z_{2}\right) E_{1}&=&\left( R-Z_{1}+Z_{2}\right) E \\[ 5pt ]
E_{1}&=&\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
(2)解答式を④に代入すると,
\[
\begin{eqnarray}
E_{2}&=&\frac {Z_{2}}{Z_{1}}\left( E -E_{1}\right) \\[ 5pt ]
&=&\frac {Z_{2}}{Z_{1}}\left( E -\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} E \right) \\[ 5pt ]
&=&\frac {Z_{2}}{Z_{1}}\left( \frac {R+Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} -\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} \right) E \\[ 5pt ]
&=&\frac {Z_{2}}{Z_{1}} \frac {2Z_{1}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
&=&\frac {2Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
(2)解答式に\( \ \displaystyle E_{1}=\frac {E}{2} \ \)を代入して整理すると,
\[
\begin{eqnarray}
E_{1}&=&\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\frac {E}{2}&=&\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\frac {1}{2}&=&\frac {R-Z_{1}+Z_{2}}{R+Z_{1}+Z_{2}} \\[ 5pt ]
R+Z_{1}+Z_{2}&=&2R-2Z_{1}+2Z_{2} \\[ 5pt ]
3Z_{1}-Z_{2}&=&R ・・・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に(3)解答式に\( \ \displaystyle E_{2}=\frac {E}{8} \ \)を代入して整理すると,
\[
\begin{eqnarray}
E_{2}&=&\frac {2Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\frac {E}{8}&=&\frac {2Z_{2}}{R+Z_{1}+Z_{2}} E \\[ 5pt ]
\frac {1}{8}&=&\frac {2Z_{2}}{R+Z_{1}+Z_{2}} \\[ 5pt ]
R+Z_{1}+Z_{2}&=&16Z_{2} \\[ 5pt ]
Z_{1}-15Z_{2}&=&-R ・・・・・・・・・・・・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ ⑤\times 15-⑥ \ \)より,
\[
\begin{eqnarray}
44Z_{1}&=&16R \\[ 5pt ]
Z_{1}&=&\frac {4}{11}R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(4)解答式を⑤式に代入すれば,
\[
\begin{eqnarray}
3Z_{1}-Z_{2}&=&R \\[ 5pt ]
3\cdot \frac {4}{11}R-Z_{2}&=&R \\[ 5pt ]
\frac {12}{11}R-Z_{2}&=&R \\[ 5pt ]
Z_{2}&=&\frac {12}{11}R-R \\[ 5pt ]
&=&\frac {1}{11}R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん