《理論》〈電磁気〉[H22:問6]誘電体挿入時の平行平板コンデンサの特性に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，平行平板電極と誘電体に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式を解答群の中から選びなさい。

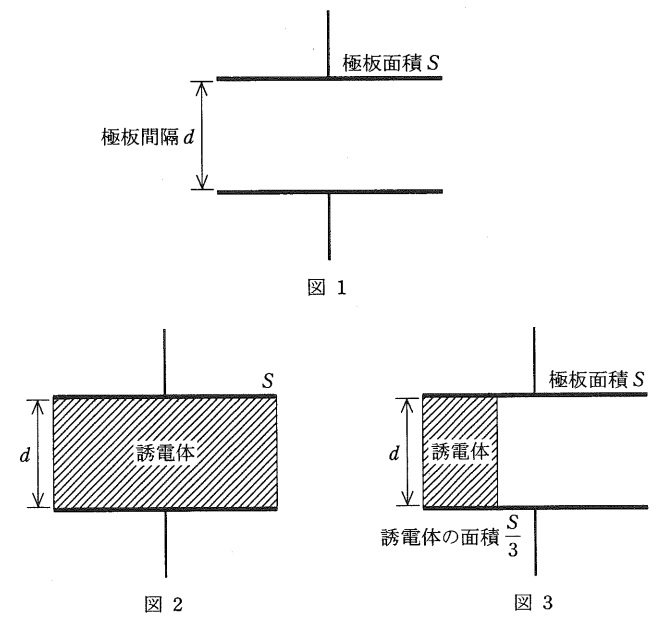
図1のように，真空中に極板面積が$ \ S \ $，極板間隔が$ \ d \ $の平行平板電極があり，$ \ S \ $は$ \ d \ $に比べて十分大きいとする。この電極間の電圧が$ \ V \ $になるまで充電し，電源から切り離した。これを初期状態とする。真空の誘電率を$ \ \varepsilon _{0} \ $ とするとき，以下の関係が成り立つ。ただし，端部の影響は無視できるものとする。

a.初期状態で一方の極板に蓄えられる電荷量は$ \ \fbox {　（１）　} \ $であり，電極間に働く力の大きさは$ \ \fbox {　（２）　} \ $である。

b.初期状態にある平行平板電極間に，図2のように厚さが$ \ d \ $，比誘電率が$ \ \varepsilon _{\mathrm {r}} \ $の誘電体を，極板と接する面積が$ \ S \ $になるように挿入した。このときの電極間の電圧は$ \ \fbox {　（３）　} \ $となる。

c.初期状態にある平行平板電極間に，図3のように厚さが$ \ d \ $，比誘電率が$ \ \varepsilon _{\mathrm {r}} \ $の誘電体を，極板と接する面積が$ \ \displaystyle \frac {S}{3} \ $になるように挿入した。このとき，電極間の電圧は$ \ \fbox {　（４）　} \ $となり，全体の静電容量は$ \ \fbox {　（５）　} \ $となる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {3}{2-\varepsilon _{\mathrm {r}}}V　　　　　&（ロ）&　\frac {V}{\varepsilon _{\mathrm {r}}^{2}}　　　　　&（ハ）&　\frac {3}{2+\varepsilon _{\mathrm {r}}}V \\[ 5pt ] &（ニ）&　\frac {2\varepsilon _{\mathrm {r}}}{3}\cdot \frac {\varepsilon _{\mathrm {0}}S}{d}　　　　　&（ホ）&　\frac {\varepsilon _{\mathrm {0}}SV^{2}}{2d^{2}}　　　　　&（ヘ）&　\frac {2+\varepsilon _{\mathrm {r}}}{3}\cdot \frac {\varepsilon _{\mathrm {0}}S}{d} \\[ 5pt ] &（ト）&　\frac {\varepsilon _{\mathrm {0}}SV^{2}}{2d}　　　　　&（チ）&　\frac {\varepsilon _{\mathrm {0}}SV^{2}}{d^{2}}　　　　　&（リ）&　\frac {\varepsilon _{\mathrm {0}}V}{d} \\[ 5pt ] &（ヌ）&　\frac {\varepsilon _{\mathrm {0}}SV}{d}　　　　　&（ル）&　\frac {\varepsilon _{\mathrm {0}}S}{d}　　　　　&（ヲ）&　\varepsilon _{\mathrm {r}}V \\[ 5pt ] &（ワ）&　\frac {V}{\varepsilon _{\mathrm {r}}}　　　　　&（カ）&　\frac {3}{2\varepsilon _{\mathrm {r}}}V　　　　　&（ヨ）&　\frac {2-\varepsilon _{\mathrm {r}}}{3}\cdot \frac {\varepsilon _{\mathrm {0}}S}{d} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

充電した平行平板コンデンサに誘電体を挿入した際の各諸量を求める問題です。
(2)以外は$ \ 2 \ $種や$ \ 3 \ $種で学習してきた内容ですから，積極的に選択したい問題と言えるかと思います。

1.電荷$ \ Q \ $と静電容量$ \ C \ $及び電圧$ \ V \ $の関係
平行平板コンデンサにおいて，蓄えられる電荷$ \ Q \ \mathrm {[C]} \ $と静電容量$ \ C \ \mathrm {[F]} \ $及び電圧$ \ V \ \mathrm {[V]} \ $には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量$ \ C \ $
平行平板コンデンサの静電容量$ \ C \ \mathrm {[F]} \ $は，真空の誘電率を$ \ \varepsilon _{0} \ \mathrm {[F / m]} \ $，極板の面積を$ \ S \ \mathrm {[m^{2}]} \ $，極板間の距離を$ \ d \ \mathrm {[m]} \ $とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。平行平板コンデンサの間に比誘電率$ \ \varepsilon _{\mathrm {r}} \ $の誘電体を挿入すると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.平行平板コンデンサの電界$ \ E \ $と電圧$ \ V \ $の関係
極板間の距離$ \ d \ \mathrm {[m]} \ $の平行平板コンデンサに電圧$ \ V \ \mathrm {[V]} \ $をかけると，極板間の電界$ \ E \ \mathrm {[V / m]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

4.平行平板コンデンサの静電エネルギー$ \ W \ $
静電容量$ \ C \ \mathrm {[F]} \ $の平行平板コンデンサに電圧$ \ V \ \mathrm {[V]} \ $をかけたときに蓄えられる静電エネルギー$ \ W \ \mathrm {[J]} \ $は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，$ \ Q=CV \ $の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヌ
初期状態での静電容量$ \ C_{0} \ $は，ワンポイント解説「2.平行平板コンデンサの静電容量$ \ C \ $」の通り，
\[
\begin{eqnarray}
C_{0} &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] であるから，蓄えられる電荷量$ \ Q \ $は，ワンポイント解説「1.電荷$ \ Q \ $と静電容量$ \ C \ $及び電圧$ \ V \ $の関係」の通り，
\[
\begin{eqnarray}
Q &=&C_{0}V \\[ 5pt ] &=&\frac {\varepsilon _{\mathrm {0}}SV}{d} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
平行平板コンデンサに蓄えられる静電エネルギー$ \ W \ $は，ワンポイント解説「4.平行平板コンデンサの静電エネルギー$ \ W \ $」の通り，
\[
\begin{eqnarray}
W &=&\frac {1}{2}C_{0}V^{2} \\[ 5pt ] &=&\frac {\varepsilon _{0}SV^{2}}{2d} \\[ 5pt ] \end{eqnarray}
\] であり，これが極板間に働く力の大きさ$ \ F \ $で極板間隔$ \ d \ $動かすのに必要なエネルギーに相当するから，
\[
\begin{eqnarray}
F &=&\frac {W}{d} \\[ 5pt ] &=&\frac {\displaystyle \frac {\varepsilon _{0}SV^{2}}{2d}}{d} \\[ 5pt ] &=&\frac {\varepsilon _{\mathrm {0}}SV^{2}}{2d^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
誘電体挿入後の静電容量$ \ C_{1} \ $は，ワンポイント解説「2.平行平板コンデンサの静電容量$ \ C \ $」の通り，
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] であり，誘電体挿入前後で蓄えられている電荷量$ \ \displaystyle Q=\frac {\varepsilon _{\mathrm {0}}SV}{d} \ $は変わらないから，このときの電極間の電圧$ \ V^{\prime } \ $は，
\[
\begin{eqnarray}
V^{\prime } &=&\frac {Q}{C_{1}} \\[ 5pt ] &=&\frac {\displaystyle \frac {\varepsilon _{\mathrm {0}}SV}{d}}{\displaystyle \frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d}} \\[ 5pt ] &=&\frac {V}{\varepsilon _{\mathrm {r}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
誘電体を極板と接する面積が$ \ \displaystyle \frac {S}{3} \ $になるようにしたときの静電容量$ \ C_{2} \ $は，２つのコンデンサの並列回路と考えられるから，
\[
\begin{eqnarray}
C_{2} &=&\frac {\displaystyle \varepsilon _{\mathrm {r}} \varepsilon _{0}\frac {S}{3}}{d} +\frac {\displaystyle \varepsilon _{0}\frac {2S}{3}}{d} \\[ 5pt ] &=&\frac {\varepsilon _{0}S}{3d}\left( \varepsilon _{\mathrm {r}}+2\right) \\[ 5pt ] \end{eqnarray}
\] となるので，極板間の電圧$ \ V^{\prime \prime } \ $は，電荷量$ \ \displaystyle Q=\frac {\varepsilon _{\mathrm {0}}SV}{d} \ $は変わらないので，
\[
\begin{eqnarray}
V^{\prime \prime } &=&\frac {Q}{C_{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {\varepsilon _{\mathrm {0}}SV}{d}}{\displaystyle \frac {\varepsilon _{0}S}{3d}\left( \varepsilon _{\mathrm {r}}+2\right) } \\[ 5pt ] &=&\frac {3}{2+\varepsilon _{\mathrm {r}}}V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヘ
(4)の$ \ C_{2} \ $を，解答群の式の形に合わせると，
\[
\begin{eqnarray}
C_{2} &=&\frac {\varepsilon _{0}S}{3d}\left( \varepsilon _{\mathrm {r}}+2\right) \\[ 5pt ] &=&\frac {2+\varepsilon _{\mathrm {r}}}{3}\cdot \frac {\varepsilon _{\mathrm {0}}S}{d} \\[ 5pt ] \end{eqnarray}
\] と求められる。