《理論》〈電子回路〉[H23:問7] バイポーラトランジスタに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

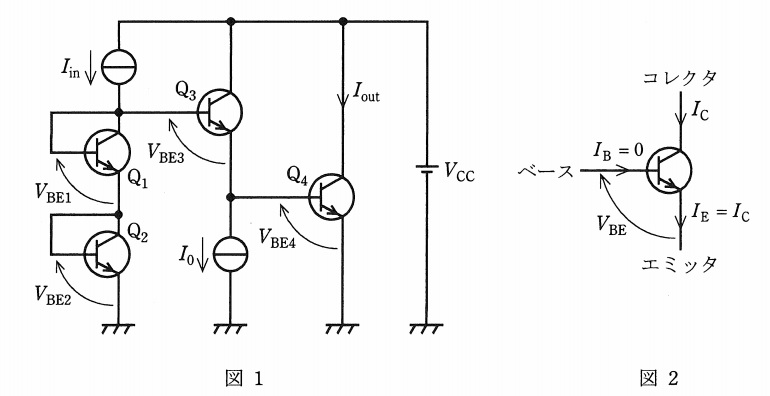
次の文章は，同一特性を有する$ \ 4 \ $個のバイポーラトランジスタを用いた直流で動作する図1の回路について，入力電流$ \ I_{\mathrm {in}} \ $と出力電流$ \ I_{\mathrm {out}} \ $の関係を求める過程に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。ただし，直流電圧源$ \ V_{\mathrm {CC}} \ $の値は十分大きいものとする。また，バイポーラトランジスタのコレクタ電流$ \ I_{\mathrm {C}} \ $，ベース電流$ \ I_{\mathrm {B}} \ $，エミッタ電流$ \ I_{\mathrm {E}} \ $，ベース・エミッタ間電圧$ \ V_{\mathrm {BE}} \ $は図2のとおりに定義され，$ \ I_{\mathrm {B}} \ $は零，$ \ I_{\mathrm {E}} \ $は$ \ I_{\mathrm {C}} \ $に等しく，$ \ I_{\mathrm {C}} \ $は熱電圧$ \ V_{\mathrm {T}} \ $，逆方向飽和電流$ \ I_{\mathrm {S}} \ $によって，
\[
I_{\mathrm {C}}=I_{\mathrm {S}}\mathrm {e}^{\frac {V_{\mathrm {BE}}}{V_{\mathrm {T}}}}　　　・・・・・・・・・・・①
\] と表されるものとする。
図1の回路において，$ \ i \ $番目($ \ i=1～4 \ $)のバイポーラトランジスタ$ \ \mathrm {Q}_{i} \ $のベース・エミッタ間電圧を$ \ V_{\mathrm {BE}i} \ $，コレクタ電流を$ \ I_{\mathrm {C}i} \ $とすると，四つのベース・エミッタ間電圧$ \ V_{\mathrm {BE1}}～V_{\mathrm {BE4}} \ $の間には
\[
\fbox {　（１）　}　　　　　　・・・・・・・・・・②
\] という関係が成り立つ。①式から$ \ V_{\mathrm {BE}i} \ $を$ \ I_{\mathrm {C}i} \ $と$ \ V_{\mathrm {T}} \ $，$ \ I_{\mathrm {S}} \ $で表すと
\[
\fbox {　（２）　}　　　　　　・・・・・・・・・・③
\] となる。この式を②式に代入すると，四つのコレクタ電流$ \ I_{\mathrm {C1}}～I_{\mathrm {C4}} \ $の間の関係として
\[
\fbox {　（３）　}　　　　　　・・・・・・・・・・④
\] が得られる。$ \ \mathrm {Q}_{1} \ $と$ \ \mathrm {Q}_{2} \ $のコレクタ電流が$ \ I_{\mathrm {in}} \ $，$ \ \mathrm {Q}_{3} \ $のコレクタ電流が$ \ \fbox {　（４）　} \ $，$ \ \mathrm {Q}_{4} \ $のコレクタ電流が$ \ I_{\mathrm {out}} \ $であることから，$ \ I_{\mathrm {out}} \ $は
\[
\fbox {　（５）　}　　　　　　・・・・・・・・・・⑤
\] となる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　I_{\mathrm {in}}　　　&（ロ）&　I_{\mathrm {C1}}I_{\mathrm {C2}}=I_{\mathrm {C3}}I_{\mathrm {C4}} \\[ 5pt ] &（ハ）&　V_{\mathrm {BE}i}=V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {S}}}{I_{\mathrm {C}i}}\right)　　　&（ニ）&　I_{\mathrm {out}}=\sqrt {I_{\mathrm {in}}I_{0}} \\[ 5pt ] &（ホ）&　V_{\mathrm {BE}i}=V_{\mathrm {T}}\frac {I_{\mathrm {S}}}{I_{\mathrm {C}i}}　　　&（ヘ）&　I_{0} \\[ 5pt ] &（ト）&　I_{\mathrm {out}}=I_{\mathrm {in}}　　　&（チ）&　V_{\mathrm {BE1}}+V_{\mathrm {BE2}}=V_{\mathrm {BE3}}+V_{\mathrm {BE4}} \\[ 5pt ] &（リ）&　\frac {I_{\mathrm {C1}}}{I_{\mathrm {C2}}}=\frac {I_{\mathrm {C3}}}{I_{\mathrm {C4}}}　　　&（ヌ）&　I_{\mathrm {out}}=\frac {I^{2}_{\mathrm {in}}}{I_{0}} \\[ 5pt ] &（ル）&　I_{\mathrm {out}}　　　&（ヲ）&　I_{\mathrm {C1}}I_{\mathrm {C3}}=I_{\mathrm {C2}}I_{\mathrm {C4}} \\[ 5pt ] &（ワ）&　V_{\mathrm {BE1}}-V_{\mathrm {BE2}}=V_{\mathrm {BE3}}-V_{\mathrm {BE4}}　　　&（カ）&　V_{\mathrm {BE}i}=V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C}i}}{I_{\mathrm {S}}}\right) \\[ 5pt ] &（ヨ）&　V_{\mathrm {BE1}}+V_{\mathrm {BE3}}=V_{\mathrm {BE2}}+V_{\mathrm {BE4}}
\end{eqnarray}
\]

【ワンポイント解説】

バイポーラトランジスタの理解度を確認する問題です。バイポーラトランジスタの性質を理解し、問題に慣れてしまえば，確実に得点できる問題となります。

【解答】

(1)解答：チ
図1-1に示す電位を$ \ V_{\mathrm {in}} \ $とすると，図1-1に示す$ \ 2 \ $個の回路から，
\[
\begin{eqnarray}
V_{\mathrm {in}}&=&V_{\mathrm {BE1}}+V_{\mathrm {BE2}}=V_{\mathrm {BE3}}+V_{\mathrm {BE4}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：カ
①式を変形すると，
\[
\begin{eqnarray}
I_{\mathrm {C}i}&=&I_{\mathrm {S}}\mathrm {e}^{\frac {V_{\mathrm {BE}i}}{V_{\mathrm {T}}}} \\[ 5pt ] \frac {I_{\mathrm {C}i}}{I_{\mathrm {S}}}&=&\mathrm {e}^{\frac {V_{\mathrm {BE}i}}{V_{\mathrm {T}}}} \\[ 5pt ] \end{eqnarray}
\] となるので，両辺対数をとってさらに変形すると，
\[
\begin{eqnarray}
\ln \left (\frac {I_{\mathrm {C}i}}{I_{\mathrm {S}}}\right) &=&\frac {V_{\mathrm {BE}i}}{V_{\mathrm {T}}} \\[ 5pt ] V_{\mathrm {BE}i}&=&V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C}i}}{I_{\mathrm {S}}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
(2)解答式を(1)解答式の両辺に代入し整理すると，
\[
\begin{eqnarray}
V_{\mathrm {BE1}}+V_{\mathrm {BE2}}&=&V_{\mathrm {BE3}}+V_{\mathrm {BE4}} \\[ 5pt ] V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C1}}}{I_{\mathrm {S}}}\right)+V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C2}}}{I_{\mathrm {S}}}\right)&=&V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C3}}}{I_{\mathrm {S}}}\right)+V_{\mathrm {T}}\ln \left( \frac {I_{\mathrm {C4}}}{I_{\mathrm {S}}}\right) \\[ 5pt ] \ln \left( \frac {I_{\mathrm {C1}}}{I_{\mathrm {S}}}\right)+\ln \left( \frac {I_{\mathrm {C2}}}{I_{\mathrm {S}}}\right)&=&\ln \left( \frac {I_{\mathrm {C3}}}{I_{\mathrm {S}}}\right)+\ln \left( \frac {I_{\mathrm {C4}}}{I_{\mathrm {S}}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ \displaystyle \ln \left( \frac {A}{B} \right) =\ln A-\ln B \ $となるから，
\[
\begin{eqnarray}
\ln I_{\mathrm {C1}}-\ln I_{\mathrm {S}}+\ln I_{\mathrm {C2}}-\ln I_{\mathrm {S}}&=&\ln I_{\mathrm {C3}}-\ln I_{\mathrm {S}}+\ln I_{\mathrm {C4}}-\ln I_{\mathrm {S}} \\[ 5pt ] \ln I_{\mathrm {C1}}+\ln I_{\mathrm {C2}}&=&\ln I_{\mathrm {C3}}+\ln I_{\mathrm {C4}} \\[ 5pt ] \end{eqnarray}
\] となる。また，$\ln A +\ln B=\ln \left( AB\right)$となるから，
\[
\begin{eqnarray}
\ln I_{\mathrm {C1}}+\ln I_{\mathrm {C2}}&=&\ln I_{\mathrm {C3}}+\ln I_{\mathrm {C4}} \\[ 5pt ] \ln \left( I_{\mathrm {C1}} I_{\mathrm {C2}}\right)&=&\ln \left( I_{\mathrm {C3}} I_{\mathrm {C4}}\right) \\[ 5pt ] I_{\mathrm {C1}} I_{\mathrm {C2}}&=&I_{\mathrm {C3}} I_{\mathrm {C4}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
$ \ \mathrm {Q}_{3} \ $のコレクタ電流$ \ I_{\mathrm {C3}} \ $は各トランジスタのベース電流が零であるから，
\[
\begin{eqnarray}
I_{\mathrm {C3}}&=&I_{\mathrm {E3}} \\[ 5pt ] &=&I_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
$ \ I_{\mathrm {C1}}=I_{\mathrm {C2}}=I_{\mathrm {in}} \ $，$ \ I_{\mathrm {C3}}=I_{0} \ $，$ \ I_{\mathrm {C4}}=I_{\mathrm {out}} \ $を(3)解答式に代入すると，
\[
\begin{eqnarray}
I_{\mathrm {in}}^{2}&=&I_{0}I_{\mathrm {out}} \\[ 5pt ] I_{\mathrm {out}}&=&\frac {I_{\mathrm {in}}^{2}}{I_{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。