【問題】
【難易度】★★☆☆☆(やや易しい)
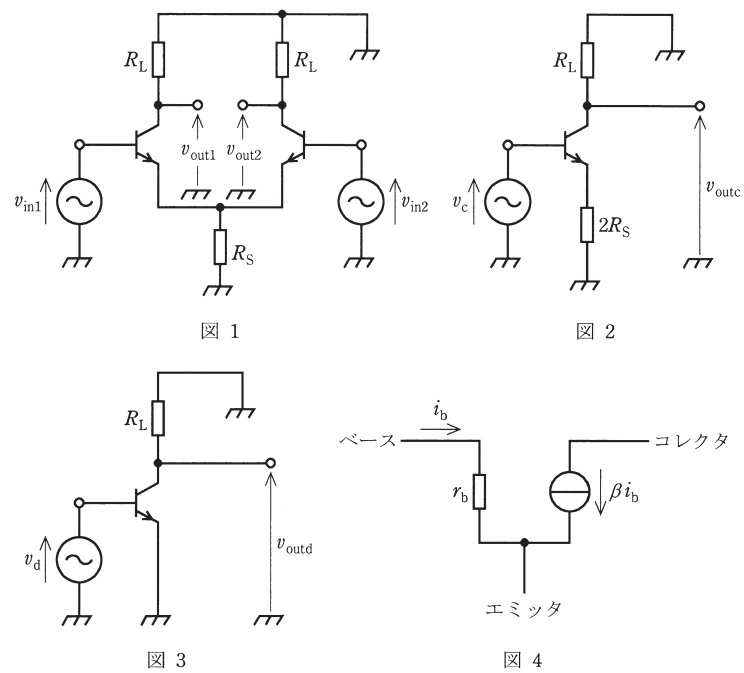
次の文章は,差動増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。ただし,図1から図3は交流成分のみを考慮しており,バイポーラトランジスタの交流等価回路は図4で表されるものとする。ここで,\( \ r_{\mathrm {b}} \ \)はエミッタを接地してベースからバイポーラトランジスタをみたときの抵抗値,\( \ \beta \ \)はエミッタ接地電流増幅率であり,ベース電流の\( \ \beta \ \)倍がコレクタ電流になることを表している。
図1の差動増幅回路において入力電圧\( \ v_{\mathrm {in1}} \ \)と\( \ v_{\mathrm {in2}} \ \)を
\[
\begin{eqnarray}
v_{\mathrm {in1}}&=&v_{\mathrm {c}}+v_{\mathrm {d}} \ &・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
v_{\mathrm {in2}}&=&v_{\mathrm {c}}-v_{\mathrm {d}} \ &・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
と表すことができる。ただし,\( \ v_{\mathrm {c}} \ \)と\( \ v_{\mathrm {d}} \ \)はそれぞれ同相入力電圧,差動入力電圧であり,
\[
\begin{eqnarray}
v_{\mathrm {c}}&=&\frac {v_{\mathrm {in1}}+v_{\mathrm {in2}}}{2} &・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
v_{\mathrm {d}}&=&\frac {v_{\mathrm {in1}}-v_{\mathrm {in2}}}{2} &・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
である。
\( \ v_{\mathrm {c}} \ \)だけが存在する場合は図2の回路を,\( \ v_{\mathrm {d}} \ \)だけが存在する場合は図3の回路をそれぞれ解析し,さらに重ね合わせの理を用いれば,\( \ v_{\mathrm {in1}} \ \)と\( \ v_{\mathrm {in2}} \ \)を入力した場合の解析結果を得ることができる。図2の出力電圧\( \ v_{\mathrm {outc}} \ \)は
\[
\begin{eqnarray}
v_{\mathrm {outc}}&=& \ \fbox { (1) } \ \times v_{\mathrm {c}} \ &・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
であり,図3の出力電圧\( \ v_{\mathrm {outd}} \ \)は
\[
\begin{eqnarray}
v_{\mathrm {outd}}&=& \ \fbox { (2) } \ \times v_{\mathrm {d}} \ &・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
である。これらの式に,\( \ R_{\mathrm {L}}=R_{\mathrm {S}}=1.0 \ \mathrm {[k\Omega ]} \ \),\( \ r_{\mathrm {b}}=5.0 \ \mathrm {[k\Omega ]} \ \),\( \ \beta =49 \ \)を代入し,重ね合わせの理を用いると,\( \ v_{\mathrm {in1}} \ \)と\( \ v_{\mathrm {in2}} \ \)を入力したとき,図1の\( \ v_{\mathrm {out1}} \ \)と\( \ v_{\mathrm {out2}} \ \)はそれぞれ
\[
\begin{eqnarray}
v_{\mathrm {out1}}&=& \ \fbox { (3) } \ \times v_{\mathrm {in1}}+ \ \fbox { (4) } \ \times v_{\mathrm {in2}} &・・・ ⑦& \\[ 5pt ]
v_{\mathrm {out2}}&=& \ \fbox { (4) } \ \times v_{\mathrm {in1}}+ \ \fbox { (3) } \ \times v_{\mathrm {in2}} &・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに,\( \ v_{\mathrm {out}}=v_{\mathrm {out1}}-v_{\mathrm {out2}} \ \)とすると,\( \ v_{\mathrm {out}} \ \)は
\[
\begin{eqnarray}
v_{\mathrm {out}}&=& \ \fbox { (5) } \ &・・・・・・・・・・・・・・・・ ⑨& \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& 9.8v_{\mathrm {in1}}-9.8v_{\mathrm {in2}} &(ロ)& -4.7 &(ハ)& \frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}+\left( 1+\beta \right) R_{\mathrm {S}}} \\[ 5pt ]
&(ニ)& 5.1 &(ホ)& -9.8v_{\mathrm {in1}}+9.8v_{\mathrm {in2}} &(ヘ)& -5.1 \\[ 5pt ]
&(ト)& \frac {-\beta R_{\mathrm {L}}}{2\left( 1+\beta \right) R_{\mathrm {S}}} &(チ)& \frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}} &(リ)& \frac {-\beta R_{\mathrm {L}}}{\left( 1+\beta \right) R_{\mathrm {S}}} \\[ 5pt ]
&(ヌ)& 9.8 &(ル)& 9.8v_{\mathrm {in1}}+9.8v_{\mathrm {in2}} &(ヲ)& 0.47 \\[ 5pt ]
&(ワ)& \frac {-\beta R_{\mathrm {L}}}{2r_{\mathrm {b}}+\left( 1+\beta \right) R_{\mathrm {S}}} &(カ)& 4.7 &(ヨ)& \frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}+2\left( 1+\beta \right) R_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
差動増幅回路に関する問題です。
一般的に差動増幅回路は図2や図3の等価回路が描けるかが最大のポイントとなりますが,本問はその等価回路が与えられているので,電子回路の基本知識を習得していればその場で考えて解ける問題となっています。
今後はどうなるか予想はできませんが,等価回路が与えられないとほとんどの受験生が解けなくなる可能性が高いので,差動増幅回路の場合は与えられると考えても良いかもしれません。
1.重ね合わせ(重ね)の理
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。
本問の場合は図1の回路に電流源がないので,図2と図3の結果をそのまま重ね合わせれば良いということになります。
【解答】
(1)解答:ヨ
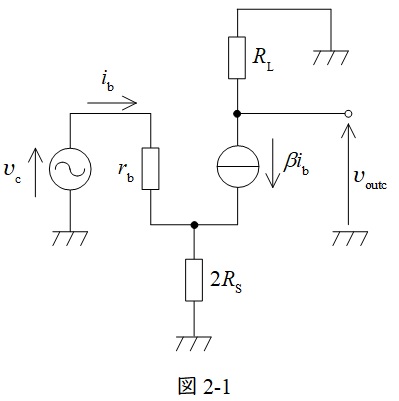
図2のトランジスタを図4の交流等価回路に置換えると図2-1の通りとなる。
図2-1の\( \ v_{\mathrm {c}} \ \)について,キルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
v_{\mathrm {c}} &=&r_{\mathrm {b}}i_{\mathrm {b}}+2R_{\mathrm {S}}\left( 1+\beta \right) i_{\mathrm {b}} \\[ 5pt ]
i_{\mathrm {b}}&=&\frac {v_{\mathrm {c}}}{r_{\mathrm {b}}+2\left( 1+\beta \right) R_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ v_{\mathrm {outc}} \ \)と\( \ R_{\mathrm {L}} \ \)についてキルヒホッフの法則を適用し,上式を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {outc}} &=&-\beta R_{\mathrm {L}}i_{\mathrm {b}} \\[ 5pt ]
&=&-\beta R_{\mathrm {L}}\cdot \frac {v_{\mathrm {c}}}{r_{\mathrm {b}}+2\left( 1+\beta \right) R_{\mathrm {S}}} \\[ 5pt ]
&=&\frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}+2\left( 1+\beta \right) R_{\mathrm {S}}}\times v_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
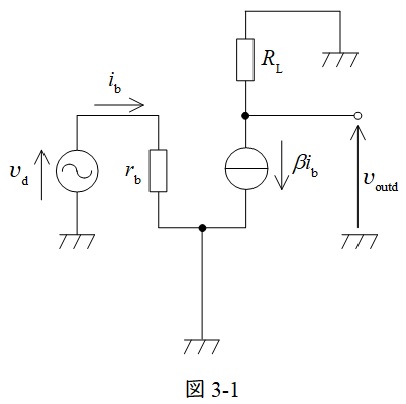
(1)と同様に図3のトランジスタを図4の交流等価回路に置換えると図3-1の通りとなる。
図3-1の\( \ v_{\mathrm {d}} \ \)について,キルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
v_{\mathrm {d}} &=&r_{\mathrm {b}}i_{\mathrm {b}} \\[ 5pt ]
i_{\mathrm {b}}&=&\frac {v_{\mathrm {d}}}{r_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ v_{\mathrm {outd}} \ \)と\( \ R_{\mathrm {L}} \ \)についてキルヒホッフの法則を適用し,上式を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {outd}} &=&-\beta R_{\mathrm {L}}i_{\mathrm {b}} \\[ 5pt ]
&=&-\beta R_{\mathrm {L}}\cdot \frac {v_{\mathrm {d}}}{r_{\mathrm {b}}} \\[ 5pt ]
&=&\frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}}\times v_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
(4)解答:カ
(1)及び(2)の解答式に各値を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {outc}} &=&\frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}+2\left( 1+\beta \right) R_{\mathrm {S}}}\times v_{\mathrm {c}} \\[ 5pt ]
&=&\frac {-49\times 1.0\times 10^{3}}{5.0\times 10^{3}+2\times \left( 1+49 \right) \times 1.0\times 10^{3}}\times v_{\mathrm {c}} \\[ 5pt ]
&≒&-0.46667\times v_{\mathrm {c}} \\[ 5pt ]
v_{\mathrm {outd}} &=&\frac {-\beta R_{\mathrm {L}}}{r_{\mathrm {b}}}\times v_{\mathrm {d}} \\[ 5pt ]
&=&\frac {-49\times 1.0\times 10^{3}}{5.0\times 10^{3}}\times v_{\mathrm {d}} \\[ 5pt ]
&=&-9.8\times v_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となり,これに③及び④を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {outc}} &=&-0.46667\times \frac {v_{\mathrm {in1}}+v_{\mathrm {in2}}}{2} \\[ 5pt ]
&≒&-0.23334 \left( v_{\mathrm {in1}}+v_{\mathrm {in2}}\right) \\[ 5pt ]
v_{\mathrm {outd}} &=&-9.8\times \frac {v_{\mathrm {in1}}-v_{\mathrm {in2}}}{2} \\[ 5pt ]
&=&-4.9\left( v_{\mathrm {in1}}-v_{\mathrm {in2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。重ね合わせの理より,\( \ v_{\mathrm {out1}} \ \)と\( \ v_{\mathrm {out2}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {out1}} &=&v_{\mathrm {outc}}+v_{\mathrm {outd}} \\[ 5pt ]
&=&-0.23334\left( v_{\mathrm {in1}}+v_{\mathrm {in2}}\right) -4.9\left( v_{\mathrm {in1}}-v_{\mathrm {in2}}\right) \\[ 5pt ]
&≒&-5.1333 v_{\mathrm {in1}}+4.6667v_{\mathrm {in2}} → -5.1v_{\mathrm {in1}}+4.7v_{\mathrm {in2}} \\[ 5pt ]
v_{\mathrm {out2}} &=&v_{\mathrm {outc}}-v_{\mathrm {outd}} \\[ 5pt ]
&=&-0.23334\left( v_{\mathrm {in1}}+v_{\mathrm {in2}}\right) +4.9\left( v_{\mathrm {in1}}-v_{\mathrm {in2}}\right) \\[ 5pt ]
&≒&4.6667 v_{\mathrm {in1}}-5.1333v_{\mathrm {in2}} → 4.7v_{\mathrm {in1}}-5.1v_{\mathrm {in2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
題意より,差動増幅回路の出力\( \ v_{\mathrm {out}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {out}} &=&v_{\mathrm {out1}}-v_{\mathrm {out2}} \\[ 5pt ]
&=&-5.1333 v_{\mathrm {in1}}+4.6667v_{\mathrm {in2}} -\left( 4.6667 v_{\mathrm {in1}}-5.1333v_{\mathrm {in2}}\right) \\[ 5pt ]
&=&-9.8 v_{\mathrm {in1}}+9.8v_{\mathrm {in2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん