【問題】
【難易度】★★★☆☆(普通)
次の文章は,真空中の電子電流に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
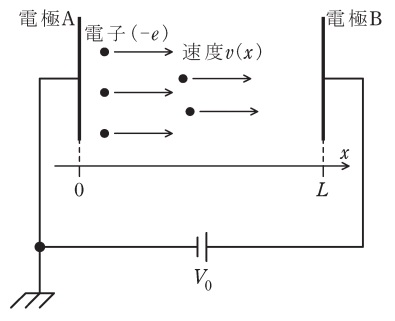
真空中で金属を加熱すると,熱エネルギーを得た電子が真空中に飛び出してくる熱電子放出を生じる。図は,電極\( \ \mathrm {A} \ \)から均一に熱電子が放出され,直流電圧\( \ V_{\mathrm {0}}\left( > 0 \right) \ \)によって,電極\( \ \mathrm {A} \ \)から距離\( \ L \ \)の位置にある電極\( \ \mathrm {B} \ \)に引き寄せられ,時間的に一定の電流密度\( \ J \ \)が流れている様子を表している。図中の\( \ x \ \)座標上の位置\( \ x \ \)における電子の平均速度を\( \ v\left( x \right) \ \),電荷密度を\( \ \rho \left( x \right) \ \)とし,電位を\( \ V\left( x \right) \ \)とする。ただし,\( \ V\left( 0 \right) =0 \ \),\( \ V\left( L \right) = V_{\mathrm {0}} \ \)と定める。簡単のため,電子の速度は\( \ x \ \)成分のみを持つものとし,また,電荷密度,電位は共に\( \ x \ \)軸に垂直な面内で一様であるものと仮定する。電極は十分広く,端部効果は無視するものとする。この時,位置\( \ x \ \)における電流密度\( \ J \ \)は,電子の速度\( \ v\left( x \right) \ \)と電荷密度\( \ \rho \left( x \right) \ \)を用いて,次のように表される。
\[
\begin{eqnarray}
J&=& \ \fbox { (1) } ・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
また,\( \ V\left( x \right) \ \)と\( \ \rho \left( x \right) \ \)の関係は,ポアソン方程式より以下のように表される。
\[
\begin{eqnarray}
\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}}&=&-\frac {\rho \left( x \right) }{\varepsilon _{0}} \ ・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ \varepsilon _{0} \ \)は真空の誘電率である。位置\( \ x \ \)における電子の運動エネルギーは,電子の質量\( \ m \ \)及び速度\( \ v\left( x \right) \ \)を用いて\( \ \ \fbox { (2) } \ \)と表される。放出直後の速度を\( \ v\left( 0 \right) =0 \ \)と近似すると,力学的エネルギー保存則より,
\[
\begin{eqnarray}
\fbox { (2) } \ &=&eV\left( x \right) \ ・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
が成り立つ。ただし,\( \ e \ \)は電気素量を表す。①~③式より\( \ v\left( x \right) \ \)と\( \ \rho \left( x \right) \ \)を消去すると,電流密度の大きさ\( \ \left| J \right| \ \)と,電位\( \ V\left( x \right) \ \)の関係は,次式で表される。
\[
\begin{eqnarray}
\left| J \right| &=& \ \fbox { (3) } \ \sqrt {V\left( x \right) }\left| \frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \right| ・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
定常状態では,\( \ J \ \)は位置\( \ x \ \)によらず一定でなければならない(電流連続)。また,放出される電子の数が増加すると,電極\( \ \mathrm {A} \ \)の近傍が負に帯電するため,\( \ x=0 \ \)における電界\( \ \displaystyle -\frac {\mathrm {d}V\left( x \right) }{\mathrm {d}x} \ \)が\( \ 0 \ \)に近づくことで電子放出が制限される。これらの条件を満たす電位分布は,\( \ \alpha \ \),\( \ \beta \ \)を正の実定数として,\( \ V\left( x \right) =\alpha x^{\beta } \ \)のように表され,④式が\( \ x \ \)によらない条件として\( \ x \ \)の指数部を零とすると,\( \ \beta = \ \fbox { (4) } \ \)と求められる。また,\( \ V\left( L \right) =\alpha L^{\beta } =V_{0} \ \)から\( \ \alpha \ \)が求まり,電流密度の大きさと印加電圧との関係として,\( \ \left| J \right| ∝ {V_{0}}^{\gamma } \ \),\( \ \gamma = \ \fbox { (5) } \ \)が導かれる。この関係は,熱電子放出電流を外部印加電圧により制御する基本原理となっている。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{2} &(ロ)& mv\left( x \right) &(ハ)& \frac {1}{2}\rho \left( x \right) {v\left( x \right) }^{2} \\[ 5pt ]
&(ニ)& \varepsilon _{0}\sqrt {\frac {2e}{m}} &(ホ)& \frac {2}{3} &(ヘ)& \frac {5}{3} \\[ 5pt ]
&(ト)& 2 &(チ)& \frac {1}{2}m {v\left( x \right) }^{2} &(リ)& \rho \left( x \right) v\left( x \right) \\[ 5pt ]
&(ヌ)& \varepsilon _{0}\sqrt {\frac {2m}{e}} &(ル)& \frac {4}{3} &(ヲ)& \frac {1}{2}m^{2} v\left( x \right) \\[ 5pt ]
&(ワ)& \frac {3}{2} &(カ)& \frac {1}{2}\rho \left( x \right) v\left( x \right) &(ヨ)& \sqrt {\frac {2\varepsilon _{0}}{m}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
真空中の電子の運動に関する問題のやや応用的な内容の問題です。
途中あまり電験では出題されないポアソンの方程式が出てきますが,(1)及び(2)の内容がわかっていると残りの空欄は計算問題となるので,知識レベルとしては特別高度な内容は使用しません。
文章が長く一見難しそうに見えるかもしれませんが,試験本番でも焦らない様,問題文や用語に騙されないようにしましょう。
1.電界中の電子の運動
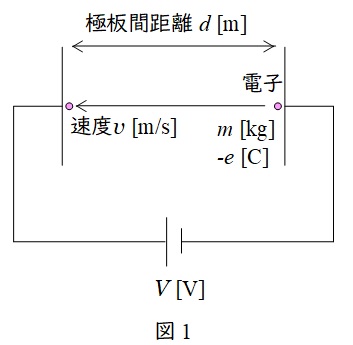
図1のように,極板間距離\( \ d \ \mathrm {[m]} \ \)の電極間に電圧\( \ V \ \mathrm {[V]} \ \)をかけたときの電子の運動を考えます。
まず,負極側にある電子について考えます。最初速度が零であるとすると,電子が受ける力\( \ F \ \mathrm {[N]} \ \)は,極板内の電界が\( \ \displaystyle E=\frac {V}{d} \ \mathrm {[V/m]} \ \)であるから,
\[
\begin{eqnarray}
F&=&eE \\[ 5pt ]
&=&\frac {eV}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。物体の運動方程式より,加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)とすると,\( \ F=ma \ \)の関係があるので,
\[
\begin{eqnarray}
a&=&\frac {F}{m} \\[ 5pt ]
&=&\frac {eV}{md} \\[ 5pt ]
\end{eqnarray}
\]
で加速されます。したがって,電子の加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)は電圧\( \ V \ \mathrm {[V]} \ \)に比例することが分かります。
次に,電子が距離\( \ d \ \mathrm {[m]} \ \)動き,反対側の電極に到達したときの電子の速度を考えます。負極にいるときの電子の位置エネルギーは\( \ eV \ \mathrm {[J]} \ \)であり,電子が正極に到達したときの運動エネルギーが\( \ \displaystyle W=\frac {1}{2}mv^{2} \ \mathrm {[J]} \ \)なので,エネルギー保存の法則により位置エネルギーがすべて運動エネルギーになったとすると,
\[
\begin{eqnarray}
eV&=&\frac {1}{2}mv^{2} \\[ 5pt ]
v^{2}&=&\frac {2eV}{m} \\[ 5pt ]
v&=&\sqrt {\frac {2eV}{m}} \\[ 5pt ]
\end{eqnarray}
\]
になります。
【解答】
(1)解答:リ
単位面積あたりの電流(電荷の流れ)が電流密度\( \ J \ \),単位体積あたりの電荷の密度が電荷密度\( \ \rho \left( x \right) \ \)なので,電流の流れる面積を\( \ S \ \)とすると,電流を求める式の関係から,
\[
\begin{eqnarray}
JS&=&\rho \left( x \right) Sv\left( x \right) \\[ 5pt ]
J&=&\rho \left( x \right) v\left( x \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
ワンポイント解説「1.電界中の電子の運動」より,電子の運動エネルギー\( \ W \ \)は
\[
\begin{eqnarray}
W&=&\frac {1}{2}m {v\left( x \right) }^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,エネルギー保存則より,
\[
\begin{eqnarray}
\frac {1}{2}m {v\left( x \right) }^{2}&=&eV\left( x \right) \\[ 5pt ]
\end{eqnarray}
\]
の関係が成り立つ。
(3)解答:ニ
②より,
\[
\begin{eqnarray}
\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}}&=&-\frac {\rho \left( x \right) }{\varepsilon _{0}} \\[ 5pt ]
\rho \left( x \right) &=&-\varepsilon _{0}\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,③より,
\[
\begin{eqnarray}
\frac {1}{2}m {v\left( x \right) }^{2}&=&eV\left( x \right) \\[ 5pt ]
{v\left( x \right) }^{2}&=&\frac {2eV\left( x \right) }{m} \\[ 5pt ]
v\left( x \right) &=&\sqrt {\frac {2eV\left( x \right) }{m}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,それぞれ①に代入すると,
\[
\begin{eqnarray}
J&=&\rho \left( x \right) v\left( x \right) \\[ 5pt ]
&=&-\varepsilon _{0}\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}}\cdot \sqrt {\frac {2eV\left( x \right) }{m}} \\[ 5pt ]
&=&-\varepsilon _{0}\sqrt {\frac {2eV\left( x \right) }{m}}\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電流密度の大きさ\( \ \left| J \right| \ \)は,
\[
\begin{eqnarray}
\left| J \right| &=&\varepsilon _{0}\sqrt {\frac {2eV\left( x \right) }{m}}\left| \frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \right| \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\sqrt {V\left( x \right) }\left| \frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \right| \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ V\left( x \right) =\alpha x^{\beta } \ \)とすると,
\[
\begin{eqnarray}
\frac {\mathrm {d}V\left( x \right) }{\mathrm {d}x} &=&\alpha \beta x^{\beta -1} \\[ 5pt ]
\frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}}&=&\alpha \beta \left( \beta -1\right) x^{\beta -2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,④に代入すると,
\[
\begin{eqnarray}
\left| J \right| &=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\sqrt {V\left( x \right) }\left| \frac {\mathrm {d}^{2}V\left( x \right) }{\mathrm {d}x^{2}} \right| \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\sqrt {\alpha x^{\beta }}\left| \alpha \beta \left( \beta -1\right) x^{\beta -2} \right| \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\sqrt {\alpha x^{\beta }} \alpha \beta \left( \beta -1\right) x^{\beta -2} \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\alpha ^{\frac {3}{2}} \beta \left( \beta -1\right) x^{\frac {\beta }{2}+\beta -2} \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\alpha ^{\frac {3}{2}} \beta \left( \beta -1\right) x^{\frac {3\beta }{2}-2} ・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となる。上式が\( \ x \ \)によらない条件として\( \ x \ \)の指数部を零とすると,
\[
\begin{eqnarray}
\frac {3\beta }{2}-2&=&0 \\[ 5pt ]
\frac {3\beta }{2}&=&2 \\[ 5pt ]
\beta &=&\frac {4}{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ワ
\( \ V\left( L \right) =\alpha L^{\frac {4}{3} } =V_{0} \ \)より,
\[
\begin{eqnarray}
\alpha &=&V_{0}L^{-\frac {4}{3} } \\[ 5pt ]
\end{eqnarray}
\]
であるから,⑤式は,
\[
\begin{eqnarray}
\left| J \right| &=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\alpha ^{\frac {3}{2}} \beta \left( \beta -1\right) x^{\frac {3\beta }{2}-2} \\[ 5pt ]
&=&\varepsilon _{0}\sqrt {\frac {2e}{m}}\left( V_{0}L^{-\frac {4}{3} }\right) ^{\frac {3}{2}}\times \frac {4}{3} \times \left( \frac {4}{3} -1\right) \cdot 1 \\[ 5pt ]
&=&\frac {4}{9}\varepsilon _{0}\sqrt {\frac {2e}{m}}V_{0}^{\frac {3}{2}}L^{-2 } \\[ 5pt ]
&∝&V_{0}^{\frac {3}{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \gamma = \frac {3}{2} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん