《理論》〈電子理論〉[R07:問7]自己バイアス増幅回路の特性に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

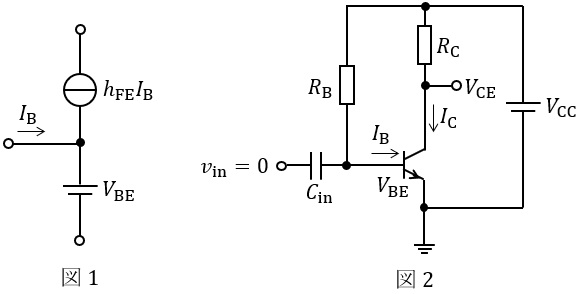
次の文章は，エミッタ接地増幅回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，$ \ \mathrm {npn} \ $トランジスタの直流等価回路は図1で表せるとする。図2及び図3に示すエミッタ接地増幅回路はいずれも入力電圧を加えない状態（$ \ v_{\mathrm {in}}=0 \ $）とし，そのバイアス電流及び電圧について考える。

図2の回路において，トランジスタのベース・エミッタ間電圧$ \ V_{\mathrm {BE}} \ $を用いてベース電流を求め，トランジスタの直流における電流増幅率$ \ h_{\mathrm {FE}} \ $を用いてコレクタ電流を求めると$ \ \fbox {　（１）　} \ $が得られる。このため，図2のコレクタ・エミッタ間電圧$ \ V_{\mathrm {CE}} \ $は$ \ \fbox {　（２）　} \ $となる。

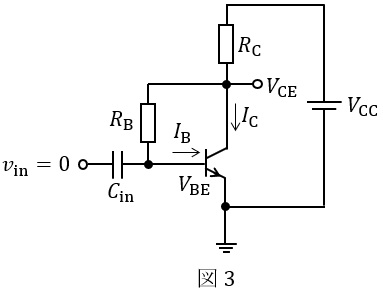
一方，図3のベース電流はコレクタ・エミッタ間電圧$ \ V_{\mathrm {CE}} \ $を用いて$ \ \fbox {　（３）　} \ $と表せる。$ \ I_{\mathrm {B}}≪I_{\mathrm {C}} \ $のとき$ \ R_{\mathrm {C}} \ $を流れる電流は$ \ I_{\mathrm {C}} \ $と近似できることを用いて，図3のコレクタ・エミッタ間電圧$ \ V_{\mathrm {CE}} \ $を求めると$ \ \fbox {　（４）　} \ $となる。

以上の結果を用いて，$ \ V_{\mathrm {CC}}=20 \ \mathrm {V} \ $，$ \ V_{\mathrm {BE}}=0.6 \ \mathrm {V} \ $，$ \ R_{\mathrm {C}}=1 \ \mathrm {k\Omega } \ $，$ \ h_{\mathrm {FE}}=200 \ $であるとき図2及び図3において$ \ V_{\mathrm {CE}}=10 \ \mathrm {V} \ $となるように$ \ R_{\mathrm {B}} \ $を定める。図2の$ \ R_{\mathrm {B}} \ $は$ \ 388 \ \mathrm {k\Omega } \ $となり，図3の$ \ R_{\mathrm {B}} \ $は$ \ \fbox {　（５）　} \ \mathrm {k\Omega } \ $となる。この状態でそれぞれの回路の$ \ h_{\mathrm {FE}} \ $が$ \ 200 \ $から$ \ 220 \ $に変化したとき，図2の$ \ V_{\mathrm {CE}} \ $は$ \ 9.0 \ \mathrm {V} \ $となるのに対して，図3の$ \ V_{\mathrm {CE}} \ $はおよそ$ \ \fbox {　（６）　} \ \mathrm {V} \ $となるため，図3の方が$ \ h_{\mathrm {FE}} \ $の変動がバイアス電位に与える影響を抑えることができる構成といえる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　9.24　　　　　&（ロ）&　9.54　　　　　&（ハ）&　9.84 \\[ 5pt ] &（ニ）&　88　　　　　&（ホ）&　188　　　　　&（ヘ）&　288 \\[ 5pt ] &（ト）&　\frac {V_{\mathrm {CE}}}{R_{\mathrm {C}}}　　　　　&（チ）&　R_{\mathrm {C}}\frac {h_{\mathrm {FE}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}}　　　　　&（リ）&　V_{\mathrm {CC}}-h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {BE}} \\[ 5pt ] &（ヌ）&　\frac {V_{\mathrm {CE}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}}　　　　　&（ル）&　\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}}　　　　　&（ヲ）&　\frac {V_{\mathrm {BE}}-V_{\mathrm {CE}}}{R_{\mathrm {B}}} \\[ 5pt ] &（ワ）&　h_{\mathrm {FE}}\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}}　　　　　&（カ）&　h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) 　　　　　&（ヨ）&　h_{\mathrm {FE}}\frac {V_{\mathrm {CE}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（タ）&　V_{\mathrm {CC}}-R_{\mathrm {C}}\frac {h_{\mathrm {FE}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}} \\[ 5pt ] &（レ）&　V_{\mathrm {CC}}-h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) \\[ 5pt ] &（ソ）&　V_{\mathrm {CC}}-R_{\mathrm {C}}\frac {h_{\mathrm {FE}}V_{\mathrm {BE}} }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

エミッタ接地増幅回路の回路演算に関する問題です。
(4)の計算に少しテクニックが必要となりますが，解法パターンはほぼ決まっているので，ぜひマスターして得点源とできるようにしましょう。
特に$ \ 1 \ $種の場合は選択問題の配点が高くなるので，電子回路を理解すると科目合格にグッと近づくことになります。

【解答】

(1)解答：ワ
図2-1に示す閉回路に着目すると，$ \ R_{\mathrm {B}} \ $を流れる電流は$ \ I_{\mathrm {B}} \ $であり，$ \ R_{\mathrm {B}} \ $に加わる電圧が$ \ V_{\mathrm {CC}}-V_{\mathrm {BE}} \ $なので，
\[
\begin{eqnarray}
I_{\mathrm {B}} &=&\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] となる。よって，電流増幅率が$ \ h_{\mathrm {FE}} \ $なので，コレクタ電流$ \ I_{\mathrm {C}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {C}} &=&h_{\mathrm {FE}}I_{\mathrm {B}} \\[ 5pt ] &=&h_{\mathrm {FE}}\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

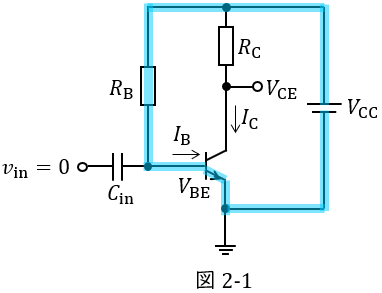
(2)解答：レ
図2-2に示す閉回路に着目すると，コレクタ・エミッタ間電圧$ \ V_{\mathrm {CE}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {CE}} &=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ] &=&V_{\mathrm {CC}}-R_{\mathrm {C}}h_{\mathrm {FE}}\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] &=&V_{\mathrm {CC}}-h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

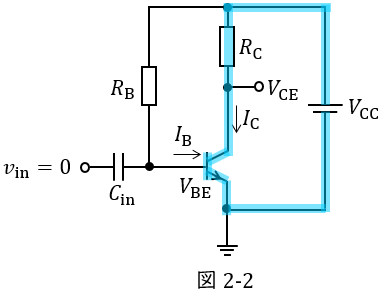
(3)解答：ヌ
図3においても(1)と同様に，$ \ R_{\mathrm {B}} \ $を流れる電流は$ \ I_{\mathrm {B}} \ $であり，$ \ R_{\mathrm {B}} \ $に加わる電圧が$ \ V_{\mathrm {CE}}-V_{\mathrm {BE}} \ $なので，
\[
\begin{eqnarray}
I_{\mathrm {B}} &=&\frac {V_{\mathrm {CE}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：タ
(3)解答式より，電流増幅率が$ \ h_{\mathrm {FE}} \ $なので，コレクタ電流$ \ I_{\mathrm {C}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {C}} &=&h_{\mathrm {FE}}I_{\mathrm {B}} \\[ 5pt ] &=&h_{\mathrm {FE}}\frac {V_{\mathrm {CE}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
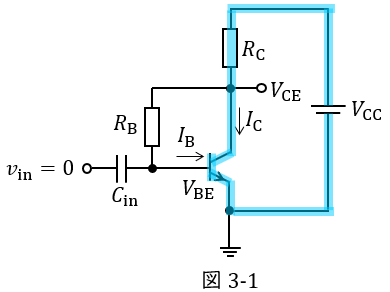
\] となり，図3-1に示す閉回路に着目すると，コレクタ・エミッタ間電圧$ \ V_{\mathrm {CE}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {CE}} &=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ] &=&V_{\mathrm {CC}}-R_{\mathrm {C}}h_{\mathrm {FE}}\frac {V_{\mathrm {CE}}-V_{\mathrm {BE}}}{R_{\mathrm {B}}} \\[ 5pt ] &=&V_{\mathrm {CC}}-h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}\left( V_{\mathrm {CE}}-V_{\mathrm {BE}}\right) \\[ 5pt ] &=&V_{\mathrm {CC}}-h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {CE}}+h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {BE}} \\[ 5pt ] V_{\mathrm {CE}}+h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {CE}}&=&V_{\mathrm {CC}}+h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {BE}} \\[ 5pt ] \left( 1+h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}\right) V_{\mathrm {CE}}&=&V_{\mathrm {CC}}+h_{\mathrm {FE}}\frac {R_{\mathrm {C}}}{R_{\mathrm {B}}}V_{\mathrm {BE}} \\[ 5pt ] \left( R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}\right) V_{\mathrm {CE}}&=&R_{\mathrm {B}}V_{\mathrm {CC}}+h_{\mathrm {FE}}R_{\mathrm {C}}V_{\mathrm {BE}} \\[ 5pt ] V_{\mathrm {CE}}&=&\frac {R_{\mathrm {B}}V_{\mathrm {CC}}+h_{\mathrm {FE}}R_{\mathrm {C}}V_{\mathrm {BE}}}{R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}} \\[ 5pt ] &=&\frac {\left( R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}\right) V_{\mathrm {CC}}-h_{\mathrm {FE}}R_{\mathrm {C}}V_{\mathrm {CC}}+h_{\mathrm {FE}}R_{\mathrm {C}}V_{\mathrm {BE}}}{R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}} \\[ 5pt ] &=&\frac {\left( R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}\right) V_{\mathrm {CC}}-h_{\mathrm {FE}}R_{\mathrm {C}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}}R_{\mathrm {C}}} \\[ 5pt ] &=&V_{\mathrm {CC}}-R_{\mathrm {C}}\frac {h_{\mathrm {FE}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
(4)解答式に各値を代入すると，
\[
\begin{eqnarray}
V_{\mathrm {CE}} &=&V_{\mathrm {CC}}-R_{\mathrm {C}}\frac {h_{\mathrm {FE}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}} \\[ 5pt ] 10 &=&20-1 \ 000 \times \frac {200\times \left( 20-0.6\right) }{R_{\mathrm {B}}+200\times 1 \ 000} \\[ 5pt ] 10 &=&20-1 \ 000 \times \frac {3 \ 880}{R_{\mathrm {B}}+200 \ 000} \\[ 5pt ] 1 \ 000 \times \frac {3 \ 880}{R_{\mathrm {B}}+200 \ 000}&=&10 \\[ 5pt ] \frac {3 \ 880}{R_{\mathrm {B}}+200 \ 000}&=&0.01 \\[ 5pt ] R_{\mathrm {B}}+200 \ 000&=&388 \ 000 \\[ 5pt ] R_{\mathrm {B}}&=&188 \ 000 \ \mathrm {[\Omega ]}　→　188 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)解答：ロ
(4)解答式に各値を代入すると，
\[
\begin{eqnarray}
V_{\mathrm {CE}} &=&V_{\mathrm {CC}}-R_{\mathrm {C}}\frac {h_{\mathrm {FE}}\left( V_{\mathrm {CC}}-V_{\mathrm {BE}}\right) }{R_{\mathrm {B}}+h_{\mathrm {FE}} R_{\mathrm {C}}} \\[ 5pt ] &=&20-1 \ 000 \times \frac {220\times \left( 20-0.6\right) }{188 \ 000+220\times 1 \ 000} \\[ 5pt ] &≒&20-10.461 \\[ 5pt ] &≒&9.54 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。