Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,誘電体境界面における電気力線の屈折に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
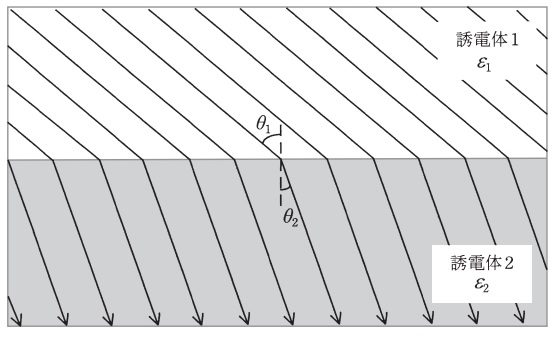
図のように,誘電率の異なる誘電体\( \ 1 \ \)及び\( \ 2 \ \)が平面を境界として接している。その誘電率はそれぞれ\( \ \varepsilon _{1} \ \),\( \ \varepsilon _{2} \ \)であり,境界面とその近傍の誘電体に真電荷は存在しない。この境界面に対し,誘電体\( \ 1 \ \)側から角度\( \ \theta _{1} \ \)で斜めに入射した一様な電気力線はそこで屈折し,角度\( \ \theta _{2} \ \)で誘電体\( \ 2 \ \)に入り込む。ただし,\( \ 0 < \theta _{1} < 90° \ \),\( \ 0 < \theta _{2} < 90° \ \)とする。 誘電体\( \ 1 \ \)及び\( \ 2 \ \)の電束密度の大きさをそれぞれ\( \ D_{1} \ \)及び\( \ D_{2} \ \)とし,電界の大きさをそれぞれ\( \ E_{1} \ \)及び\( \ E_{2} \ \)とすると, \[ \begin{eqnarray} D_{1}&=&\fbox { (1) } \ E_{1} \\[ 5pt ] D_{2}&=&\fbox { (2) } \ E_{2} \\[ 5pt ] \end{eqnarray} \] である。次に,真電荷が存在しないことを考慮すると,ガウスの法則により,境界面に対する電束密度の垂直成分は等しく, \[ \begin{eqnarray} \fbox { (3) } \\[ 5pt ] \end{eqnarray} \] が成り立つ。さらに,境界面上の任意の点において誘電体1及び2の電位は同じであるため,電界の境界面に平行な成分は等しく, \[ \begin{eqnarray} E_{1}\sin \theta _{1}&=&E_{2}\sin \theta _{2} \\[ 5pt ] \end{eqnarray} \] が成り立つ。これにより,\( \ \theta _{1} \ \),\( \ \theta _{2} \ \),\( \ \varepsilon _{1} \ \)及び\( \ \varepsilon _{2} \ \)の関係式が \[ \begin{eqnarray} \fbox { (4) } \\[ 5pt ] \end{eqnarray} \] のように求められる。 \( \ \theta _{1} > \theta _{2} \ \)のとき,\( \ D_{1} \ \)と\( \ D_{2} \ \)の大小関係,\( \ E_{1} \ \)と\( \ E_{2} \ \)の大小関係は,それぞれ\( \ \fbox { (5) } \ \)である。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& D_{1} > D_{2},E_{1} < E_{2} &(ロ)& \varepsilon _{2} &(ハ)& D_{1}\sin \theta _{1}=D_{2}\sin \theta _{2} \\[ 5pt ]
&(ニ)& \frac {\cos \theta _{2}}{\cos \theta _{1}}=\frac {\varepsilon _{2}}{\varepsilon _{1}} &(ホ)& D_{1}\tan \theta _{1}=D_{2}\tan \theta _{2} &(ヘ)& \frac {\varepsilon _{1}+\varepsilon _{2}}{2} \\[ 5pt ]
&(ト)& \varepsilon _{1} &(チ)& \frac {\tan \theta _{2}}{\tan \theta _{1}}=\frac {\varepsilon _{2}}{\varepsilon _{1}} &(リ)& \sqrt {\varepsilon _{1}\varepsilon _{2}} \\[ 5pt ]
&(ヌ)& D_{1} = D_{2},E_{1} < E_{2} &(ル)& D_{1}\tan \theta _{2}=D_{2}\tan \theta _{1} &(ヲ)& D_{1} < D_{2},E_{1} > E_{2} \\[ 5pt ]
&(ワ)& D_{1}\cos \theta _{1}=D_{2}\cos \theta _{2} &(カ)& \frac {\sin \theta _{2}}{\sin \theta _{1}}=\frac {\varepsilon _{2}}{\varepsilon _{1}} &(ヨ)& D_{1} = D_{2}
\end{eqnarray}
\]
【ワンポイント解説】
電束密度\( \ D \ \)と電界の大きさ\( \ E \ \)の関係式と三角関数の数学を使用します。さほど難易度が高い問題ではありませんが,似たような選択肢が多いので,ケアレスミスに注意して慎重に解く必要があります。
1.電束密度\( \ D \ \)と電界の大きさ\( \ E \ \)の関係式
電束密度\( \ D \ \)と電界の大きさ\( \ E \ \)は,空間の誘電率を\( \ \varepsilon \ \)とすると,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.三角関数の公式
三角関数の基本公式として,
\[
\begin{eqnarray}
\tan \theta &=&\frac {\sin \theta}{\cos \theta} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ト
(2)解答:ロ
ワンポイント解説の「1.電束密度\( \ D \ \)と電界の大きさ\( \ E \ \)の関係式」より,
\[
\begin{eqnarray}
D_{1} &=&\varepsilon _{1}E_{1} &・・・・・・・・・・・・ ①& \\[ 5pt ]
D_{2} &=&\varepsilon _{2}E_{2} &・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ワ
誘電体\( \ 1 \ \)での電束密度の垂直成分は,\( \ D_{1}\cos \theta _{1} \ \),誘電体\( \ 2 \ \)での電束密度の垂直成分は,\( \ D_{2}\cos \theta _{2} \ \)となるので,その垂直成分は等しいから,
\[
\begin{eqnarray}
D_{1}\cos \theta _{1}&=&D_{2}\cos \theta _{2} &・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。
(4)解答:チ
①,②を③に代入すると,
\[
\begin{eqnarray}
\varepsilon _{1}E_{1}\cos \theta _{1}&=&\varepsilon _{2}E_{2}\cos \theta _{2} \ &・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となる。また,題意より,
\[
\begin{eqnarray}
E_{1}\sin \theta _{1}&=&E_{2}\sin \theta _{2} &・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
であるから,⑤\( \ \div \ \)④より,
\[
\begin{eqnarray}
\frac{\sin \theta _{1}}{\varepsilon _{1}\cos \theta _{1}} &=& \frac{\sin \theta _{2}}{\varepsilon _{2}\cos \theta _{2}} \\[ 5pt ]
\frac{\tan \theta _{1}}{\varepsilon _{1}} &=& \frac{\tan \theta _{2}}{\varepsilon _{2}} \\[ 5pt ]
\frac{\varepsilon _{2}}{\varepsilon _{1}} &=& \frac{\tan \theta _{2}}{\tan \theta _{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
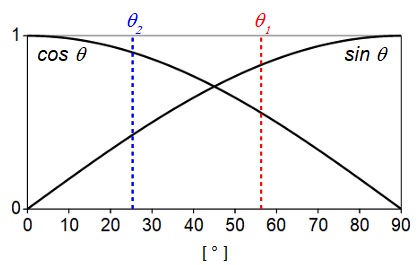
下図より\( \ 0 < \theta < 90° \ \)においては,
\[
\begin{eqnarray}
\sin \theta_{1} > \sin \theta_{2} 及び\cos \theta_{1} < \cos \theta_{2} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。③と⑤を変形すると,
\[
\begin{eqnarray}
\frac {D_{1}}{D_{2}}&=&\frac {\cos \theta _{2} }{\cos \theta _{1}} >1 &・・・・・・ ③^{\prime }& \\[ 5pt ]
\frac {E_{1}}{E_{2}}&=&\frac {\sin \theta _{2} }{\sin \theta _{1}} <1 &・・・・・・ ⑤^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となるから,解答は,\( \ D_{1} > D_{2},E_{1} < E_{2} \ \)となる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは