Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
図1に示すように,抵抗,コンデンサ,直流電流源,スイッチからなる回路を考える。初期状態ではスイッチが開いており回路は定常状態にあるものとする。時刻\( \ t=0 \ \)でスイッチを閉じた後スイッチを通過する電流\( \ i \ \)の変化について考察する。
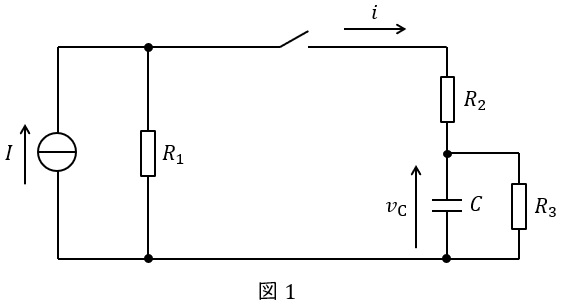
スイッチを入れる前の初期状態においてコンデンサ\( \ C \ \)の電圧\( \ v_{\mathrm {C}} \ \)は\( \ \fbox { (1) } \ \)である。スイッチを入れた直後に流れる電流\( \ i(0) \ \)は\( \ R_{3} \ \)とは無関係であり,次のように計算できる。
\[
\begin{eqnarray}
i(0) &=& \ \fbox { (2) } \ \\[ 5pt ]
\end{eqnarray}
\]
その後コンデンサ\( \ C \ \)には電流が流入して徐々に電圧が増加するが,電圧が増加すればするほど電流の流入は少なくなり,やがて定常状態に達する。定常状態ではコンデンサ\( \ C \ \)の電圧は一定で電流は流れないので,\( \ R_{2} \ \)の電流は全て\( \ R_{3} \ \)に流れる。スイッチ右側の負荷は抵抗\( \ R_{2} \ \)と\( \ \fbox { (3) } \ \)の直列接続であるので,定常状態でスイッチを流れる電流\( \ i(\infty ) \ \)は
\[
\begin{eqnarray}
i(\infty ) &=& \ \fbox { (4) } \ \\[ 5pt ]
\end{eqnarray}
\]
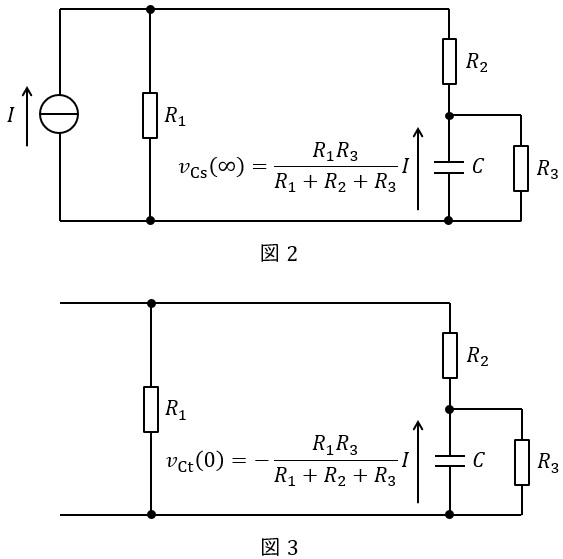
以下,コンデンサ\( \ C \ \)の充電時定数\( \ \tau \ \)について考える。\( \ v_{\mathrm {C}} \ \)は,定常項\( \ v_{\mathrm {Cs}} \ \)(図2参照)と過渡項\( \ v_{\mathrm {Ct}} \ \)(図3参照)を足し合わせたものである。このうち\( \ v_{\mathrm {Cs}} \ \)は時間的に変化せず,\( \ v_{\mathrm {Ct}} \ \)の時定数は\( \ \tau \ \)である。過渡項は「定常状態(図2)の\( \ C \ \)の電圧\( \ v_{\mathrm {Cs}}( \infty ) \ \)と同じ大きさで極性が逆向きの電圧\( \ v_{\mathrm {Ct}} ( 0 ) \ \)」が\( \ C \ \)に生じている状態(図3:左端の電流源は開放)から開始される放電現象であるから,その時定数\( \ \tau \ \)は容量\( \ C \ \)と,図3において\( \ C \ \)の両端から見た等価抵抗\( \ \fbox { (5) } \ \)の積で与えられる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& R_{1} &(ロ)& R_{3} &(ハ)& 0 \\[ 5pt ]
&(ニ)& IR_{1} &(ホ)& IR_{3} &(ヘ)& C \\[ 5pt ]
&(ト)& \frac {R_{3} ( R_{1}+R_{2} )}{R_{1}+R_{2}+R_{3}} &(チ)& \frac {R_{1} ( R_{2}+R_{3} )}{R_{1}+R_{2}+R_{3}} &(リ)& \frac {R_{1}R_{2}R_{3}}{R_{2}R_{3}+R_{3}R_{1}+R_{1}R_{2}} \\[ 5pt ]
&(ヌ)& \frac {R_{1}}{R_{1}+R_{2}}I &(ル)& \frac {R_{2}}{R_{1}+R_{2}}I &(ヲ)& \frac {R_{1}R_{2}}{R_{1}+R_{2}}I \\[ 5pt ]
&(ワ)& \frac {CR_{1}}{R_{1}+R_{2}+R_{3}}I &(カ)& \frac {R_{1}}{R_{1}+R_{2}+R_{3}}I &(ヨ)& \frac {R_{2}+R_{3}}{R_{1}+R_{2}+R_{3}}I \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電流源と抵抗,コンデンサを組み合わせた回路の過渡現象に関する問題です。
例年微分方程式を解く問題が出題されますが,本問は微分方程式ではなく,文章を読み解きながら正答を導いていく問題でした。
計算量もあまり多くないため,できれば高得点を狙いたい問題です。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチをオンまたはオフした直後の解で,直前の電圧や電流から変化する時の解です。
【解答】
(1)解答:ハ
スイッチを入れる前の初期状態において,コンデンサ\( \ C \ \)に蓄えられている電荷は\( \ 0 \ \)であり,\( \ Q=CV \ \)の関係から初期状態でのコンデンサ\( \ C \ \)の電圧\( \ v_{\mathrm {C}} \ \)は\( \ 0 \ \)となる。
(2)解答:ヌ
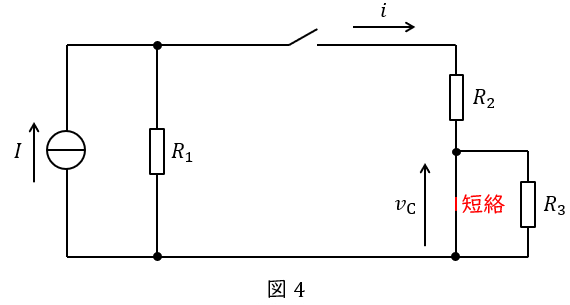
スイッチを入れた直後はコンデンサはほぼ短絡と考えれば良いので,回路図は図4のようになる。したがって,\( \ R_{3} \ \)は無視して良く,電流\( \ i(0) \ \)は分流の法則より,
\[
\begin{eqnarray}
i(0) &=&\frac {R_{1}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
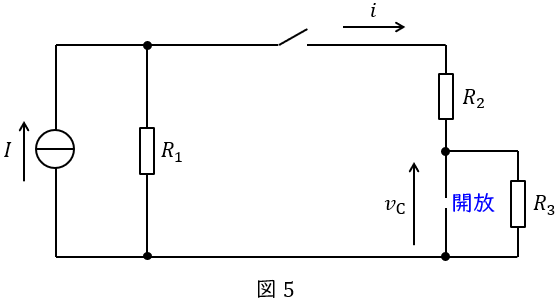
定常状態ではコンデンサ\( \ C \ \)は開放と考えればよく,回路図は図5のようになる。したがって,スイッチ右側の負荷は抵抗\( \ R_{2} \ \)と\( \ R_{3} \ \)の直列接続となる。
(4)解答:カ
図5より,定常状態でスイッチを流れる電流\( \ i(\infty ) \ \)は,分流の法則より,
\[
\begin{eqnarray}
i(\infty ) &=& \frac {R_{1}}{R_{1}+R_{2}+R_{3}}I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ト
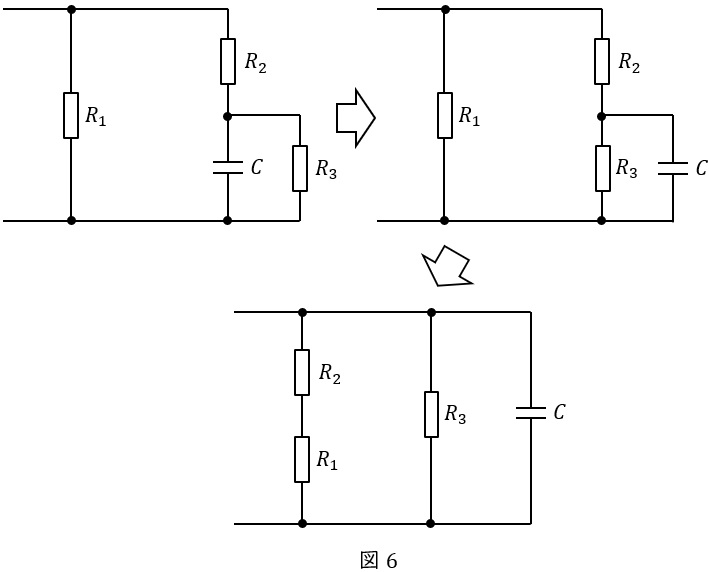
図3において\( \ C \ \)の両端から見た等価抵抗を求めるため,回路を変形すると図6のようになる。図6より,\( \ C \ \)の両端から見た等価抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R &=& \frac {R_{3} ( R_{1}+R_{2} )}{R_{1}+R_{2}+R_{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは