【問題】
【難易度】★★★☆☆(普通)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
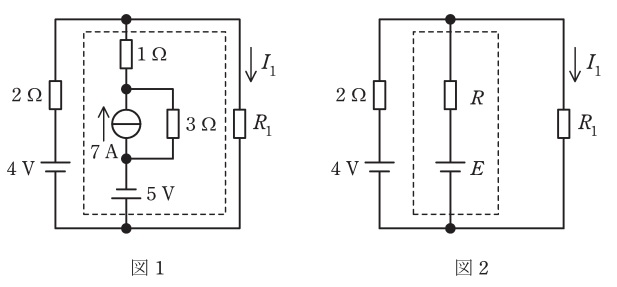
図1のように電流源,電圧源及び抵抗を接続した回路がある。図1の破線で囲まれた部分を図2の破線部分に示す抵抗\( \ R \ \)と電圧源\( \ E \ \)に等価変換すると,\( \ R= \ \fbox { (1) } \ \mathrm {\Omega} \ \),\( \ E= \ \fbox { (2) } \ \mathrm {V} \ \)となる。
図2から,抵抗\( \ R_{1} \ \)に流れる電流\( \ I_{1} \ \)を求めると,\( \ I_{1}= \ \fbox { (3) } \ \mathrm {[A]} \ \)となる。また,\( \ R_{1} \ \)で消費される電力\( \ P \ \)は\( \ P={I_{1}}^{2}R_{1} \ \)で求められる。
したがって,\( \ R_{1}= \ \fbox { (4) } \ \mathrm {\Omega } \ \)のときに電力\( \ P \ \)は最大となり,\( \ P= \ \fbox { (5) } \ \mathrm {W} \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 9 &(ロ)& 5 &(ハ)& 8.3 \\[ 5pt ]
&(ニ)& \frac {4}{3} &(ホ)& 6 &(ヘ)& \frac {24}{3R_{1}+4} \\[ 5pt ]
&(ト)& \frac {3}{4} &(チ)& \frac {5}{3R_{1}+4} &(リ)& 44.2 \\[ 5pt ]
&(ヌ)& 2 &(ル)& 16 &(ヲ)& 12.0 \\[ 5pt ]
&(ワ)& \frac {-5}{3R_{1}+4} &(カ)& \frac {1}{3} &(ヨ)& 4 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直流回路の回路計算の問題です。
\( \ 3 \ \)種の頃よりも回路は複雑になりますが,解き方は基本的に同じです。
(3)を求める際,重ね合わせの理やミルマンの定理等,複数の方法が考えられますが,どの方法でも正答が出れば大丈夫です。
本問のレベルは普通としていますが,\( \ 2 \ \)種の受験生だとすると,多くの受験生が完答してくると思っておいて良いと思います。
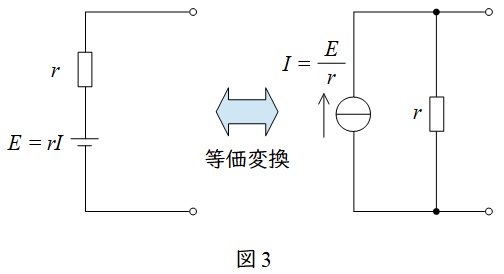
1.電圧源と電流源の等価変換
図3に示すように,電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
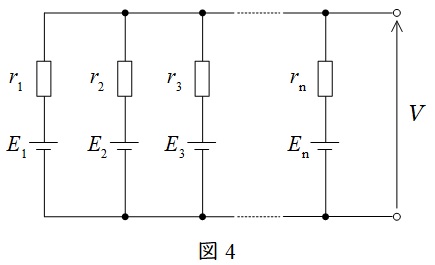
2.ミルマンの定理
図4のような,電源\( \ E_{1},E_{2},\cdots ,E_{\mathrm {n}} \ \)と抵抗\( \ r_{1},r_{2},\cdots ,r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
3.テブナンの定理
問題図において,回路中の\( \ R_{1} \ \)を開放したときの開放電圧を\( \ V_{0} \ \),電圧源を短絡し,電流源を開放した時の\( \ R_{1} \ \)から見た合成抵抗を\( \ R_{0} \ \)とした時,\( \ R_{1} \ \)を流れる電流\( \ I \ \)は,下式の通りとなります。
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R_{0}+R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
重ね合わせの理の証明
鳳・テブナンの定理の証明
ミルマンの定理の導出
【解答】
(1)解答:ヨ
ワンポイント解説「1.電圧源と電流源の等価変換」の通り,破線で囲まれた部分を等価変換すると,図5のようになり,図5における電圧\( \ E^{\prime } \ \)と\( \ r \ \)の大きさは,
\[
\begin{eqnarray}
E^{\prime }&=&7\times 3 \\[ 5pt ]
&=&21 \ \mathrm {[V]} \\[ 5pt ]
r&=&3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図2における\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&1+r \\[ 5pt ]
&=&1+3 \\[ 5pt ]
&=&4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
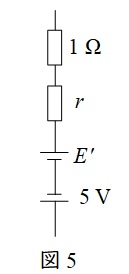
(2)解答:ル
(1)より,図2における\( \ E \ \)は,電源の向きに注意すると,
\[
\begin{eqnarray}
E&=&E^{\prime }-5 \\[ 5pt ]
&=&21-5 \\[ 5pt ]
&=&16 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
ワンポイント解説「2.ミルマンの定理」より,抵抗\( \ R_{1} \ \)の開放電圧\( \ V_{0} \ \)は,
\[
\begin{eqnarray}
V_{0}&=&\frac {\displaystyle \frac {4}{2}+\frac {E}{R}}{\displaystyle \frac {1}{2}+\frac {1}{R}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {4}{2}+\frac {16}{4}}{\displaystyle \frac {1}{2}+\frac {1}{4}} \\[ 5pt ]
&=&\frac {2+4}{\displaystyle \frac {3}{4}} \\[ 5pt ]
&=&8 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であり,抵抗\( \ R_{1} \ \)から電源側を見たときの合成抵抗\( \ R_{0} \ \)は,電圧源を短絡すると,
\[
\begin{eqnarray}
R_{0}&=&\frac {2\times R}{2+R} \\[ 5pt ]
&=&\frac {2\times 4}{2+4} \\[ 5pt ]
&=&\frac {4}{3} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,抵抗\( \ R_{1} \ \)に流れる電流\( \ I_{1} \ \)は,ワンポイント解説「3.テブナンの定理」より,
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{0}}{R_{0}+R_{1}} \\[ 5pt ]
&=&\frac {8}{\displaystyle \frac {4}{3}+R_{1}} \\[ 5pt ]
&=&\frac {8}{\displaystyle \frac {4+3R_{1}}{3}} \\[ 5pt ]
&=&\frac {24}{3R_{1}+4} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ニ
\( \ R_{1} \ \)の消費電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&{I_{1}}^{2}R_{1} \\[ 5pt ]
&=&\left( \frac {24}{3R_{1}+4}\right) ^{2}R_{1} \\[ 5pt ]
&=&\frac {576R_{1}}{9R_{1}^{2}+24R_{1}+16} ・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに整理すると,
\[
\begin{eqnarray}
P&=&\frac {576}{\displaystyle 9R_{1}+24+\frac {16}{R_{1}}}\\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \displaystyle A=9R_{1}+24+\frac {16}{R_{1}} \ \)とおくと,\( \ A \ \)が最小値をとるとき\( \ P \ \)が最大となり,\( \ A \ \)が最小値をとるとき,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R_{1}}=0 \ \)となるので,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R_{1}}=9-\frac {16}{R_{1}^{2}}&=&0\\[ 5pt ]
\frac {16}{R_{1}^{2}}&=&9\\[ 5pt ]
R_{1}^{2}&=&\frac {16}{9} \\[ 5pt ]
R_{1}&=&\frac {4}{3} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
\( \ \displaystyle R_{1}=\frac {4}{3} \ \mathrm {[\Omega ]} \ \)を①式に代入すると,
\[
\begin{eqnarray}
P&=&\frac {576R_{1}}{9R_{1}^{2}+24R_{1}+16} \\[ 5pt ]
&=&\frac {\displaystyle 576\times \frac {4}{3}}{\displaystyle 9\times \left( \frac {4}{3}\right) ^{2}+24\times \frac {4}{3}+16} \\[ 5pt ]
&=&\frac {768}{16+32+16} \\[ 5pt ]
&=&12.0 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは