Contents
【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ 10 \ \mathrm {kV\cdot A} \ \),定格一次電圧\( \ 2 \ 000 \ \mathrm {V} \ \),定格二次電圧\( \ 110 \ \mathrm {V} \ \),定格周波数\( \ 60 \ \mathrm {Hz} \ \)の単相変圧器があり,試験結果は次のとおりであった。
無負荷試験 無負荷損:\( \ P_{0}=200 \ \mathrm {W} \ \)
無負荷電流:\( \ I_{0}=0.26 \ \mathrm {A} \ \)
短絡試験 インピーダンス電圧:\( \ V_{\mathrm {1s}}=100 \ \mathrm {V} \ \)
一次電流:\( \ I_{\mathrm {1s}}=5 \ \mathrm {A} \ \)
インピーダンスワット:\( \ P_{\mathrm {s}}=400 \ \mathrm {W} \ \)
この変圧器について次の問に答えよ。
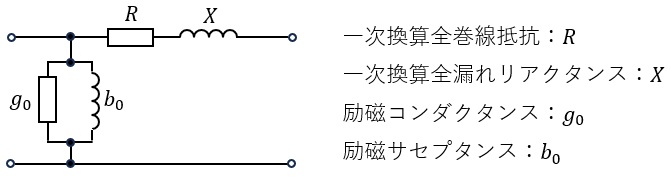
(1) 図に示す一次換算の簡易等価回路の回路定数を求めよ。
(2) 百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)を求めよ。
(3) 遅れ力率\( \ 80 \ \mathrm {%} \ \),全負荷における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)を求めよ。
(4) 遅れ力率\( \ 80 \ \mathrm {%} \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における電圧の変動率\( \ \varepsilon ^{\prime } \ \mathrm {[%]} \ \)を求めよ。
ただし,定格負荷時の力率\( \ \cos \phi \ \)における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,百分率抵抗降下を\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下を\( \ q \ \mathrm {[%]} \ \)とすれば,次式で表せるものとする。
\[
\begin{eqnarray}
\varepsilon &=& p\cos \phi +q\sin \phi \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
変圧器の無負荷試験と短絡試験に関する問題です。
後半の(3)と(4)は難易度は比較的高いですが,平成28年機械制御科目問2に類題が出題されたため,多くの受験生が選択した問題かと思います。
機械制御科目は問題選択も重要なので,過去問の類題を速やかに判断できると大きなアドバンテージになります。
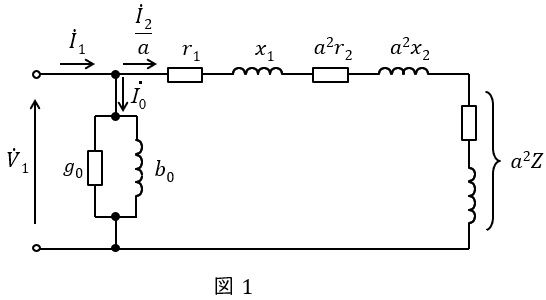
1.変圧器の\( \ \mathrm {L} \ \)形等価回路(一次換算)
変圧器の一次換算等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ a \ \)は変圧比(巻数比)となります。
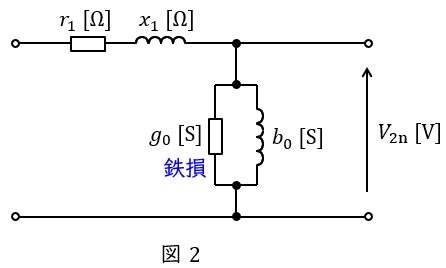
2.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して,二次側に定格電圧を加える試験です。測定される電力は鉄損となり,測定される電力と電流から,励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)及び励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが,二次側開放で一次側に定格電圧を加えても同様に求められます。
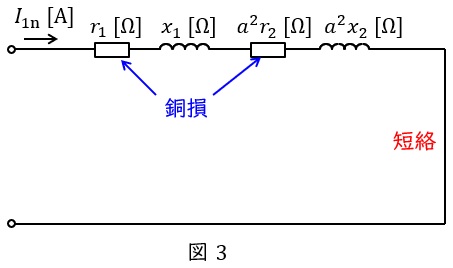
3.短絡試験の等価回路
変圧器の短絡試験は二次側を短絡して,一次側にインピーダンス電圧を加えて,定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると,測定される電力は銅損となります。測定される電力と電流から,高圧側換算の巻線抵抗\( \ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ \)及び漏れリアクタンス\( \ X=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ \)を求めることが可能となります。
4.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス(パーセントインピーダンス)\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
5.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)
変圧器の一次二次を合算した二次側換算の抵抗成分を\( \ R=\displaystyle \frac {r_{1}}{a^{2}}+r_{2} \ \),一次二次を合算した二次側換算のリアクタンス成分を\( \ X=\displaystyle \frac {x_{1}}{a^{2}}+x_{2} \ \)とし,定格二次電圧を\( \ V_{\mathrm {2n}} \ \mathrm {[V]} \ \),定格二次電流を\( \ I_{\mathrm {2n}} \ \mathrm {[A]} \ \)とすると,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
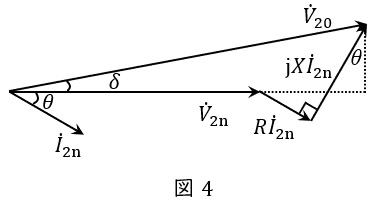
定格負荷(遅れ力率\( \ \cos \theta \ \))を接続したときの変圧器のベクトル図は図4のように描くことができ,電圧変動率\( \ \varepsilon \ \)は上記\( \ p \ \),\( \ q \ \)を用いると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≃&p\cos \theta + q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と近似することができ,\( \ {\dot V}_{\mathrm {20}} \ \)と\( \ {\dot V}_{\mathrm {2n}} \ \)の位相差が十分に小さく,\( \ \varepsilon \ \)が\( \ 4 % \ \)以下の場合には,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta + q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
と近似することができます。
【解答】
(1)一次換算の簡易等価回路の回路定数
ワンポイント解説「2.無負荷試験の等価回路」の通り,無負荷試験時には励磁回路のみに電流が流れると考えれば良い。問題図の等価回路は一次側に定格電圧\( \ V_{\mathrm {1n}}=2 \ 000 \ \mathrm {[V]} \ \)を加えたときの試験回路であるから,励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)は,
\[
\begin{eqnarray}
P_{0} &=& g_{0}V_{\mathrm {1n}}^{2} \\[ 5pt ]
g_{0} &=&\frac {P_{0}}{V_{\mathrm {1n}}^{2}} \\[ 5pt ]
&=&\frac {200}{2 \ 000^{2}} \\[ 5pt ]
&=&5.00 \times 10^{-5} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,励磁アドミタンス\( \ Y_{0} \ \mathrm {[S]} \ \)は,
\[
\begin{eqnarray}
Y_{0} &=&\frac {I_{0}}{V_{\mathrm {1n}}} \\[ 5pt ]
&=&\frac {0.26}{2 \ 000} \\[ 5pt ]
&=&1.3 \times 10^{-4} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)は,
\[
\begin{eqnarray}
b_{0} &=&\sqrt {Y_{0}^{2}-g_{0}^{2}} \\[ 5pt ]
&=&\sqrt {\left( 1.3 \times 10^{-4}\right) ^{2}-\left( 5.00 \times 10^{-5}\right) ^{2}} \\[ 5pt ]
&=&1.2 \times 10^{-4} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
また,ワンポイント解説「3.短絡試験の等価回路」の通り,短絡試験時には励磁回路の電流は十分に小さいと考えれば良いので,短絡試験の結果より一次換算全巻線抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {s}} &=& RI_{\mathrm {1s}}^{2} \\[ 5pt ]
R&=&\frac {P_{\mathrm {s}}}{I_{\mathrm {1s}}^{2}} \\[ 5pt ]
&=&\frac {400}{5^{2}} \\[ 5pt ]
&=&16 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,一次二次の合成したインピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
Z &=&\frac {V_{\mathrm {1s}}}{I_{\mathrm {1s}}} \\[ 5pt ]
&=&\frac {100}{5} \\[ 5pt ]
&=&20 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,一次換算全漏れリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
X &=&\sqrt {Z^{2}-R^{2}} \\[ 5pt ]
&=&\sqrt {20^{2}-16^{2}} \\[ 5pt ]
&=&12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)
定格容量\( \ P_{\mathrm {n}}=10 \ \mathrm {[kV\cdot A]} \ \),一次定格電圧\( \ V_{\mathrm {1n}}=2 \ 000 \ \mathrm {[V]} \ \)より,一次定格電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {1n}}&=&\frac {P_{\mathrm {n}}}{V_{\mathrm {1n}}} \\[ 5pt ]
&=&\frac {10\times 10^{3}}{2 \ 000} \\[ 5pt ]
&=&5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,ワンポイント解説「5.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)」の通り,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ]
&=&\frac {16\times 5}{2 \ 000} \times 100 \\[ 5pt ]
&=&4 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ]
&=&\frac {12\times 5}{2 \ 000} \times 100 \\[ 5pt ]
&=&3 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)遅れ力率\( \ 80 \ \mathrm {%} \ \),全負荷における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)
\( \ \cos \phi =0.8 \ \)より\( \ \sin \phi \ \)は,
\[
\begin{eqnarray}
\sin \phi &=&\sqrt {1-\cos ^{2}\phi } \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となるので,電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,ワンポイント解説「5.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)」の通り,
\[
\begin{eqnarray}
\varepsilon &=& p\cos \phi +q\sin \phi \\[ 5pt ]
&=& 4\times 0.8 +3\times 0.6 \\[ 5pt ]
&=& 5.0 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)遅れ力率\( \ 80 \ \mathrm {%} \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における電圧の変動率\( \ \varepsilon ^{\prime } \ \mathrm {[%]} \ \)
\( \ \displaystyle \frac {1}{2} \ \)負荷の時は負荷電流が\( \ \displaystyle \frac {1}{2} \ \)となるので,比例する百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)が\( \ \displaystyle \frac {1}{2} \ \)となる。したがって,電圧変動率\( \ \varepsilon ^{\prime } \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=& \frac {1}{2}p\cos \phi +\frac {1}{2}q\sin \phi \\[ 5pt ]
&=& \frac {1}{2}\times 4\times 0.8 +\frac {1}{2}\times 3\times 0.6 \\[ 5pt ]
&=& 2.5 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは