【問題】
【難易度】★★☆☆☆(やや易しい)
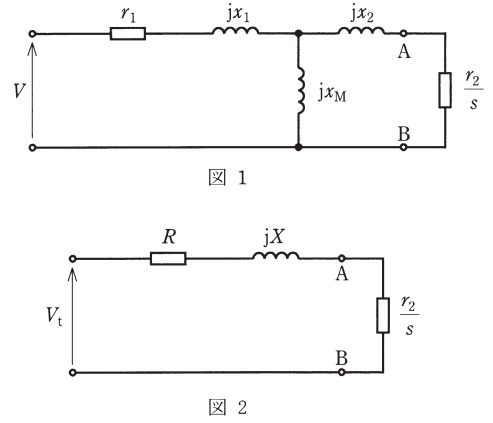
\( \ 400 \ \mathrm {[V]} \ \),\( \ 60 \ \mathrm {[Hz]} \ \),\( \ 4 \ \)極の三相誘導電動機がある。二次側諸量を一次側に換算した星形\( \ 1 \ \)相分の\( \ \mathrm {T} \ \)形等価回路を図1に示す。図中の\( \ s \ \)は滑り,\( \ V \ \)は一次電圧(星形相電圧)であり,また,等価回路定数は次のとおりである。
\( \ r_{1}=0.2 \ \mathrm {[\Omega ]} \ \),\( \ x_{1}=0.5 \ \mathrm {[\Omega ]} \ \),\( \ x_{\mathrm {M}}=20 \ \mathrm {[\Omega ]} \ \)
\( \ r_{2}=0.1 \ \mathrm {[\Omega ]} \ \)(一次側換算値),\( \ x_{2}=0.2 \ \mathrm {[\Omega ]} \ \)(一次側換算値)
次の問に答えよ。
(1) 図1の\( \ \mathrm {T} \ \)形等価回路は鳳・テブナンの定理によると,図2の回路で表される。
a. 電動機に線間電圧\( \ 400 \ \mathrm {[V]} \ \)を印加し,同期速度で回転しているとき,図1の端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)間に現れる電圧\( \ V_{\mathrm {t}} \ \mathrm {[V]} \ \)を求めよ。
b. 図1で一次端子を短絡したとき,端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)から一次側をみた合成インピーダンス\( \ R+\mathrm {j}X \ \mathrm {[\Omega ]} \ \)を求めよ。
(2) 図2の回路から,始動時に二次回路に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)(一次側換算値)及び始動トルク\( \ T_{\mathrm {s}} \ \mathrm {[N\cdot m]} \ \)を求めよ。
【ワンポイント解説】
誘導電動機の問題というよりも,理論科目の鳳・テブナンの定理を知っているかどうかを問うような問題となっています。\( \ 3 \ \)種から非常によく出題される定理と思いますので,計算間違いに注意して完答を目指すようにしましょう。
1.鳳・テブナンの定理
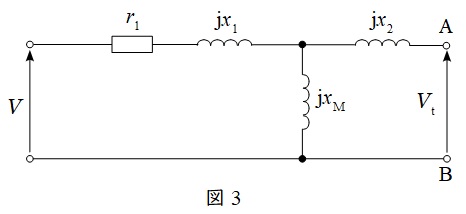
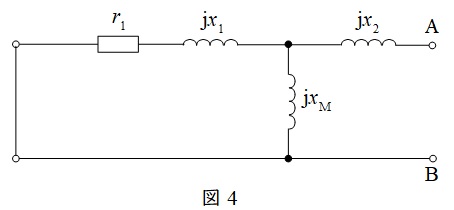
図1において,受電端開放時の\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)間の電位差を\( \ V_{\mathrm {t}} \ \mathrm {[V]} \ \)(図3),電圧源を短絡し,電流源を開放した時の端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)から見た合成インピーダンスをを\( \ R+\mathrm {j}X \ \mathrm {[\Omega ]} \ \)(図4)とした時,図2のような回路に置き換えられるという定理です。
【関連する「電気の神髄」記事】
【解答】
(1)a.図1の端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)間に現れる電圧\( \ V_{\mathrm {t}} \ \mathrm {[V]} \ \)
図3の回路において,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {t}}&=&\left| \frac {\mathrm {j}x_{\mathrm {M}}}{r_{1}+\mathrm {j}x_{1}+\mathrm {j}x_{\mathrm {M}}}\right| \cdot V \\[ 5pt ]
&=&\frac {x_{\mathrm {M}}}{\sqrt { r_{1}^{2}+\left( x_{1}+x_{\mathrm {M}}\right) ^{2}}} \cdot V \\[ 5pt ]
&=&\frac {20}{\sqrt { 0.2^{2}+\left( 0.5+20 \right) ^{2}}}\times \frac {400}{\sqrt {3}} \\[ 5pt ]
&≒&225.30 → 225 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b.図1で一次端子を短絡したとき,端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)から一次側をみた合成インピーダンス\( \ R+\mathrm {j}X \ \mathrm {[\Omega ]} \ \)
図4より,\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)から一次側をみた合成インピーダンス\( \ R+\mathrm {j}X \ \)は,
\[
\begin{eqnarray}
R+\mathrm {j}X&=&\frac {\left( r_{1}+\mathrm {j}x_{1}\right) \cdot \mathrm {j}x_{\mathrm {M}}}{\left( r_{1}+\mathrm {j}x_{1}\right) + \mathrm {j}x_{\mathrm {M}}}+\mathrm {j}x_{2} \\[ 5pt ]
&=&\frac {\left( 0.2+\mathrm {j}0.5\right) \cdot \mathrm {j}20}{\left( 0.2+\mathrm {j}0.5\right) + \mathrm {j}20}+\mathrm {j}0.2 \\[ 5pt ]
&=&\frac {-10+\mathrm {j}4}{0.2+\mathrm {j}20.5}+\mathrm {j}0.2 \\[ 5pt ]
&=&\frac {\left( -10+\mathrm {j}4\right) \left( 0.2-\mathrm {j}20.5\right) }{\left( 0.2+\mathrm {j}20.5\right) \left( 0.2-\mathrm {j}20.5\right) }+\mathrm {j}0.2 \\[ 5pt ]
&=&\frac {80+\mathrm {j}205.8}{0.04+420.25}+\mathrm {j}0.2 \\[ 5pt ]
&≒&0.19034+\mathrm {j}0.48966+\mathrm {j}0.2 \\[ 5pt ]
&≒&0.19034+\mathrm {j}0.68966 → 0.190+\mathrm {j}0.690 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)始動時に二次回路に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)(一次側換算値)及び始動トルク\( \ T_{\mathrm {s}} \ \mathrm {[N\cdot m]} \ \)
始動時の滑り\( \ s \ \)は\( \ 1 \ \)であるから,図2の回路において,二次回路に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2}&=&\left| \frac {V_{\mathrm {t}}}{R+\mathrm {j}X+r_{2}}\right| \\[ 5pt ]
&=&\frac {V_{\mathrm {t}}}{\sqrt {\left( R+r_{2}\right) ^{2}+X^{2}}} \\[ 5pt ]
&=&\frac {225.30}{\sqrt{ \left( 0.19034+0.1\right) ^{2}+0.68966^{2}}} \\[ 5pt ]
&≒&\frac {225.30}{0.74828} \\[ 5pt ]
&≒&301.09 → 301 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,始動トルク\( \ T_{\mathrm {s}} \ \mathrm {[N\cdot m]} \ \)は,二次入力\( \ P_{2} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)を用いると,
\[
\begin{eqnarray}
T_{\mathrm {s}}&=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {3r_{2}I_{2}^{2}}{\displaystyle \frac {4\pi f}{p}} \\[ 5pt ]
&=&\frac {3\times 0.1\times 301.09^{2}}{\displaystyle \frac {4\pi \times 60}{4}} \\[ 5pt ]
&≒&144.28 → 144 \ \mathrm {[N\cdot m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは