《機械・制御》〈パワーエレクトロニクス〉[R06:問3]降圧チョッパの動作と各電圧電流に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

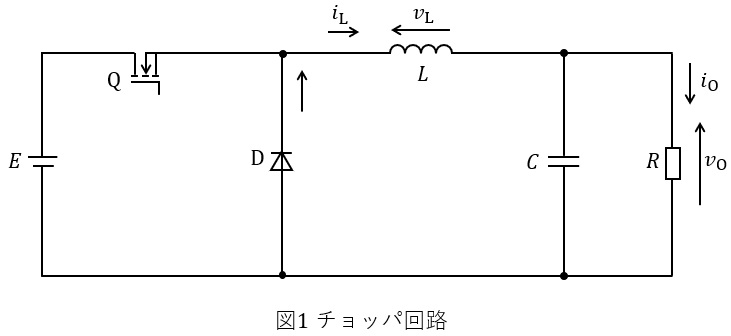
図1は電源電圧を\( \ E \ \)，負荷電圧を\( \ v_{\mathrm {O}} \ \)とし，抵抗成分を無視できるインダクタンス\( \ L \ \)とキャパシタンス\( \ C \ \)によるチョッパ回路である。理想的な半導体スイッチ\( \ \mathrm {Q} \ \)と順方向電圧降下を無視できるダイオード\( \ \mathrm {D} \ \)を用いている。\( \ E= 12 \ \mathrm {V} \ \)，\( \ L=450 \ \mathrm {\mu H} \ \)，\( \ R=1 \ \mathrm {\Omega } \ \)であり，十分に大きい\( \ C \ \)によって\( \ v_{\mathrm {O}} \ \)は一定値\( \ V_{\mathrm {O}} \ \)，負荷電流\( \ i_{\mathrm {O}} \ \)は一定値\( \ I_{\mathrm {O}} \ \)とみなすことができる。\( \ \mathrm {Q} \ \)は図2のオン・オフ状態で動作しており，この回路は周期定常状態にあるものとする。図2と同じものが答案用紙に描かれている。インダクタ電流は連続しているものとして，以下の問に答えよ。

(1)　インダクタ電圧\( \ v_{\mathrm {L}} \ \)の波形を答案用紙に描け。なお，\( \ v_{\mathrm {L}} \ \)の最大値及び最小値を図中に\( \ E \ \)と\( \ v_{\mathrm {O}}=\left( V_{\mathrm {O}}\right) \ \)を用いて表せ。

(2)　\( \ V_{\mathrm {O}} \ \)の値を求めよ。

(3)　\( \ I_{\mathrm {O}} \ \)の値を求めよ。

(4)　インダクタ電流\( \ i_{\mathrm {L}} \ \)の平均値\( \ I_{\mathrm {L}} \ \)を求めよ。

(5)　\( \ i_{\mathrm {L}} \ \)の最大値と最小値の差（リプル）を求めよ。

(6)　\( \ i_{\mathrm {L}} \ \)の波形を答案用紙に描け。最大値と最小値を明示せよ。

(7)　ダイオード電流\( \ i_{\mathrm {D}} \ \)の波形を答案用紙に描け。最大値を明示せよ。

(8)　\( \ i_{\mathrm {L}} \ \)の最大値と最小値の差（リプル）を\( \ 0.1 \ \mathrm {A} \ \)とするための\( \ L \ \)の値を求めよ。

【ワンポイント解説】

直流チョッパのうち，降圧チョッパの動作と電圧電流を検討する問題です。
パワーエレクトロニクスの問題としてはかなり取り組みやすい問題で，(5)の考え方を理解していれば完答を目指せるかと思います。
近年はパワーエレクトロニクスの問題も解きやすい問題が増えている印象ですので，最初から捨てるのではなく勉強範囲に入れていくようにして下さい。

1.降圧チョッパの動作
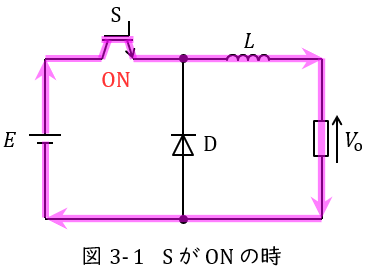
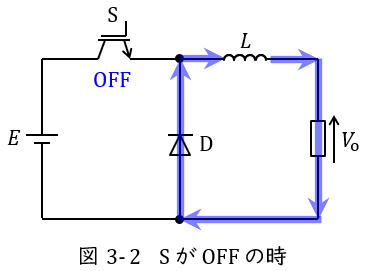
図3-1及び図3-2は降圧チョッパの例となります。
スイッチ\( \ \mathrm {S} \ \)がオンになると，図3-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側に電流が流れますが，ダイオード\( \ D_{\mathrm {F}} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図3-2のように電源から電流は流れず，リアクトルに蓄えられているエネルギーから出力側と還流ダイオード\( \ D_{\mathrm {F}} \ \)に電流が流れます。
したがって，降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {out}} \ \)は，スイッチのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，\( \ V_{\mathrm {in}} \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

【解答】

(1)インダクタ電圧\( \ v_{\mathrm {L}} \ \)の波形
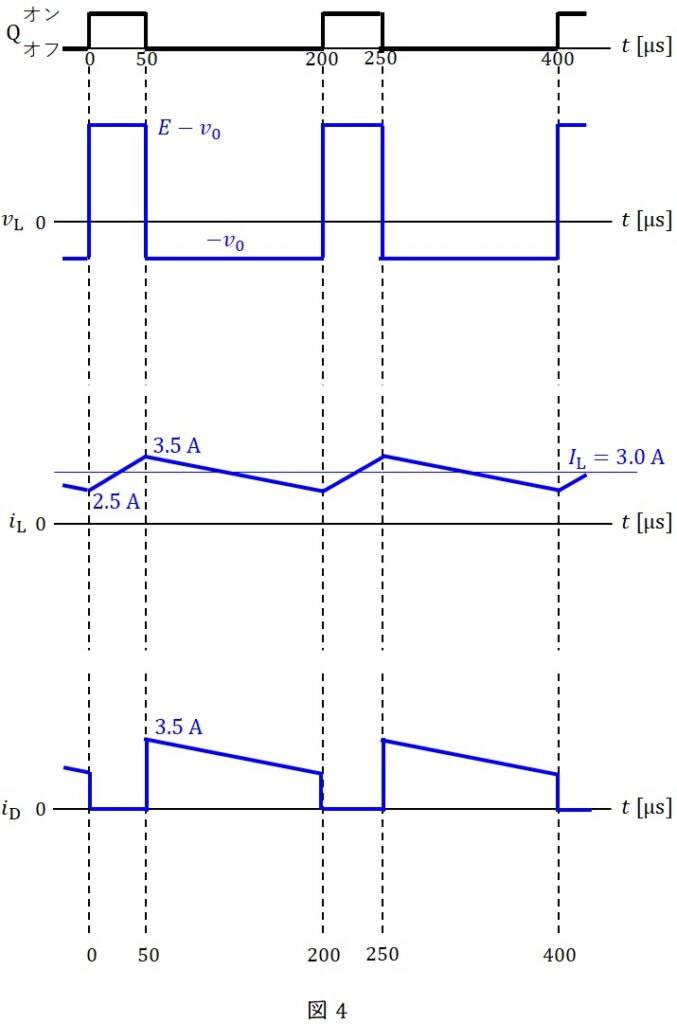
ワンポイント解説「1.降圧チョッパの動作」の通り，スイッチ\( \ \mathrm {Q} \ \)がオンのときはインダクタンス\( \ L \ \)には\( \ E-v_{\mathrm {O}} \ \)，スイッチ\( \ \mathrm {Q} \ \)がオフのときはインダクタンス\( \ L \ \)には\( \ -v_{\mathrm {O}} \ \)の電圧が加わるため，波形は図4の通りとなる。

(2)\( \ V_{\mathrm {O}} \ \)の値
図2より，\( \ T_{\mathrm {ON}}=50 \ \mathrm {[\mu s]} \ \)及び\( \ T_{\mathrm {OFF}}=150 \ \mathrm {[\mu s]} \ \)であるので，負荷電圧\( \ V_{\mathrm {O}} \ \mathrm {[V]} \ \)は，ワンポイント解説「1.降圧チョッパの動作」の通り，
\[
\begin{eqnarray}
V_{\mathrm {O}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] &=&\frac {50}{50+150}\times 12 \\[ 5pt ] &=&3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)\( \ I_{\mathrm {O}} \ \)の値
(2)より，負荷電流\( \ I_{\mathrm {O}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {O}}&=&\frac {V_{\mathrm {O}}}{R} \\[ 5pt ] &=&\frac {3}{1} \\[ 5pt ] &=&3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)インダクタ電流\( \ i_{\mathrm {L}} \ \)の平均値\( \ I_{\mathrm {L}} \ \)
キャパシタンス\( \ C \ \)にはオンのときに電荷が蓄えられ，オフのときに電荷が放出され，定常状態においてはその電流の平均値\( \ I_{\mathrm {C}} \ \)は零となる。したがって，インダクタ電流\( \ i_{\mathrm {L}} \ \)の平均値\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&I_{\mathrm {O}}+I_{\mathrm {C}} \\[ 5pt ] &=&3+0 \\[ 5pt ] &=&3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)\( \ i_{\mathrm {L}} \ \)の最大値と最小値の差（リプル）
インダクタの電圧は\( \ \displaystyle v_{\mathrm {L}}=L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t} \ \)であり，これを変形すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {v_{\mathrm {L}}}{L} \\[ 5pt ] \end{eqnarray}
\] となる。オンのときを考えると，\( \ v_{\mathrm {L}}=E-V_{\mathrm {O}}=12-3=9 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {9}{450\times 10^{-6}} \\[ 5pt ] &=&20 \ 000 \ \mathrm {[A / s]} \\[ 5pt ] \end{eqnarray}
\] となり，オンの期間\( \ T_{\mathrm {ON}}=50 \ \mathrm {[\mu s]} \ \)での変化量\( \ \Delta i_{\mathrm {L}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
\Delta i_{\mathrm {L}}&=&\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}T_{\mathrm {ON}} \\[ 5pt ] &=&20 \ 000 \times 50 \times 10^{-6} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)\( \ i_{\mathrm {L}} \ \)の波形
(4)及び(5)より，\( \ i_{\mathrm {L}} \ \)の最大値\( \ I_{\mathrm {Lmax}} \ \mathrm {[A]} \ \)及び\( \ I_{\mathrm {Lmin}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {Lmax}}&=&I_{\mathrm {L}}+\frac {\Delta i_{\mathrm {L}}}{2} \\[ 5pt ] &=&3+\frac {1}{2} \\[ 5pt ] &=&3.5 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {Lmin}}&=&I_{\mathrm {L}}-\frac {\Delta i_{\mathrm {L}}}{2} \\[ 5pt ] &=&3-\frac {1}{2} \\[ 5pt ] &=&2.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，波形は図4の通りとなる。

(7)ダイオード電流\( \ i_{\mathrm {D}} \ \)の波形
ワンポイント解説「1.降圧チョッパの動作」の通り，ダイオード\( \ \mathrm {D} \ \)にはスイッチ\( \ \mathrm {Q} \ \)がオフのときに流れるため，波形は図4の通りとなる。

(8)\( \ i_{\mathrm {L}} \ \)の最大値と最小値の差（リプル）を\( \ 0.1 \ \mathrm {A} \ \)とするための\( \ L \ \)の値
(5)と同様に考えると，
\[
\begin{eqnarray}
v_{\mathrm {L}}&=&L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t} \\[ 5pt ] L&=&v_{\mathrm {L}}\frac {\mathrm {d}t}{\mathrm {d}i_{\mathrm {L}}} \\[ 5pt ] &=&9\times \frac {50 \times 10^{-6}}{0.1} \\[ 5pt ] &=&4.5 \times 10^{-3} \ \mathrm {[H]}　→　4.5 \ \mathrm {[mH]} \\[ 5pt ] \end{eqnarray}
\] と求められる。