Contents
【問題】
【難易度】★★★☆☆(普通)
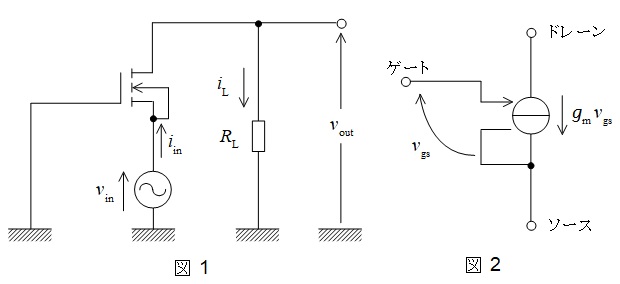
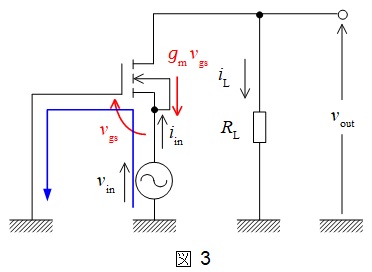
次の文章は,図1に示す\(\mathrm {MOSFET}\)を用いた増幅回路に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選びなさい。ただし,図1は増幅回路の交流成分のみを考慮しており,\(\mathrm {MOSFET}\)の交流等価回路は図2で表されるものとする。また,抵抗\(R_{\mathrm {L}}\)を\(25 \ \mathrm {k\Omega }\),伝達コンダクタンス\(g_{\mathrm {m}}\)を\(1.0 \ \mathrm {mS }\)とする。
図2の\(\mathrm {MOSFET}\)の交流等価回路を使って得られる図1の増幅回路の交流等価回路において,\(v_{\mathrm {gs}}\)は\(v_{\mathrm {gs}}=\fbox { (1) }\)であるので,電流\(i_{\mathrm {in}}\)は\(i_{\mathrm {in}}=\fbox { (2) }\)となる。この結果に数値を代入すると,図1の増幅回路の入力抵抗が\(\displaystyle \frac {v_{\mathrm {in}}}{i_{\mathrm {in}}}=\fbox { (3) } \ \mathrm {k\Omega }\)であることが分かる。さらに,\(i_{\mathrm {L}}\)は\(i_{\mathrm {in}}\)に等しいので,\(v_{\mathrm {out}}\)を\(R_{\mathrm {L}}\),\(g_{\mathrm {m}}\),\(v_{\mathrm {in}}\)を用いて表すと,\(v_{\mathrm {out}}=\fbox { (4) }\)であることが分かる。この結果に数値を代入すると,増幅度\(\displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}\)は\(\displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}=\fbox { (5) }\)倍となる。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& 1.0 &(ロ)& -v_{\mathrm {in}} &(ハ)& -g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {in}} \\[ 5pt ]
&(ニ)& -g_{\mathrm {m}}v_{\mathrm {in}} &(ホ)& g_{\mathrm {m}}v_{\mathrm {in}} &(ヘ)& g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {in}} \\[ 5pt ]
&(ト)& 2v_{\mathrm {in}} &(チ)& 5.0 &(リ)& v_{\mathrm {in}} \\[ 5pt ]
&(ヌ)& \frac {g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {in}}}{2} &(ル)& \frac {g_{\mathrm {m}}v_{\mathrm {in}}}{2} &(ヲ)& -25 \\[ 5pt ]
&(ワ)& 2.0 &(カ)& 25 &(ヨ)& -1.0
\end{eqnarray}
\]
【ワンポイント解説】
\(\mathrm {MOSFET}\)からの出題ですが,バイポーラトランジスタと計算方法は変わりません。計算はそれほど難しくありませんが,プラスとマイナスの符号を間違えてしまうとすべて誤答となってしまう可能性があります。注意して解くようにして下さい。
【解答】
(1)解答:ロ
図3の青色閉路部についてキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
v_{\mathrm {in}}+v_{\mathrm {gs}} &=& 0 \\[ 5pt ]
v_{\mathrm {gs}}&=&-v_{\mathrm {in}}
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
\(\mathrm {MOSFET}\)において,ゲート電流は十分に小さく,ソース電流とドレーン電流はほぼ等しいので,
\[
\begin{eqnarray}
i_{\mathrm {in}} &=& -g_{\mathrm {m}}v_{\mathrm {gs}} \\[ 5pt ]
&=&g_{\mathrm {m}}v_{\mathrm {in}}
\end{eqnarray}
\]
と求められる。
(3)解答:イ
(1),(2)より,
\[
\begin{eqnarray}
\frac {v_{\mathrm {in}}}{i_{\mathrm {in}}} &=& \frac {v_{\mathrm {in}}}{g_{\mathrm {m}}v_{\mathrm {in}}} \\[ 5pt ]
&=&\frac {1}{g_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {1}{1.0\times 10^{-3}} \\[ 5pt ]
&=&1.0\times 10^{3} \ [\Omega ] → 1.0 \ [\mathrm {k\Omega} ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
\(R_{\mathrm {L}}\)の電圧降下と\(v_{\mathrm {out}}\)が等しいので,
\[
\begin{eqnarray}
v_{\mathrm {out}} &=& R_{\mathrm {L}}i_{\mathrm {L}} \\[ 5pt ]
&=&R_{\mathrm {L}}i_{\mathrm {in}} \\[ 5pt ]
&=&g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(4)より,
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=& g_{\mathrm {m}}R_{\mathrm {L}} \\[ 5pt ]
&=&1.0\times 10^{-3}\times 25\times 10^{3} \\[ 5pt ]
&=&25 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは