Contents
【問題】
【難易度】★★★★☆(やや難しい)
図1は,三相交流電源から単相交流を出力するサイクロコンバータである。このサイクロコンバータに関する次の問に答えよ。ただし,交流電源のインピーダンス,及びコンバータでの電圧降下は無視する。また,負荷は誘導性である。
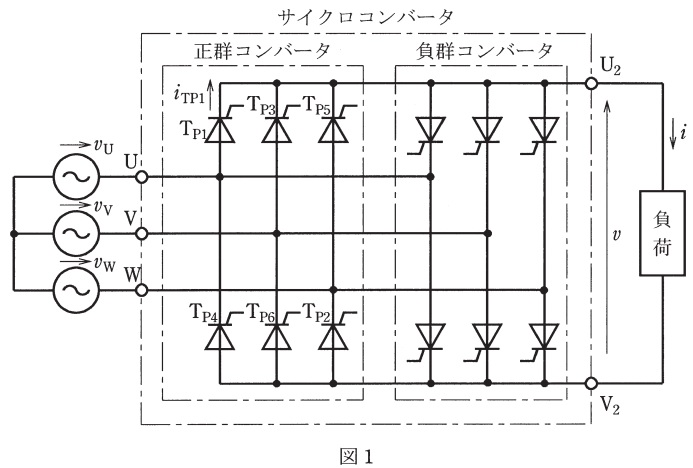
(1) (a)このサイクロコンバータの実用的な出力周波数の上限は電源周波数に対して何分の1程度であるか,また,(b)どのような要因で上限が決まるかを全体で100字程度で説明せよ。
(2) 正群コンバータが,入力交流線間電圧実効値\(E\)及び制御遅れ角\(\alpha \)が一定で,連続した出力電流\(i\)で定常的に動作しているときの出力電圧\(v\)の平均値(直流電圧)\(V_{\mathrm {d}}\)を求める式を示せ。
(3) サイクロコンバータから交流電圧を出力するには,制御遅れ角を時間関数\(\alpha (t)\)として変化させる必要がある。出力電圧\(v\)の基本波電圧\(v_{1}\)を
\[
v_{1}(t)=\sqrt {2} \times 0.8E\sin (2\pi f_{1}t)
\]
とするには,正群コンバータに対しては,\(\alpha (t)\)をどのように与えればよいかを数式で示せ。ここで,出力周波数\(f_{1}\)は電源周波数に比べて十分に低い値とする。また,電流の正負切換時の動作は考慮しない。
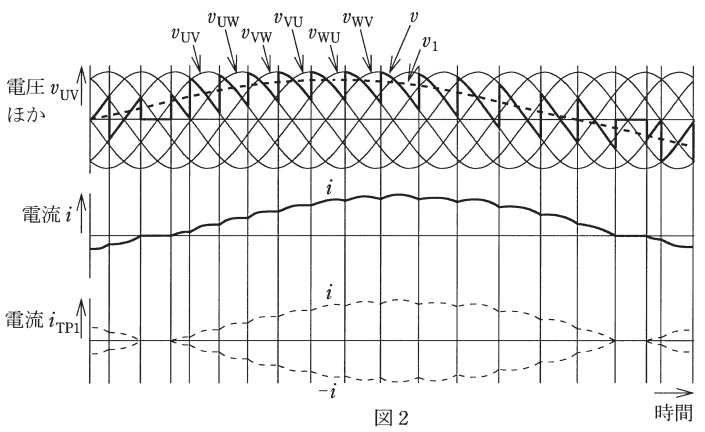
(4) 正群コンバータは,サイリスタが\(\mathrm {T}_{\mathrm {P1}}\),\(\mathrm {T}_{\mathrm {P2}}\), ・・・, \(\mathrm {T}_{\mathrm {P6}}\),\(\mathrm {T}_{\mathrm {P1}}\), ・・・と順番にオンされて動作する。\(\mathrm {T}_{\mathrm {P1}}\)がオンした直後に出力される電圧は,図2に示す\(v_{\mathrm {UV}}\),\(v_{\mathrm {UW}}\),\(v_{\mathrm {VW}}\),\(v_{\mathrm {VU}}\),\(v_{\mathrm {WU}}\),\(v_{\mathrm {WV}}\)の6種類の交流線間電圧のうち,どの電圧となるか。なお,交流線間電圧の記号は,例えば\(v_{\mathrm {UV}}\)は三相交流電源の\(\mathrm {V}\)相を基準とした\(\mathrm {U}\)相の電圧\(v_{\mathrm {UV}}=v_{\mathrm {U}}-v_{\mathrm {V}}\)を表す。また,\(v\)は出力電圧,\(v_{1}\)はその基本波電圧である。
(5) サイクロコンバータの出力には図2に示す電流\(i\)が流れているものとする。図2が答案用紙に印刷されているので,このときに正群コンバータのサイリスタ\(\mathrm {T}_{\mathrm {P1}}\)に流れる電流\(i_{\mathrm {TP1}}\)の波形を太い線で明確に描け。
【ワンポイント解説】
二種の問題としてはかなり難しい問題で,そのまま一種で出題されてもおかしくありません。余程得意なのであれば選択しても良いと思いますが,そうでない場合は他の問題を選択した方が良いと思います。
1.平均値の定義
\(f( \theta )\)を周期\(T \)の周期関数であるとしたとき,平均値\(F_{\mathrm {av}}\)は以下の通りとなります。
\[
F_{\mathrm {av}}=\frac {1}{T}\int _{0}^{T }f( \theta ) \mathrm {d}\theta
\]
【解答】
(1)実用的な出力周波数の上限は電源周波数に対して何分の1程度であるか,またその要因
(ポイント)
・サイクロコンバータでは素子の切換時に短絡を防ぐため,切換時に時限を持たせ,電流を零とするようにしている。
・実用的には\(\displaystyle \frac {1}{2}~\frac {1}{3}\)程度が上限となる。
(試験センター解答例)
(a) 実用的な出力周波数の上限は,電源周波数の\(\displaystyle \frac {1}{2}~\frac {1}{3}\)程度である。(b)出力交流電流の方向が切り換わるときに電源を短絡しないように電流を零としておく期間が必要である。このため,出力周波数が高くなると波形のひずみが大きくなるので出力周波数に上限がある。
(2)出力電圧\(v\)の平均値(直流電圧)\(V_{\mathrm {d}}\)
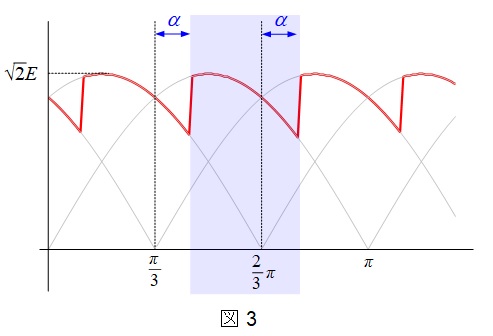
正群コンバータの定常時の出力電圧\(v\)の波形は図3の通りとなる。ここで,最も求めやすい図3の青範囲について平均値\(V_{\mathrm {d}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {1}{\frac {\pi }{3}}\int _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha}\sqrt {2}E\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \int _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \left[ -\cos \theta \right] _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \left[ -\cos \left( \frac {2}{3}\pi+\alpha \right) + \cos \left( \frac {\pi}{3}+\alpha \right) \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \left[ -\cos \frac {2}{3}\pi \cos \alpha + \sin \frac {2}{3}\pi \sin \alpha + \cos \frac {\pi}{3} \cos \alpha – \sin \frac {\pi}{3} \sin \alpha \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \left[ \frac {1}{2}\cos \alpha +\frac {\sqrt {3}}{2} \sin \alpha + \frac {1}{2} \cos \alpha – \frac {\sqrt {3}}{2} \sin \alpha \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}E \cos \alpha
\end{eqnarray}
\]
と求められる。
(3)\(\alpha (t)\)をどのように与えればよいか
出力周波数は,電源周波数よりも十分に低いので,\(v_{1}(t)=v(\alpha )\)とすれば良いから,
\[
\begin{eqnarray}
\sqrt {2} \times 0.8E\sin (2\pi f_{1}t) &=&\frac {3\sqrt {2}}{\pi}E \cos \alpha (t) \\[ 5pt ]
\cos \alpha (t)&=&\frac {\pi \times \sqrt {2} \times 0.8E\sin (2\pi f_{1}t) }{3\sqrt {2}E} \\[ 5pt ]
&=& \frac {0.8\pi }{3}\sin (2\pi f_{1}t) \\[ 5pt ]
\alpha (t)&=&\cos ^{-1}\left( \frac {0.8\pi }{3}\sin (2\pi f_{1}t) \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\(T_{\mathrm {P1}}\)がオンした直後に出力される電圧
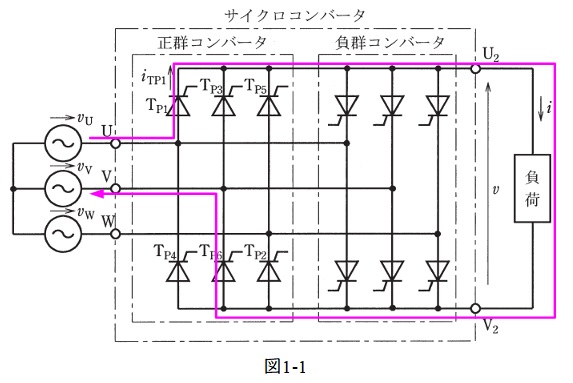
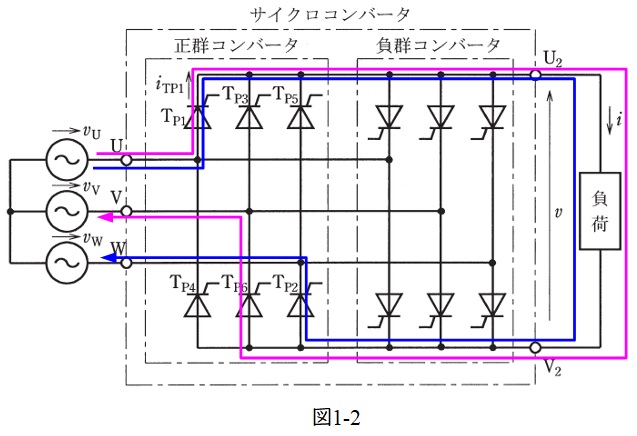
題意より,\(\mathrm {T}_{\mathrm {P1}}\),\(\mathrm {T}_{\mathrm {P2}}\), ・・・, \(\mathrm {T}_{\mathrm {P6}}\),\(\mathrm {T}_{\mathrm {P1}}\), ・・・と順番にONされるので,\(\mathrm {T}_{\mathrm {P1}}\)がONした直後は\(\mathrm {T}_{\mathrm {P1}}\)と\(\mathrm {T}_{\mathrm {P6}}\)がONしている状態となる。したがって,電流は図1-1のように流れ,\(v_{\mathrm {UV}}\)が出力される。
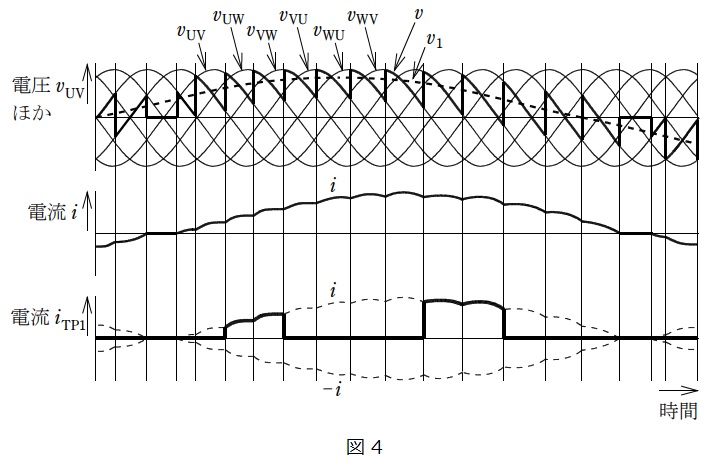
(5)正群コンバータのサイリスタ\(\mathrm {T}_{\mathrm {P1}}\)に流れる電流\(i_{\mathrm {TP1}}\)の波形
\(\mathrm {T}_{\mathrm {P1}}\)がONの時のみ電流が流れるが,\(\mathrm {T}_{\mathrm {P1}}\)がONとなる時は,\(\mathrm {T}_{\mathrm {P6}}\),\(\mathrm {T}_{\mathrm {P1}}\)がON,\(\mathrm {T}_{\mathrm {P1}}\),\(\mathrm {T}_{\mathrm {P2}}\)がONの時となる。したがって,この時に流れる電流は図1-2の時のみとなるので,\(v_{\mathrm {UV}}\)と\(v_{\mathrm {UW}}\)が出力されている時のみ電流が流れる。したがって,図で示すと図4のようになる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは