《機械・制御》〈パワーエレクトロニクス〉[H25:問3]単相交流電力調整回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

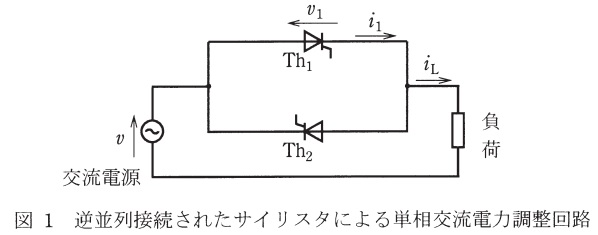
図1は，逆並列接続されたサイリスタによる単相交流電力調整回路を示す。交流電源の電圧を\( \ v=\sqrt {2}V\sin \omega t \ \mathrm {[V]} \ \)，サイリスタ\( \ \mathrm {Th_{1}} \ \)，\( \ \mathrm {Th_{2}} \ \)の制御遅れ角を\( \ \alpha \ \mathrm {[rad]} \ \)として，次の問に答えよ。ただし，サイリスタの損失は無視できるものとする。

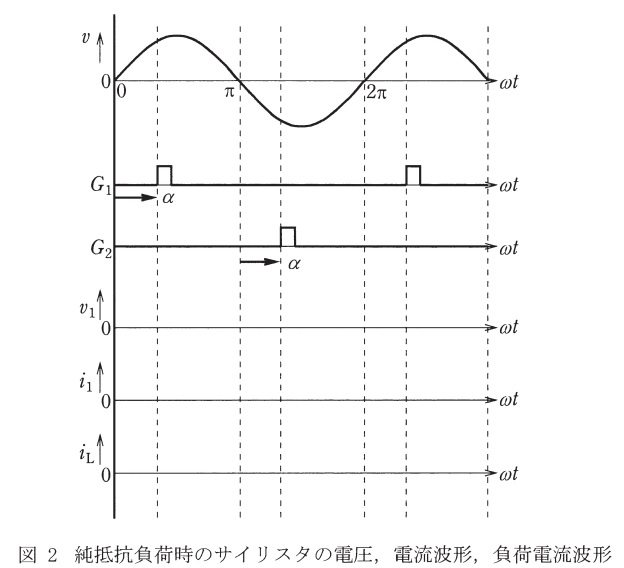
(1)　横軸を\( \ \omega t \ \mathrm {[rad]} \ \)とし，電圧\( \ v \ \)，及び\( \ \mathrm {Th_{1}} \ \)，\( \ \mathrm {Th_{2}} \ \)に加えられるゲートパルス\( \ G_{1} \ \)，\( \ G_{2} \ \)の波形を示した図2と同じ図が答案用紙に印刷されている。これに，負荷が純抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の場合の\( \ \mathrm {Th_{1}} \ \)に加わる電圧\( \ v_{1} \ \)及び流れる電流\( \ i_{1} \ \)の波形，並びに負荷電流\( \ i_{\mathrm {L}} \ \)の波形を太線で明確に示せ。

(2)　(1)における負荷電流\( \ i_{\mathrm {L}} \ \)の実効値\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)を\( \ V \ \)，\( \ R \ \)及び\( \ \alpha \ \)を用いて表せ。
ただし，次式を利用してよい。
\[
\begin{eqnarray}
\int \sin ^{2}\theta \mathrm {d}\theta &=&-\frac {1}{4}\sin 2\theta +\frac {1}{2}\theta +C \\[ 5pt ] \end{eqnarray}
\]

(3)　負荷が純インダクタンスのリアクトルの場合，リアクトルに印加する電圧の制御が可能な制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)の範囲を示せ。

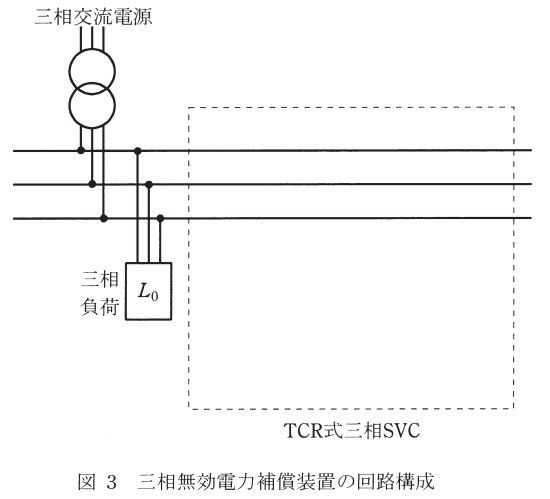
(4)　逆並列接続されたサイリスタによる交流電力調整回路の応用例として，三相無効電力補償装置(\( \ \mathrm {TCR} \ \)式三相\( \ \mathrm {SVC} \ \))がある。この装置は，図3のように三相交流電源に接続された三相負荷\( \ L_{0} \ \)と並列に設け，固定の進み電流と可変の遅れ電流との合計電流によって無効電力を調整する回路構成である。図3と同じ図が答案用紙に印刷されている。これに\( \ \mathrm {TCR} \ \)式三相\( \ \mathrm {SVC} \ \)を構成するコンデンサ，リアクトル及びサイリスタの接続図を示せ。

【ワンポイント解説】

例年のパワーエレクトロニクスに比べると回路は易しいですが，三相無効電力補償装置(\( \ \mathrm {TCR} \ \)式三相\( \ \mathrm {SVC} \ \))の回路を記載するといった難問も含まれています。(3)までは比較的取り組みやすい問題となりますので，解けるようにしておくと良いと思います。

1.サイリスタ
アノード―カソード間に順電圧をかけた状態で，ゲートにパルス電流を流すとターンオンする素子です。
一旦順方向に電流が流れるとゲート信号がなくなってもオン状態を維持します。
順方向の電流を保持電流以下にする，もしくは逆方向に電圧をかけるとサイリスタをオフにすることができます。

2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ 2 \pi \ \)の周期関数であるとしたとき，平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{2\pi }\int _{0}^{2\pi }f( \theta ) d\theta \\[ 5pt ] \end{eqnarray}
\] ②実効値\( \ F \ \)　
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} f( \theta ) ^{2} d\theta } \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)負荷が純抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の場合の\( \ \mathrm {Th_{1}} \ \)に加わる電圧\( \ v_{1} \ \)及び流れる電流\( \ i_{1} \ \)の波形，並びに負荷電流\( \ i_{\mathrm {L}} \ \)の波形
ワンポイント解説「1.サイリスタ」の通り，パルス電流が入った\( \ \omega t=\alpha \ \)の時に順方向電圧がかかっている\( \ \mathrm {Th_{1}} \ \)がオンとなり，その後逆方向電圧がかかる\( \ \omega t=\pi \ \)にて\( \ \mathrm {Th_{1}} \ \)がオフとなります。
その後，\( \ \omega t=\pi +\alpha \ \)の時に順方向電圧がかかっている\( \ \mathrm {Th_{2}} \ \)がオンとなり，その後逆方向電圧がかかる\( \ \omega t=2\pi \ \)にて\( \ \mathrm {Th_{2}} \ \)がオフとなります。
また，\( \ i_{\mathrm {L}} \ \)は\( \ i_{1} \ \)と\( \ \mathrm {Th_{2}} \ \)がオンとなり，流れる電流の合計となります。
\( \ v_{1} \ \)はサイリスタがオフの時のみかかり，サイリスタが導通すると電圧差はなくなります。
以上の条件を図に示すと，図2-2の通りとなります。

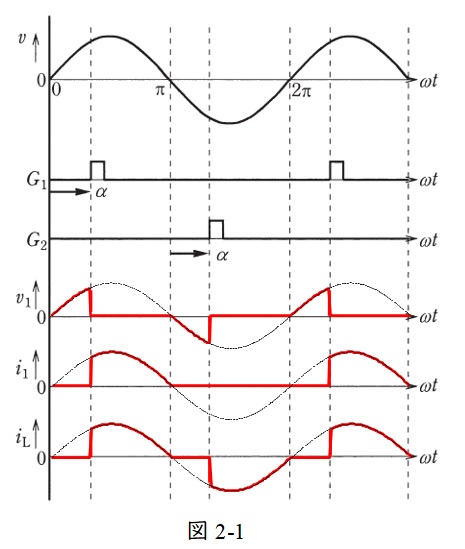
(2)負荷電流\( \ i_{\mathrm {L}} \ \)の実効値\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)
\( \ 0 ＜ \omega t　＜ \alpha \ \)の時，負荷電流\( \ i_{\mathrm {L}}=0 \ \)，\( \ \alpha ＜ \omega t　＜ \pi \ \)の時，負荷電流\( \ i_{\mathrm {L}} \ \)は，
\[
\begin{eqnarray}
i_{\mathrm {L}}&=&\frac {v}{R} \\[ 5pt ] &=&\sqrt {2}\frac {V}{R}\sin \omega t \\[ 5pt ] \end{eqnarray}
\] となる。したがって，その実効値\( \ I_{\mathrm {L}} \ \)は，ワンポイント解説「2.平均値と実効値の定義」の通り，
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&\sqrt {\frac {1}{\pi} \int _{0}^{\pi} i_{\mathrm {L}} ^{2} d\omega t } \\[ 5pt ] &=&\sqrt {\frac {1}{\pi} \int _{\alpha }^{\pi} i_{\mathrm {L}} ^{2} d\omega t } \\[ 5pt ] &=&\sqrt {\frac {2}{\pi }}\frac {V}{R}\sqrt {\int _{\alpha }^{\pi} \sin ^{2}\omega t d\omega t } \\[ 5pt ] &=&\sqrt {\frac {2}{\pi }}\frac {V}{R}\sqrt {\left[ -\frac {1}{4}\sin 2\omega t +\frac {1}{2}\omega t \right] _{\alpha }^{\pi} } \\[ 5pt ] &=&\sqrt {\frac {2}{\pi }}\frac {V}{R}\sqrt {\left[ 0 +\frac {1}{2}\pi +\frac {1}{4}\sin 2\alpha -\frac {1}{2}\alpha \right] } \\[ 5pt ] &=&\frac {V}{\sqrt {\pi }R}\sqrt {\pi -\alpha +\frac {1}{2}\sin 2\alpha } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)負荷が純インダクタンスのリアクトルの場合，リアクトルに印加する電圧の制御が可能な制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)
負荷が純インダクタンスのリアクトルの場合，電流は電圧より\( \ \displaystyle \frac {\pi}{2} \ \)だけ遅れる。点弧角が\( \ \displaystyle \frac {\pi}{2} \ \)になると，電流は正弦波形となり，これ以上に点弧角が大きくなれば制御できることになる。したがって，電圧制御が可能となるのは，\( \ \displaystyle \frac {\pi}{2} ＜ \alpha ＜ \pi \ \)となる。

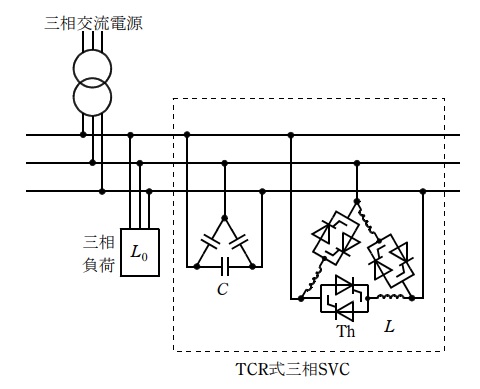
(4)\( \ \mathrm {TCR} \ \)式三相\( \ \mathrm {SVC} \ \)を構成するコンデンサ，リアクトル及びサイリスタの接続図
\( \ \mathrm {TCR} \ \)式三相\( \ \mathrm {SVC} \ \)を構成する回路は下図の通りとなります。ただし，回路は\( \ \Delta \ \)結線となっていますが，\( \ \mathrm {Y} \ \)結線でも大丈夫です。