【問題】
【難易度】★★★★☆(やや難しい)
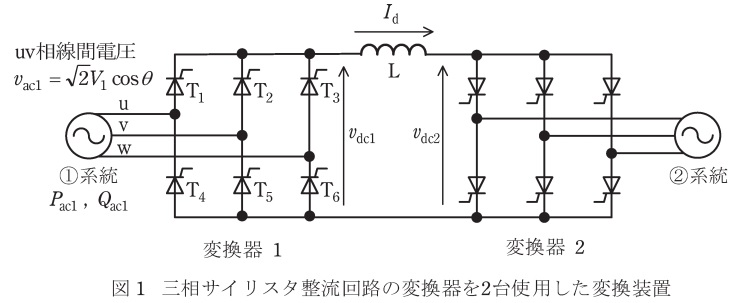
図1に三相サイリスタ変換器を\(2\)台使用した変換装置を示す。対称三相電圧の①系統,②系統に接続されている変換器をそれぞれ変換器\(1\),変換器\(2\)とし,その直流電圧を\( \ v_{\mathrm {dc1}}\),\(v_{\mathrm {dc2}} \ \)とする。①系統の相順は\( \ \mathrm {u→v→w} \ \)相とし,変換器\(1\)のサイリスタの番号を図1に示す。直流リアクトル\( \ \mathrm {L} \ \)のインダクタンスは十分に大きく,直流電流\( \ I_{\mathrm {d}} \ \)のリプルは無視できる。また,図示されていない回路内のインピーダンス及び回路内の損失も無視できるものとする。なお,\(I_{\mathrm {d}}\),\(v_{\mathrm {dc1}}\),\(v_{\mathrm {dc2}}\)の極性は,図1に示す方向を正とする。動作は定常状態にあるものとして,次の問に答えよ。
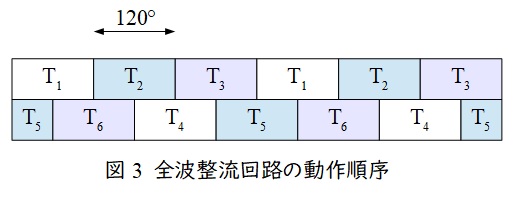
(1) ある時刻に変換器\(1\)のサイリスタ\( \ \mathrm {T}_{1} \ \)及び\( \ \mathrm {T}_{5} \ \)がオンしていたとする。電気角で\( \ 120° \ \)に相当する時間後に通電しているのはどのサイリスタであるかを示せ。
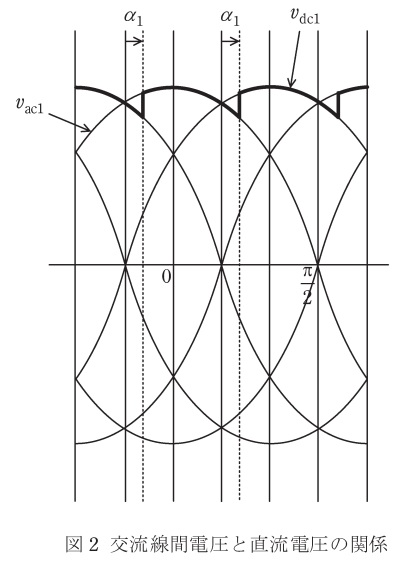
(2) ①系統の三相交流線間電圧の実効値を\( \ V_{1} \ \)とする。変換器\(1\)を図2に示す制御角\( \ \alpha _{1} \ \)で運転したときに,直流電圧\( \ v_{\mathrm {dc1}} \ \)の平均値\( \ V_{\mathrm {dc1}}\)を求める式を,\(V_{1} \ \)及び\( \ \alpha _{1} \ \)を用いて示せ。
(3) 損失がないとしているので,この装置における①系統から入力される有効電力\( \ P_{\mathrm {ac1}} \ \)と直流電力\( \ P_{\mathrm {dc}} \ \)とは等しい。有効電力\( \ P_{\mathrm {ac1}} \ \)を表す式を\( \ V_{1}\),\(I_{\mathrm {d}}\),及び\( \ \alpha _{1} \ \)を用いて示せ。
(4) ①系統に流れる波高値\( \ I_{\mathrm {d}} \ \)の交流の線電流は半サイクルで\( \ 120° \ \)通電の方形波となり,この波形に含まれる基本波実効値\( \ I_{1} \ \)は\(\displaystyle \frac {\sqrt {6}}{\pi } I_{\mathrm {d}} \ \)である。この基本波による①系統からの遅れの無効電力\( \ Q_{\mathrm {ac1}} \ \)を表す式を,\(V_{1}\),\(I_{\mathrm {d}}\)及び\( \ \alpha _{1} \ \)を用いて示せ。
(5) 変換器\(2\)の直流電圧\( \ v_{\mathrm {dc2}} \ \)の平均値を\( \ V_{\mathrm {dc2}} \ \)とする。①系統から②系統に電力を送る場合,電流\( \ I_{\mathrm {d}} \ \)の極性は正,平均電圧\( \ V_{\mathrm {dc1}}\),\(V_{\mathrm {dc2}} \ \)の両方の極性とも正である。
逆に②系統から①系統に電力を送る場合,電流\( \ I_{\mathrm {d}}\),平均電圧\( \ V_{\mathrm {dc1}}\),\(V_{\mathrm {dc2}} \ \)の極性は正であるか負であるかを示せ。
【ワンポイント解説】
三相サイクロコンバータに関する問題です。平均値の導出は結果がほぼ決まっているため,内容を理解している方が解くと,かなりの確率で完答できると思います。全波整流回路の動作について,どのようになるか整理して理解しましょう。
1.全波整流回路のスイッチ動作
全波整流回路は図3のように\(120°\)ずつサイリスタが切り替わり,正側と負側が交互にスイッチングする回路となっています。これにより,問題図2に示すような\(60°\)ずつの波形のような直流電圧が得られます。本問はこれを理解していることが前提となった問題となっています。
2.平均値
\(f( \theta )\)を周期\(T \)の周期関数であるとしたとき,平均値\(F_{\mathrm {av}}\)は以下の通りとなります。
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T }f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
3.加法定理
サインとコサインの加法定理は電験二種以上では必須となります。
\[
\begin{eqnarray}
\sin \left( \alpha ±\beta \right) &=&\sin \alpha \cos \beta ±\cos \alpha \sin \beta \\[ 5pt ]
\cos \left( \alpha ±\beta \right) &=&\cos \alpha \cos \beta ∓\sin \alpha \sin \beta \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)\( \ \mathrm {T}_{1} \ \)及び\( \ \mathrm {T}_{5} \ \)がオンしていた\( \ 120° \ \)に相当する時間後に通電しているのはどのサイリスタか
ワンポイント解説「1.全波整流回路のスイッチ動作」の通り,\( \ \mathrm {T}_{1} \ \)及び\( \ \mathrm {T}_{5} \ \)がオンしていた\( \ 120° \ \)に相当する時間後に通電しているのは\( \ \mathrm {T}_{2} \ \)及び\( \ \mathrm {T}_{6} \ \)となる。
(2)直流電圧\( \ v_{\mathrm {dc1}} \ \)の平均値\( \ V_{\mathrm {dc1}}\)
この整流回路は\(\displaystyle \frac {\pi }{3}\)ずつ同じ波形を描いているので,\(\displaystyle -\frac {\pi }{6}+\alpha _{1}\)から\(\displaystyle \frac {\pi }{6}+\alpha _{1}\)までの平均値を求めればよい。
ワンポイント解説「2.平均値」より,
\[
\begin{eqnarray}
V_{\mathrm {dc1}}&=&\frac {1}{\frac {\pi }{3}}\int _{-\frac {\pi }{6}+\alpha _{1}}^{\frac {\pi }{6}+\alpha _{1}}\sqrt {2}V_{1}\cos \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\int _{-\frac {\pi }{6}+\alpha _{1}}^{\frac {\pi }{6}+\alpha _{1}}\cos \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ \sin \theta \right] _{-\frac {\pi }{6}+\alpha _{1}}^{\frac {\pi }{6}+\alpha _{1}} \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ \sin \left( \frac {\pi }{6}+\alpha _{1}\right) -\sin \left( -\frac {\pi }{6}+\alpha _{1}\right) \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ \left( \sin \frac {\pi }{6} \cos \alpha _{1}+\cos \frac {\pi }{6}\sin \alpha _{1}\right) -\left( \sin \left( -\frac {\pi }{6}\right) \cos \alpha _{1}+\cos \left( -\frac {\pi }{6}\right) \sin \alpha _{1}\right) \right] \\[ 5pt ]
\end{eqnarray}
\]
ここで,\(\displaystyle \sin \frac {\pi }{6}=-\sin \left( -\frac {\pi }{6}\right) \),\(\displaystyle \cos \frac {\pi }{6}=\cos \left( -\frac {\pi }{6}\right) \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {dc1}}&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ \left( \sin \frac {\pi }{6} \cos \alpha _{1}+\cos \frac {\pi }{6}\sin \alpha _{1}\right) -\left( -\sin \frac {\pi }{6} \cos \alpha _{1}+\cos \frac {\pi }{6} \sin \alpha _{1}\right) \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ 2 \sin \frac {\pi }{6} \cos \alpha _{1} \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\left[ 2 \times \frac {1}{2} \cos \alpha _{1} \right] \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}}{\pi }\cos \alpha _{1} \\[ 5pt ]
&≒&1.35V_{1}\cos \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※この平均値の式は暗記していた方が良い式ですが,試験では途中の計算過程が必要となりますので,導出できるようにしておいて下さい。
(3)有効電力\( \ P_{\mathrm {ac1}} \ \)を表す式を\( \ V_{1}\),\(I_{\mathrm {d}}\),及び\( \ \alpha _{1} \ \)を用いて示す
題意より,有効電力\( \ P_{\mathrm {ac1}} \ \)と直流電力\( \ P_{\mathrm {dc}} \ \)は等しいので,直流電力を求めればよい。よって,(2)解答式を利用すると,
\[
\begin{eqnarray}
P_{\mathrm {ac1}}&=&P_{\mathrm {dc}} \\[ 5pt ]
&=&V_{\mathrm {dc1}}I_{\mathrm {d}} \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}I_{\mathrm {d}}}{\pi }\cos \alpha _{1} \\[ 5pt ]
&≒&1.35V_{1}I_{\mathrm {d}}\cos \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)遅れの無効電力\( \ Q_{\mathrm {ac1}} \ \)を表す式を,\(V_{1}\),\(I_{\mathrm {d}}\),及び\( \ \alpha _{1} \ \)を用いて示す
有効電力\( \ P_{\mathrm {ac1}} \ \)は,\(V_{1}\),\(I_{1}\),\( \ \alpha _{1} \ \)を用いて表すと,
\[
\begin{eqnarray}
P_{\mathrm {ac1}}&=&\sqrt {3}V_{1}I_{1}\cos \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
で表されるから,これに\( \ I_{1} =\displaystyle \frac {\sqrt {6}}{\pi } I_{\mathrm {d}} \ \)を代入すると,
\[
\begin{eqnarray}
P_{\mathrm {ac1}}&=&\sqrt {3}V_{1}\times \frac {\sqrt {6}}{\pi } I_{\mathrm {d}}\cos \alpha _{1} \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}I_{\mathrm {d}}}{\pi }\cos \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,(3)の解答と一致する。したがって,遅れの無効電力\( \ Q_{\mathrm {ac1}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {ac1}}&=&\sqrt {3}V_{1}I_{1}\sin \alpha _{1} \\[ 5pt ]
&=&\sqrt {3}V_{1}\times \frac {\sqrt {6}}{\pi } I_{\mathrm {d}}\sin \alpha _{1} \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{1}I_{\mathrm {d}}}{\pi }\sin \alpha _{1} \\[ 5pt ]
&≒&1.35V_{1}I_{\mathrm {d}}\sin \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)②系統から①系統に電力を送る場合,電流\( \ I_{\mathrm {d}}\),平均電圧\( \ V_{\mathrm {dc1}}\),\(V_{\mathrm {dc2}} \ \)の極性は正であるか負であるかを示す
サイリスタの向きを考慮すると,②系統側から①系統に電力を送る場合,電圧は正負が反転し,電流は同じ右回りの方向を流れる。
したがって,電流\( \ I_{\mathrm {d}}\)は正,平均電圧\( \ V_{\mathrm {dc1}}\),\(V_{\mathrm {dc2}} \ \)は負となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは