《理論》〈電子理論〉[H24:問8]演算増幅器を用いた負性抵抗回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，演算増幅器を用いた負性抵抗回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。

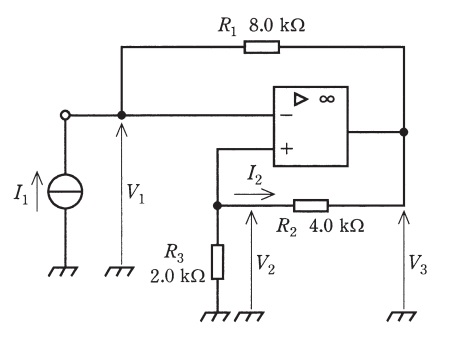
図の回路において，演算増幅器の入力端子には電流が流れ込まないので，抵抗\( \ R_{2} \ \)と抵抗\( \ R_{3} \ \)に流れる電流は等しい。このため，\( \ V_{3} \ \)は\( \ V_{2} \ \)の\( \ \fbox {　 （１） 　} \ \)倍となる。また，演算増幅器の入力端子の電位\( \ V_{1} \ \)と\( \ V_{2} \ \)は等しいので，抵抗\( \ R_{1} \ \)と抵抗\( \ R_{2} \ \)の両端の電位差も等しい。したがって，電流\( \ I_{1} \ \)を\( \ 0.10 \ \mathrm {[mA]} \ \)とすると，抵抗\( \ R_{2} \ \)に流れる電流\( \ I_{2} \ \)は\( \ \fbox {　 （２） 　} \ \mathrm {[mA]} \ \)であることがわかる。このとき，\( \ V_{2} \ \)は\( \ \fbox {　 （３） 　} \ \mathrm {[V]} \ \)であり，\( \ V_{3} \ \)は\( \ \fbox {　 （４） 　} \ \mathrm {[V]} \ \)である。さらに，演算増幅器の入力端子の電位\( \ V_{1} \ \)が\( \ V_{2} \ \)に等しいことから，\( \ \displaystyle \frac {V_{1}}{I_{1}} \ \)が\( \ \fbox {　 （５） 　} \ \mathrm {[k\Omega ]} \ \)であることがわかる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　-4.0　　　　　　&（ロ）&　-3.0　　　　　　　&（ハ）&　-1.2 \\[ 5pt ] &（ニ）&　-0.50　　　&（ホ）&　-0.40　　　　&（ヘ）&　-0.30 \\[ 5pt ] &（ト）&　-0.20　　　&（チ）&　0.20　　　　&（リ）&　0.30 \\[ 5pt ] &（ヌ）&　0.40　　　&（ル）&　0.50　　　&（ヲ）&　1.2 \\[ 5pt ] &（ワ）&　2.0　　　&（カ）&　3.0 　　　&（ヨ）&　4.0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

演算増幅器からの出題です。演算増幅器の基本を理解した上で，問題パターンを理解すると，演算増幅器の問題は非常に得点源になります。

1.理想的な演算増幅器の特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

【解答】

(1)解答：カ
分圧の法則より，
\[
\begin{eqnarray}
V_{2}&=&\frac {R_{3}}{R_{2}+R_{3}}V_{3} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
V_{3}&=&\frac {R_{2}+R_{3}}{R_{3}}V_{2} \\[ 5pt ] &=&\frac {4.0+2.0}{2.0}V_{2} \\[ 5pt ] &=&3V_{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
演算増幅器の入力端子に電流は流れないので，抵抗\( \ R_{1} \ \)には電流\( \ I_{1} \ \)がそのまま流れる。題意より，抵抗\( \ R_{1} \ \)と抵抗\( \ R_{2} \ \)の両端の電位差が等しいので，
\[
\begin{eqnarray}
R_{1}I_{1}&=&R_{2}I_{2} \\[ 5pt ] I_{2}&=&\frac {R_{1}}{R_{2}}I_{1} \\[ 5pt ] &=&\frac {8.0}{4.0}\times 0.10 \\[ 5pt ] &=&0.20 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
\( \ R_{3} \ \)に流れる電流も\( \ I_{2}=0.20 \ \mathrm {[mA]} \ \)なので，
\[
\begin{eqnarray}
V_{2}&=&0-R_{3}I_{2} \\[ 5pt ] &=&0-2.0\times 10^{3}\times 0.20\times 10^{-3} \\[ 5pt ] &=&-0.40 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
(3)と同様に\( \ V_{3} \ \)は，
\[
\begin{eqnarray}
V_{3}&=&V_{2}-R_{2}I_{2} \\[ 5pt ] &=&-0.40-4.0\times 10^{3}\times 0.20\times 10^{-3} \\[ 5pt ] &=&-1.2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：イ
\( \ V_{1} \ \)が\( \ V_{2} \ \)に等しいので，
\[
\begin{eqnarray}
\frac {V_{1}}{I_{1}}&=&\frac {V_{2}}{I_{1}} \\[ 5pt ] &=&\frac {-0.40}{0.10\times 10^{-3}} \\[ 5pt ] &=&-4.0\times 10^{3} \ \mathrm {[\Omega ]}　→　-4.0 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。