Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のように三相交流送電線(単線結線図)と通信線があり,その間に遮へい線がある。送電線と通信線の相互インピーダンスを\( \ {\dot Z}_{\mathrm {12}} \ \),送電線と遮へい線との相互インピーダンスを\( \ {\dot Z}_{\mathrm {1S}} \ \),遮へい線と通信線の相互インピーダンスを\( \ {\dot Z}_{\mathrm {2S}} \ \),遮へい線の自己インピーダンスを\( \ {\dot Z}_{\mathrm {S}} \ \)とする。一線地絡事故により送電線に流れる零相電流を\( \ {\dot I}_{\mathrm {0}} \ \)とするとき次の問に答えよ。
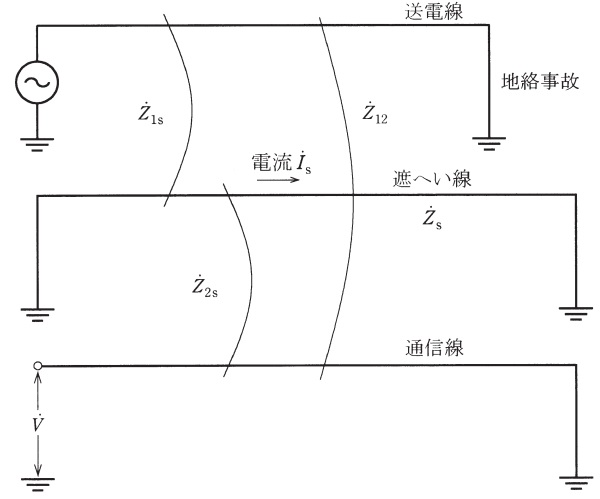
(1) 遮へい線が無い場合に,通信線の開放端に生じる誘導電圧\( \ \dot V \ \)を求めよ。
(2) 遮へい線が存在する場合に,遮へい線に流れる電流\( \ {\dot I}_{\mathrm {S}} \ \)と通信線の開放端に生じる誘導電圧\( \ {\dot V}^{\prime } \ \)を求めよ。
(3) (2)の計算結果を用いて,遮へい線をどのように配置するのが良いか説明せよ。
【ワンポイント解説】
送電線から通信線への電磁誘導障害に関する問題です。
知識として遮へい線を設けることや遮へい線を通信線寄りにした方が良いということを知っている人も多いかもしれませんが,二次試験になるとさらに「なぜ」遮へい線が効果があるのかを学習することが必要になります。
メカニズムを理解するには非常に良い問題であると思いますので,確実に理解するようにしましょう。
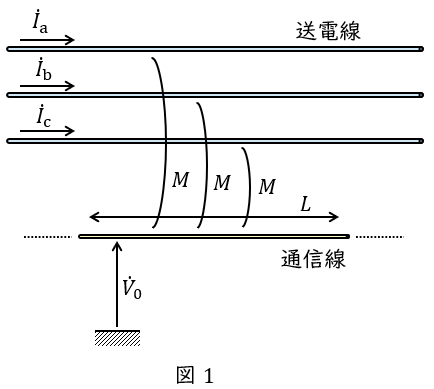
1.電磁誘導障害
送電線と通信線との相互インダクタンスと送電線に流れる各電流の電磁誘導により誘導電圧が発生します。
定量的には,図1のように各電流と相互インダクタンス\( \ M \ \mathrm {[H/m]} \ \)と並行区間長\( \ L \ \mathrm {[m]} \ \)を定めると,通信線に発生する電圧\( \ {\dot V}_{0} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{0}&=&\mathrm {j}\omega ML {\dot I}_{\mathrm {a}}+\mathrm {j}\omega ML {\dot I}_{\mathrm {b}}+\mathrm {j}\omega ML {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=&\mathrm {j}\omega ML \left( {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} \right)
\end{eqnarray}
\]
となります。通常運転時,\( \ {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} ≒0 \ \)であるので,\( \ {\dot V}_{0}≒0 \ \)となりますが,事故等で三相不平衡状態になると電磁誘導障害が発生することになります。
2.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータとは,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,\( \ 1+a+a^{2}=0 \ \)となります。
3.対称座標法
故障計算をする際に,非常に便利な方法で,以下のように定義されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。ただし,\( \ a \ \)はベクトルオペレータとなります。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)遮へい線が無い場合に,通信線の開放端に生じる誘導電圧\( \ \dot V \ \)
各相の電流を\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \),送電線と通信線の相互インダクタンスを\( \ M \ \mathrm {[H]} \ \),電源の角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)をとすると,通信線の開放端に生じる誘導電圧\( \ \dot V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\dot V&=&\mathrm {j}\omega M {\dot I}_{\mathrm {a}}+\mathrm {j}\omega M {\dot I}_{\mathrm {b}}+\mathrm {j}\omega M {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=&\mathrm {j}\omega M \left( {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} \right) ・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.対称座標法」より,零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺の和を取ると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} &=&3{\dot I}_{0}+\left( 1+a+a^{2}\right) {\dot I}_{1} +\left( 1+a+a^{2}\right) {\dot I}_{2} \\[ 5pt ]
&=&3{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ {\dot Z}_{\mathrm {12}}=\mathrm {j}\omega M \ \)であるので,それぞれ①式に代入すると,
\[
\begin{eqnarray}
\dot V&=&\mathrm {j}\omega M \left( {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} \right) \\[ 5pt ]
&=&{\dot Z}_{\mathrm {12}}\cdot 3{\dot I}_{0} \\[ 5pt ]
&=&3{\dot Z}_{\mathrm {12}}{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)遮へい線が存在する場合に,遮へい線に流れる電流\( \ {\dot I}_{\mathrm {S}} \ \)と通信線の開放端に生じる誘導電圧\( \ {\dot V}^{\prime } \ \)
(1)と同様に遮へい線に誘導される誘導電圧\( \ {\dot V}_{\mathrm {S}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {S}}&=&3{\dot Z}_{\mathrm {1S}}{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
であり,遮へい線に流れる電流\( \ {\dot I}_{\mathrm {S}} \ \)は,\( \ {\dot I}_{\mathrm {0}} \ \)による誘導電圧を打ち消すように流れるので,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {S}}&=&-\frac {{\dot V}_{\mathrm {S}}}{{\dot Z}_{\mathrm {S}}} \\[ 5pt ]
&=&-\frac {3{\dot Z}_{\mathrm {1S}}{\dot I}_{0}}{{\dot Z}_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,通信線の開放端に生じる誘導電圧\( \ {\dot V}^{\prime } \ \)は(1)の送電線による誘導電圧と遮へい線による誘導電圧の和となるので,
\[
\begin{eqnarray}
{\dot V}^{\prime }&=&3{\dot Z}_{\mathrm {12}}{\dot I}_{0}+{\dot Z}_{\mathrm {2S}}{\dot I}_{\mathrm {S}} \\[ 5pt ]
&=&3{\dot Z}_{\mathrm {12}}{\dot I}_{0}+{\dot Z}_{\mathrm {2S}}\left( -\frac {3{\dot Z}_{\mathrm {1S}}{\dot I}_{0}}{{\dot Z}_{\mathrm {S}}}\right) \\[ 5pt ]
&=&3{\dot Z}_{\mathrm {12}}{\dot I}_{0}-\frac {3{\dot Z}_{\mathrm {1S}}{\dot Z}_{\mathrm {2S}}{\dot I}_{0}}{{\dot Z}_{\mathrm {S}}} \\[ 5pt ]
&=&3{\dot Z}_{\mathrm {12}}{\dot I}_{0}\left( 1-\frac {{\dot Z}_{\mathrm {1S}}{\dot Z}_{\mathrm {2S}}}{{\dot Z}_{\mathrm {12}}{\dot Z}_{\mathrm {S}}}\right) \\[ 5pt ]
&=&\dot V\left( 1-\frac {{\dot Z}_{\mathrm {1S}}{\dot Z}_{\mathrm {2S}}}{{\dot Z}_{\mathrm {12}}{\dot Z}_{\mathrm {S}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)(2)の計算結果を用いて,遮へい線をどのように配置するのが良いか説明する
(2)の計算結果より,送電線の近傍に設置すると,\( \ {\dot Z}_{\mathrm {12}}≒{\dot Z}_{\mathrm {2S}} \ \)となるので,送電線近傍に設置した場合の誘導電圧\( \ {\dot V}^{\prime }_{\mathrm {T}} \ \)は,
\[
\begin{eqnarray}
{\dot V}^{\prime }_{\mathrm {T}}&=&\dot V\left( 1-\frac {{\dot Z}_{\mathrm {1S}}}{{\dot Z}_{\mathrm {S}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,通信線の近傍に設置すると,\( \ {\dot Z}_{\mathrm {12}}≒{\dot Z}_{\mathrm {1S}} \ \)となるので,通信線近傍に設置した場合の誘導電圧\( \ {\dot V}^{\prime }_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
{\dot V}^{\prime }_{\mathrm {C}}&=&\dot V\left( 1-\frac {{\dot Z}_{\mathrm {2S}}}{{\dot Z}_{\mathrm {S}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ {\dot Z}_{\mathrm {1S}} \ \)及び\( \ {\dot Z}_{\mathrm {2S}} \ \)は遮へい線との離隔距離が小さくなればなるほど相互インピーダンス(∝相互インダクタンス)が大きくなり,より自己インピーダンス\( \ {\dot Z}_{\mathrm {S}} \ \)の値に近づく。したがって,どちらの場合も離隔距離が小さくなれば小さくなるほど,通信線に誘導される電圧も小さくなる。
実際には遮へい線を送電線の近くに設置する場合,その電圧差により離隔距離を一定以上小さくできないので,通信線近傍に設置した方が良いこととなる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは