【問題】
【難易度】★★★☆☆(普通)
図のように変電所から,皮相電力\(100 \ \mathrm {MV\cdot A}\),遅れ力率\(80 \ %\)の負荷に電力を供給している。変圧器の一次,二次及び三次の定格線間電圧は\(154 \ \mathrm {kV}\),\(77 \ \mathrm {kV}\),\(22 \ \mathrm {kV}\)であり,巻線の結線は,一次側\(\mathrm {Y}\)結線,二次側\(\mathrm {Y}\)結線,三次側\(\mathrm {\Delta }\)結線である。変圧器の三次には\(30 \ \mathrm {Mvar}\)の進相コンデンサが接続されている。変圧器の容量及び\(%\)インピーダンスは以下のとおりとする。
\[
\begin{eqnarray}
・容量 一次 \ 200 \ \mathrm {MV\cdot A} 二次 \ 200 \ \mathrm {MV\cdot A} 三次 \ 50 \ \mathrm {MV\cdot A} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
・%インピーダンス &一次-二次& &15 \ %& &\left( 200 \ \mathrm {MV\cdot A}ベース\right)& \\[ 5pt ]
&一次-三次& & \ \ 8 \ %& &\left( 200 \ \mathrm {MV\cdot A}ベース\right) & \\[ 5pt ]
&二次-三次& & \ \ 2 \ %& &\left( \ \ 50 \ \mathrm {MV\cdot A}ベース\right) & \\[ 5pt ]
\end{eqnarray}
\]
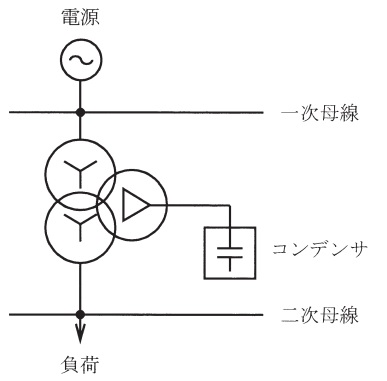
(1) 二次-三次巻線間の%インピーダンスの\(\mathrm {p.u.}\)値を一次容量基準で表せ。
(2) 一次,二次及び三次巻線の%インピーダンスの\(\mathrm {p.u.}\)値をそれぞれ一次容量基準で表せ。
(3) 一次母線の電圧が\(152 \ \mathrm {kV}\)の場合,二次母線の電圧を求めよ。
ただし,変圧器のタップは一次\(154 \ \mathrm {kV}\) / 二次\(77 \ \mathrm {kV}\)とする。また,変圧器の励磁電流や有効電力による電圧への影響は考慮しなくてよく,巻線リアクタンスでの無効電力消費は無視する。なお,電圧降下が十分に小さいとして,簡略な計算法を用いてよい。
【ワンポイント解説】
(3)の百分率インピーダンスにおける電圧降下の簡略な計算式を知っているかが,この問題の攻略の大きなポイントとなると思います。式の導出は電験一種レベルなので,二種では覚えるだけでも良いと思います。
1.%インピーダンスの基準容量変換
基準容量\(P_{\mathrm {B}}\)で百分率インピーダンスが\(%Z_{\mathrm {B}}\)であるとき基準容量\(P_{\mathrm {A}}\)での百分率インピーダンス\(%Z_{\mathrm {A}}\)は,
\[
\begin{eqnarray}
%Z_{\mathrm {A}}=\frac {P_{\mathrm {A}}}{P_{\mathrm {B}}}%Z_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
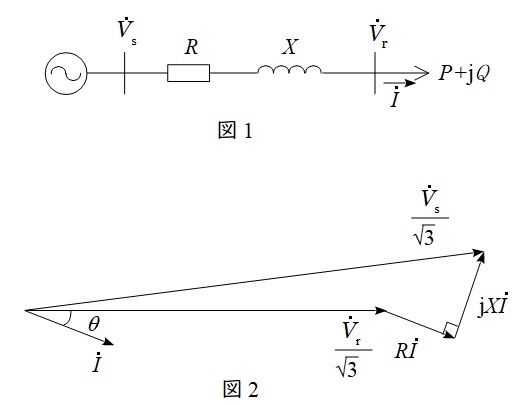
2.\( \ \mathrm {p.u. } \ \)法における送電線の電圧降下の簡略式
図1,図2のように示される系統図及びベクトル図において,\( \ {\dot V}_{\mathrm {s}} \ \)と\( \ {\dot V}_{\mathrm {r}} \ \)の位相差がほぼ無視できるとすると,
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P=\sqrt {3}V_{\mathrm {r}}I\cos \theta \ \),\( \ Q=\sqrt {3}V_{\mathrm {r}}I\sin \theta \ \)の関係があるので,
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&=&\frac {V_{\mathrm {r}}}{\sqrt {3}}+\frac {RP}{\sqrt {3}V_{\mathrm {r}}} +\frac {XQ}{\sqrt {3}V_{\mathrm {r}}} \\[ 5pt ]
V_{\mathrm {s}}&=&V_{\mathrm {r}}+\frac {RP}{V_{\mathrm {r}}} +\frac {XQ}{V_{\mathrm {r}}} \\[ 5pt ]
V_{\mathrm {s}}V_{\mathrm {r}}&=&V_{\mathrm {r}}^{2}+RP+XQ \\[ 5pt ]
V_{\mathrm {r}}^{2}-V_{\mathrm {s}}V_{\mathrm {r}}+RP+XQ&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となります。上式を\( \ V_{\mathrm {r}} \ \)について解くと,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&\frac {V_{\mathrm {s}}±\sqrt {V_{\mathrm {s}}^{2}-4\left( RP+XQ\right) }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで,\( \ V_{\mathrm {s}}≒1 \ \mathrm {[p.u.]} \ \)であるとすると,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&\frac {1±\sqrt {1-4\left( RP+XQ\right) }}{2} \\[ 5pt ]
&≃&\frac {1 ± \left\{ 1-2\left( RP+XQ\right) \right\} }{2} \\[ 5pt ]
&=&1-\left( RP+XQ\right) \left( RP+XQは不適\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,電圧降下\( \ \Delta v \ \)は\( \ \Delta v=RP+XQ \ \)で近似されます。
【関連する「電気の神髄」記事】
【解答】
(1)二次-三次巻線間の%インピーダンスの\(\mathrm {p.u.}\)値
ワンポイント解説「1.%インピーダンスの基準容量変換」より,二次-三次巻線間の%インピーダンス\(%X_{23}\)\(\left( 200 \ \mathrm {MV\cdot A}ベース\right) \)は,
\[
\begin{eqnarray}
%X_{23}&=&\frac {200}{50}\times 2 \\[ 5pt ]
&=&8 \ [%] → 0.08 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)一次,二次及び三次巻線の%インピーダンスの\(\mathrm {p.u.}\)値
一次,二次及び三次巻線の%インピーダンスの\(\mathrm {p.u.}\)値を\(X_{1}\),\(X_{2}\),\(X_{3}\)とすると,
\[
\begin{eqnarray}
X_{1}+X_{2}&=&0.15 \\[ 5pt ]
X_{1}+X_{3}&=&0.08 \\[ 5pt ]
X_{2}+X_{3}&=&0.08 \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを解くと,
\[
\begin{eqnarray}
X_{1}&=&0.075 \ [ \mathrm {p.u.} ] \\[ 5pt ]
X_{2}&=&0.075 \ [ \mathrm {p.u.} ] \\[ 5pt ]
X_{3}&=&0.005 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)一次母線の電圧が\(152 \ \mathrm {kV}\)の場合,二次母線の電圧
一次母線の電圧の\(\mathrm {p.u.}\)値\(V_{\mathrm {1p.u.}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {1p.u.}}&=&\frac {152}{154} \\[ 5pt ]
&≒&0.98701 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
となる。皮相電力が\(100 \ \mathrm {MV\cdot A}\),遅れ力率\(80 \ %\)であるから,負荷に供給される無効電力の大きさ\(Q_{\mathrm {L}}\)は,
\[
\begin{eqnarray}
Q_{\mathrm {L}}&=&100\times \sqrt {1-0.8^{2}} \\[ 5pt ]
&=&60 \ [ \mathrm {Mvar} ] \\[ 5pt ]
\end{eqnarray}
\]
であるから,その\(\mathrm {p.u.}\)値は,
\[
\begin{eqnarray}
Q_{\mathrm {L}}&=&\frac {60}{200} \\[ 5pt ]
&=&0.3 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
となる。三次側母線のコンデンサの容量の\(\mathrm {p.u.}\)値\(Q\)は遅れを正とすると,
\[
\begin{eqnarray}
Q&=&-\frac {30}{200} \\[ 5pt ]
&=&-0.15 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
となる。
よって,一次二次母線間の電圧降下\(\Delta V_{12}\)は,
\[
\begin{eqnarray}
\Delta V_{12}&=&X_{1} \times \left( Q_{\mathrm {L}}+Q\right) +X_{2}Q_{\mathrm {L}} \\[ 5pt ]
&=&0.075 \times \left( 0.3-0.15\right) +0.075\times 0.3 \\[ 5pt ]
&=&0.03375 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,二次側母線電圧\(V_{\mathrm {2p.u.}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {2p.u.}}&=&V_{\mathrm {1p.u.}}-\Delta V_{12} \\[ 5pt ]
&=&0.98701-0.03375 \\[ 5pt ]
&=&0.95326 \ [ \mathrm {p.u.} ] \\[ 5pt ]
\end{eqnarray}
\]
となるので,二次側母線電圧\(V_{\mathrm {2}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {2}}&=&77\times V_{\mathrm {2p.u.}} \\[ 5pt ]
&=&77\times 0.95326 \\[ 5pt ]
&≒&73.4 \ [ \mathrm {kV} ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは