Contents
【問題】
【難易度】★★★★☆(やや難しい)
等面積法を用いた過渡安定性の計算に関して,次の問に答えよ。
図1のように,変圧器及び\( \ 2 \ \)回線送電線を介して,同期発電機から無限大母線へ三相\( \ 3 \ \)線式で送電する系統を考える。変圧器のリアクタンスは\( \ X_{\mathrm {t}} \ \mathrm {[p.u.]} \ \),送電線\( \ 1 \ \)回線当たりのリアクタンスを\( \ X_{l} \ \mathrm {[p.u.]} \ \),同期発電機のリアクタンスは系統じょう乱の影響によらず過渡リアクタンス\( \ X_{\mathrm {d}}^{\prime } \ \mathrm {[p.u.]} \ \)で一定とし,いずれも抵抗や静電容量は無視する。同期発電機の内部電圧及び無限大母線の電圧の大きさはそれぞれ\( \ E_{\mathrm {G}} \ \mathrm {[p.u.]} \ \)及び\( \ E_{\mathrm {0}} \ \mathrm {[p.u.]} \ \)で一定とし,同期発電機の発電出力(電気的出力)及びその初期値をそれぞれ\( \ P_{\mathrm {G}} \ \mathrm {[p.u.]} \ \)及び\( \ P_{\mathrm {G0}} \ \mathrm {[p.u.]} \ \)とする。無限大母線の電圧を位相の基準,単位法による定数は全て同一の基準容量に基づくものとして,以下の問に答えよ。
(1) 発電機内部電圧の位相角を\( \ \delta _{\mathrm {0}} \ \mathrm {[rad]} \ \)として,同期発電機の発電出力\( \ P_{\mathrm {G}} \ \)を表す数式を\( \ E_{\mathrm {G}} \ \),\( \ E_{\mathrm {0}} \ \),\( \ X_{\mathrm {d}}^{\prime } \ \),\( \ X_{\mathrm {t}} \ \),\( \ X_{l} \ \),\( \ \delta _{\mathrm {0}} \ \)を用いて記載せよ。
以降の設問では,\( \ X_{\mathrm {t}}=0.10 \ \mathrm {p.u.} \ \),\( \ X_{l}=0.20 \ \mathrm {p.u.} \ \),\( \ X_{\mathrm {d}}^{\prime }=0.15 \ \mathrm {p.u.} \ \),\( \ E_{\mathrm {G}}=E_{\mathrm {0}}=1.0 \ \mathrm {p.u.} \ \),\( \ P_{\mathrm {G0}}=0.8 \ \mathrm {p.u.} \ \)とする。また,発電機への機械的入力は\( \ P_{\mathrm {G0}} \ \)に等しく,かつ,一定とする。\( \ \pi =3.14 \ \)として計算し,有効桁数を\( \ 2 \ \)桁として答えよ。なお,同期発電機が定常状態にある平衡点では発電機内部電圧の位相角は小さいとみなし,\( \ \sin \delta ≈ \delta \ \)の近似を用いてよい。
(2) 同期発電機の内部電圧の位相角\( \ \delta _{\mathrm {0}} \ \mathrm {[rad]} \ \)を求めよ。
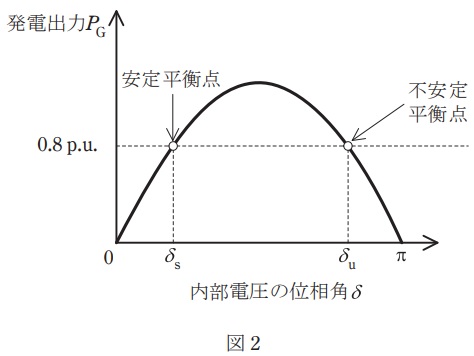
(3) 図1の送電線\( \ 1 \ \)回線で三相地絡故障が生じ,その後,当該の回線が両端の遮断器の動作により切り離されることを想定する。\( \ 1 \ \)回線開放後の不安定平衡点における位相角\( \ \delta _{\mathrm {u}} \ \mathrm {[rad]} \ \)を求めよ。ここで,\( \ 1 \ \)回線開放後の系統における発電出力と内部電圧の位相角との関係を図2に示す。同図の安定平衡点における位相角を\( \ \delta _{\mathrm {s}} \ \mathrm {[rad]} \ \)とし,\( \ \delta _{\mathrm {u}}=\pi – \delta _{\mathrm {s}} \ \)を用いること。
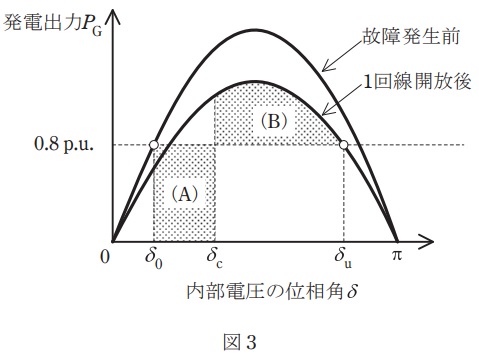
(4) 小問(3)の故障が生じた際,故障継続中の同期発電機の発電出力を\( \ 0 \ \mathrm {p.u.} \ \)とすると,同期発電機の位相角が図3の\( \ \delta _{\mathrm {c}} \ \mathrm {[rad]} \ \)に到達する前に当該の回線を開放できれば脱調を回避できる。ここで\( \ \delta _{\mathrm {c}} \ \mathrm {[rad]} \ \)は,等面積法により同図中の面積(A)と(B)が等しくなる位相角である。\( \ \cos \delta _{\mathrm {c}} \ \) の値を求めよ。ただし,同期発電機の制動効果は無視する。

【ワンポイント解説】
同期発電機の過渡安定度の検討に関する問題です。
(3)までは比較的解きやすい問題ですが,(4)の計算は途中の近似式を工夫する等高い数学能力が求められる問題です。合格のためには(4)は本番で解かずに他の問題を優先しても良いかと思います。
1.同期発電機の出力
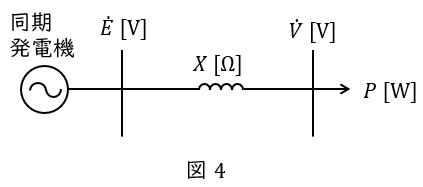
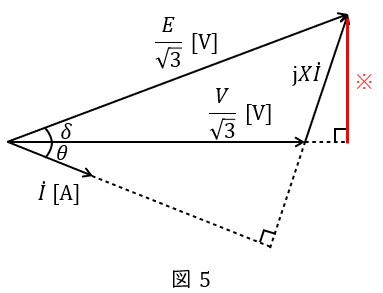
同期発電機の内部誘導起電力が\( \ E \ \mathrm {[V]} \ \),端子電圧が\( \ V \ \mathrm {[V]} \ \),\( \ 1 \ \)相あたりの同期リアクタンスが\( \ X \ \mathrm {[\Omega ]} \ \)(抵抗分は無視できるものとします),電機子電流が\( \ I \ \mathrm {[A]} \ \)であるとすると,回路図は図4,ベクトル図は図5のように描くことができます。ただし,\( \ \delta \ \mathrm {[rad]} \ \)は内部誘導起電力と端子電圧の相差角,\( \ \theta \ \mathrm {[rad]} \ \)は力率角です。
このとき,発電機の出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3} VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
で求めることができ,図5の※線を求める式より,
\[
\begin{eqnarray}
XI\cos \theta &=&\frac {E}{\sqrt {3}}\sin \delta \\[ 5pt ]
I\cos \theta &=&\frac {E}{\sqrt {3}X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P&=&\sqrt {3} VI\cos \theta \\[ 5pt ]
&=&\sqrt {3} V\cdot \frac {E}{\sqrt {3}X}\sin \delta \\[ 5pt ]
&=&\frac {EV}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。上式は\( \ P=\sqrt {3} VI\cos \theta \ \)と合わせて公式として覚えておきましょう。
2.同期化力
同期発電機の同期外れの起こりにくさを表すもので,出力\( \ P \ \mathrm {[W]} \ \)を相差角\( \ \delta \ \mathrm {[rad]} \ \)で微分した\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } \ \)で求められます。したがって,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {EV}{X}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }>0 \ \)のとき安定,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }<0 \ \)のとき不安定,すなわち\( \ \displaystyle 0 < \delta < \frac {\pi }{2} \ \)のとき安定,\( \ \displaystyle \frac {\pi }{2} < \delta < \pi \ \)のとき不安定となります。

3.等面積法
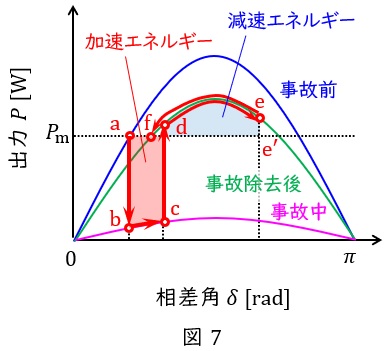
過渡安定度のメカニズムの説明には,出力\( \ P \ \mathrm {[W]} \ \)と相差角\( \ \delta \ \mathrm {[rad]} \ \)の関係\( \ \left( \displaystyle P=\frac {EV}{X}\sin \delta \right) \ \)を表す図7のような\( \ P-\delta \ \)曲線による等面積法が用いられます。
図7の\( \ \mathrm {a} \ \)で安定運転していた発電機に事故が発生すると,多量の無効電力が流れ,\( \ \mathrm {b} \ \)点に移動します。事故を除去する\( \ \mathrm {c} \ \)点まで発電機は加速し,事故除去後,線路は一相分なくなる分事故前よりリアクタンスが大きくなるため,\( \ P-\delta \ \)曲線は緑線になり,\( \ \mathrm {d} \ \)点に移動します。その後,発電機は減速エネルギーが働き始め,\( \ \mathrm {e} \ \)点まで進むと減速を開始し,元の出力と同じ\( \ \mathrm {f} \ \)点まで行くと発電機は安定します。減速エネルギーが足りず,\( \ \mathrm {e}^{\prime } \ \)点まで行ってしまうと脱調します。
したがって,加速エネルギーを大きくしないためには,超速応励磁方式を採用し\( \ \mathrm {b} \ \)点から\( \ \mathrm {c} \ \)点までの距離を短くすることが効果的となります。
【解答】
(1)同期発電機の発電出力\( \ P_{\mathrm {G}} \ \)を表す数式
同期発電機から無限大母線までのリアクタンス\( \ X \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
X&=&X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+\frac {X_{l}\cdot X_{l}}{X_{l}+X_{l}} \\[ 5pt ]
&=&X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+\frac {X_{l}}{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,同期発電機の発電出力\( \ P_{\mathrm {G}} \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「1.同期発電機の出力」の通り,
\[
\begin{eqnarray}
P_{\mathrm {G}}&=&\frac {E_{\mathrm {G}}E_{\mathrm {0}}}{X}\sin \delta _{\mathrm {0}} \\[ 5pt ]
&=&\frac {E_{\mathrm {G}}E_{\mathrm {0}}}{\displaystyle X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+\frac {X_{l}}{2}}\sin \delta _{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)同期発電機の内部電圧の位相角\( \ \delta _{\mathrm {0}} \ \mathrm {[rad]} \ \)
(1)解答式より,
\[
\begin{eqnarray}
\sin \delta _{\mathrm {0}}&=&\frac {\displaystyle X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+\frac {X_{l}}{2}}{E_{\mathrm {G}}E_{\mathrm {0}}}P_{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \sin \delta ≈ \delta \ \)としてよいので,
\[
\begin{eqnarray}
\delta _{\mathrm {0}}&≈&\frac {\displaystyle X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+\frac {X_{l}}{2}}{E_{\mathrm {G}}E_{\mathrm {0}}}P_{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ P_{\mathrm {G}} =P_{\mathrm {G0}} \ \)に注意して各値を代入すると,
\[
\begin{eqnarray}
\delta _{\mathrm {0}}&=&\frac {\displaystyle 0.15+0.10+\frac {0.20}{2}}{1.0\times 1.0}\times 0.8 \\[ 5pt ]
&=&0.28 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ 1 \ \)回線開放後の不安定平衡点における位相角\( \ \delta _{\mathrm {u}} \ \mathrm {[rad]} \ \)
\( \ 1 \ \)回線開放後の同期発電機から無限大母線までのリアクタンス\( \ X^{\prime } \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
X^{\prime }&=&X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+X_{l} \\[ 5pt ]
\end{eqnarray}
\]
であり,(2)と同様に安定平衡点における位相角\( \ \delta _{\mathrm {s}} \ \mathrm {[rad]} \ \)は,
\[
\begin{eqnarray}
\delta _{\mathrm {s}}&≈&\frac {\displaystyle X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+X_{l}}{E_{\mathrm {G}}E_{\mathrm {0}}}P_{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
\delta _{\mathrm {s}}&=&\frac {\displaystyle 0.15+0.10+0.20}{1.0\times 1.0}\times 0.8 \\[ 5pt ]
&=&0.36 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,不安定平衡点における位相角\( \ \delta _{\mathrm {u}} \ \mathrm {[rad]} \ \)は,
\[
\begin{eqnarray}
\delta _{\mathrm {u}}&=&\pi – \delta _{\mathrm {s}} \\[ 5pt ]
&=&3.14 – 0.36 \\[ 5pt ]
&=&2.78 → 2.8 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \cos \delta _{\mathrm {c}} \ \)の値
図3の(A)より,加速エネルギー\( \ W_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,故障継続中の同期発電機の発電出力が\( \ P_{\mathrm {G}}=0 \ \mathrm {[p.u.]} \ \)であることから,
\[
\begin{eqnarray}
W_{\mathrm {a}}&=&\left( P_{\mathrm {G0}}-P_{\mathrm {G}} \right) \left( \delta _{\mathrm {c}} -\delta _{\mathrm {0}} \right) \\[ 5pt ]
&=&\left( 0.8-0 \right) \left( \delta _{\mathrm {c}} -0.28 \right) \\[ 5pt ]
&=&0.8 \delta _{\mathrm {c}} -0.224 \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,図3の(B)より,減速エネルギー\( \ W_{\mathrm {d}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&\int _{\delta _{\mathrm {c}}}^{\delta _{\mathrm {u}}}\left( P_{\mathrm {G}}-P_{\mathrm {G0}} \right) \mathrm {d}\delta \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.同期発電機の出力」の通り,発電出力\( \ P_{\mathrm {G}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {G}}&=&\frac {E_{\mathrm {G}}E_{\mathrm {0}}}{X^{\prime }}\sin \delta \\[ 5pt ]
&=&\frac {E_{\mathrm {G}}E_{\mathrm {0}}}{\displaystyle X_{\mathrm {d}}^{\prime }+X_{\mathrm {t}}+X_{l}}\sin \delta \\[ 5pt ]
&=&\frac {1.0\times 1.0}{\displaystyle 0.15+0.10+0.20}\sin \delta \\[ 5pt ]
&≒&2.222\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&\int _{\delta _{\mathrm {c}}}^{\delta _{\mathrm {u}}}\left( P_{\mathrm {G}}-P_{\mathrm {G0}} \right) \mathrm {d}\delta \\[ 5pt ]
&=&\int _{\delta _{\mathrm {c}}}^{\delta _{\mathrm {u}}}\left( 2.222\sin \delta -0.8 \right) \mathrm {d}\delta \\[ 5pt ]
&=&\left[ -2.222\cos \delta -0.8\delta \right] _{\delta _{\mathrm {c}}}^{\delta _{\mathrm {u}}} \\[ 5pt ]
&=& -2.222\cos \delta _{\mathrm {u}} -0.8\delta _{\mathrm {u}}+ 2.222\cos \delta _{\mathrm {c}} +0.8\delta _{\mathrm {c}} \\[ 5pt ]
&=& -2.222\cos \delta _{\mathrm {u}} -0.8\times 2.78+ 2.222\cos \delta _{\mathrm {c}} +0.8\delta _{\mathrm {c}} \\[ 5pt ]
&=& -2.222\cos \delta _{\mathrm {u}} -2.224+ 2.222\cos \delta _{\mathrm {c}} +0.8\delta _{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ W_{\mathrm {a}}=W_{\mathrm {d}} \ \)であるから,
\[
\begin{eqnarray}
0.8 \delta _{\mathrm {c}} -0.224 &=&-2.222\cos \delta _{\mathrm {u}} -2.224+ 2.222\cos \delta _{\mathrm {c}} +0.8\delta _{\mathrm {c}} \\[ 5pt ]
0 &=&-2.222\cos \delta _{\mathrm {u}} -2+ 2.222\cos \delta _{\mathrm {c}} \\[ 5pt ]
2.222\cos \delta _{\mathrm {c}} &=&2.222\cos \delta _{\mathrm {u}} +2 \\[ 5pt ]
\cos \delta _{\mathrm {c}} &≒&\cos \delta _{\mathrm {u}} +0.9001 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \delta _{\mathrm {u}}>\frac {\pi }{2} \ \)であることに注意して\( \ \cos \delta _{\mathrm {u}} \ \)を求めると,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {u}} &=&-\sqrt {1-\sin ^{2}\delta _{\mathrm {u}}} \\[ 5pt ]
&=&-\sqrt {1-\sin ^{2}\delta _{\mathrm {s}}} \\[ 5pt ]
&≈&-\sqrt {1- \delta _{\mathrm {s}}^{2}} \\[ 5pt ]
&=&-\sqrt {1- 0.36^{2}} \\[ 5pt ]
&≒&-0.9330 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {c}} &=&\cos \delta _{\mathrm {u}} +0.9001 \\[ 5pt ]
&=&-0.9330+0.9001 \\[ 5pt ]
&≒&-0.033 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは