【問題】
【難易度】★★★★☆(やや難しい)
電力系統における無効電力の変化による電圧変動に関し,次の問に答えよ。なお,各要素と単位は次のとおりとする。
有効電力\( \ P \ \):\( \ \mathrm {[W]} \ \),無効電力\( \ Q \ \):\( \ \mathrm {[var]} \ \),送電端電圧\( \ V_{\mathrm {s}} \ \)及び受電端電圧\( \ V_{\mathrm {r}} \ \):\( \ \mathrm {[V]} \ \),抵抗\( \ r \ \)及びリアクタンス\( \ x \ \):\( \ \mathrm {[\Omega ]} \ \)
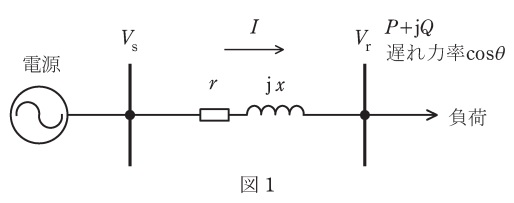
(1) 図1は,電源から負荷(遅れ力率)に電力\( \ P+\mathrm {j}Q \ \)を送電している状態を示している。次のa)及びb)について答えよ。
a) 受電端電圧\( \ V_{\mathrm {r}} \ \)を基準として,\( \ 1 \ \)相分の電圧,電流の関係をベクトル図で表せ。ただし,受電端電圧\( \ V_{\mathrm {r}} \ \)及び送電端電圧\( \ V_{\mathrm {s}} \ \)は線間電圧とする。
b) 負荷の有効電力\( \ P \ \),抵抗\( \ r \ \)及びリアクタンス\( \ x \ \)は一定とし,\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)の位相差は近似的に零であるとみなした場合,無効電力の変化\( \ \Delta Q \ \)と,それによる受電端電圧の変化\( \ \Delta v \ \)とは,①式の関係があることを証明せよ。ただし,送電端電圧\( \ V_{\mathrm {s}} \ \)は一定とし,受電端電圧\( \ V_{\mathrm {r}} \ \)の変化は小さく,また,\( \ r≪x \ \)とする。
\[
\begin{eqnarray}
\Delta v &∝& -x\cdot \Delta Q ・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
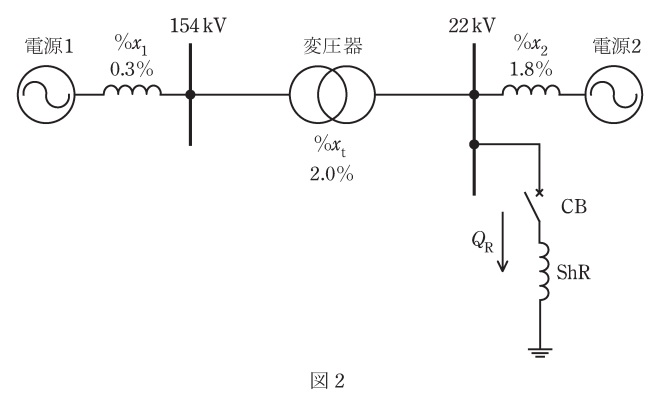
(2) 図2は,電源\( \ 1 \ \)(商用電源)に電源\( \ 2 \ \)(分散電源)が接続された電力系統を示している。\( \ 22 \ \mathrm {kV} \ \)母線に分路リアクトル(\( \ \mathrm {ShR} \ \)を投入したとき,\( \ 22 \ \mathrm {kV} \ \)母線の電圧変動率を\( \ 2 \ \)%以下にするためには,投入する容量\( \ Q_{\mathrm {R}} \ \)は最大何\( \ \mathrm {Mvar} \ \)とすべきか。\( \ 1 \ \mathrm {Mvar} \ \)未満は四捨五入して答えよ。ただし,①式が成立するものとし,\( \ 22 \ \mathrm {kV} \ \)母線の電圧\( \ V_{22} \ \)の送電端電圧\( \ V_{\mathrm {s}} \ \)に対する電圧変化を\( \ v \ \)とすると,\( \ 22 \ \mathrm {kV} \ \)母線の電圧変動率\( \ %v_{22} \ \)は次式で表されるものとする。
\[
\begin{eqnarray}
%v_{22}[%] &=& \frac {v}{V_{22}} \times 100 \ [%]\\[ 5pt ]
\end{eqnarray}
\]
また,系統各部のリアクタンスは\( \ 10 \ \mathrm {MV\cdot A} \ \)基準の値とし,電源電圧は変化しないものとする。
【ワンポイント解説】
ベクトル図の作図とそれを使用した計算,百分率インピーダンス等2種の二次試験として非常によく出題される内容のオンパレードといった問題です。「受電端電圧\( \ V_{\mathrm {r}} \ \)及び送電端電圧\( \ V_{\mathrm {s}} \ \)は線間電圧とする。」という条件を忘れると大幅に減点されると予想されます。十分に注意しましょう。
1.百分率インピーダンス
基準容量を\(P_{\mathrm {B}}\),基準電圧を\(V_{\mathrm {B}}\)とすると,
\[
\begin{eqnarray}
%P&=&\frac {P \ \mathrm {[W]}}{P_{\mathrm {B}}}\times 100 \\[ 5pt ]
%V&=&\frac {V \ \mathrm {[V]}}{V_{\mathrm {B}}}\times 100 \\[ 5pt ]
%I&=&\frac {I \ \mathrm {[A]}}{I_{\mathrm {B}}}\times 100 \\[ 5pt ]
&=&\frac {I \ \mathrm {[A]}}{\displaystyle \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}V_{\mathrm {B}}}{P_{\mathrm {B}}}\cdot I \ \mathrm {[A]}\times 100 \\[ 5pt ]
%Z&=&\frac {Z \ \mathrm {[\Omega ]}}{Z_{\mathrm {B}}}\times 100 \\[ 5pt ]
&=&\frac {Z \ \mathrm {[\Omega ]}}{\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}I_{\mathrm {B}}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}}I_{\mathrm {B}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}} \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となります。最後の\(%Z\)の式は公式として暗記しておきましょう。
【関連する「電気の神髄」記事】
【解答】
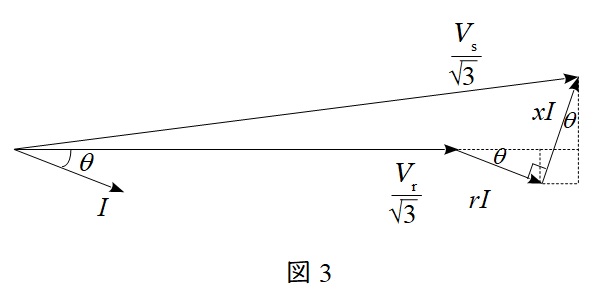
(1)a)\( \ V_{\mathrm {r}} \ \)を基準とした時の\( \ 1 \ \)相分の電圧,電流の関係をベクトル図
負荷が遅れ力率であるので,電流は電圧より遅れとなり,抵抗での電圧降下\( \ rI \ \)は電流と同相,リアクタンスでの電圧降下は電流より\( \ \displaystyle \frac {\pi }{2} \ \)進みとなる。したがって,ベクトル図は図3のようになる。
(1)b) \( \ \Delta v ∝ -x\cdot \Delta Q \ \)の証明
\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)の位相差は近似的に零であるので,図3より,
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&=&\frac {V_{\mathrm {r}}}{\sqrt {3}}+rI\cos \theta +xI\sin \theta \\[ 5pt ]
\frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&rI\cos \theta +xI\sin \theta \\[ 5pt ]
V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( rI\cos \theta +xI\sin \theta \right) \\[ 5pt ]
V_{\mathrm {r}}&=&V_{\mathrm {s}}-\sqrt {3}\left( rI\cos \theta +xI\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで有効電力\( \ P \ \)と無効電力\( \ Q \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3}V_{\mathrm {r}}I\cos \theta \\[ 5pt ]
I\cos \theta &=&\frac {P}{\sqrt {3}V_{\mathrm {r}}} \\[ 5pt ]
Q&=&\sqrt {3}V_{\mathrm {r}}I\sin \theta \\[ 5pt ]
I\sin \theta &=&\frac {Q}{\sqrt {3}V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&V_{\mathrm {s}}-\sqrt {3}\left( rI\cos \theta +xI\sin \theta \right) \\[ 5pt ]
&=&V_{\mathrm {s}}-\sqrt {3}\left( \frac {rP}{\sqrt {3}V_{\mathrm {r}}} +\frac {xQ}{\sqrt {3}V_{\mathrm {r}}} \right) \\[ 5pt ]
&=&V_{\mathrm {s}}-\frac {rP+xQ}{V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ r≪x \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&V_{\mathrm {s}}-\frac {rP+xQ}{V_{\mathrm {r}}} \\[ 5pt ]
&≃&V_{\mathrm {s}}-\frac {xQ}{V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ V_{\mathrm {s}} \ \)は一定であるので,受電端電圧の変化\( \ \Delta v \ \)は,
\[
\begin{eqnarray}
\Delta v &=&-\frac {x\cdot \Delta Q}{V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
の関係となる。したがって,\( \ \Delta v ∝ -x\cdot \Delta Q \ \)の関係が成立する。
(2)電圧変動率を\( \ 2 \ \)%以下にするためには,投入する容量\( \ Q_{\mathrm {R}} \ \)の最大値
\( \ 22 \ \mathrm {kV} \ \)母線から電源側を見た合成リアクタンス\( \ %x \ \)は,
\[
\begin{eqnarray}
%x &=&\frac {\left( %x_{1}+%x_{\mathrm {t}}\right) \cdot %x_{2}}{\left( %x_{1}+%x_{\mathrm {t}}\right) + %x_{2}} \\[ 5pt ]
&=&\frac {\left( 0.3+2.0\right) \times 1.8}{\left( 0.3+2.0\right) + 1.8} \\[ 5pt ]
&≒&1.0098 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.百分率インピーダンス」の通り,
\[
\begin{eqnarray}
%x&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot x\times 100 \\[ 5pt ]
x&=&\frac {V_{\mathrm {B}}^{2}}{P_{\mathrm {B}}\times 100 }\cdot %x\\[ 5pt ]
&=&\frac {\left( 22\times 10^{3}\right) ^{2}}{10\times 10^{6}\times 100 }\times 1.0098 \\[ 5pt ]
&≒&0.48874 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。また,(1)b)の解答式より,\( \ V_{\mathrm {s}}≒V_{\mathrm {r}} \ \)であることに注意すると,
\[
\begin{eqnarray}
\left| v\right| &=&\frac {x\cdot Q_{\mathrm {R}}}{V_{\mathrm {22}}} \\[ 5pt ]
Q_{\mathrm {R}}&=&\frac {\left| v\right| V_{\mathrm {22}}}{x} \\[ 5pt ]
\end{eqnarray}
\]
となる。電圧変動率の定義式より,
\[
\begin{eqnarray}
%v_{22}[%] &=& \frac {v}{V_{22}} \times 100 \ [%]\\[ 5pt ]
2&=& \frac {v}{22\times 10^{3}} \times 100 \\[ 5pt ]
v&=&440 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを代入すると,
\[
\begin{eqnarray}
Q_{\mathrm {R}}&=&\frac {\left| v\right| V_{\mathrm {22}}}{x} \\[ 5pt ]
&=&\frac {440\times 22\times 10^{3}}{0.48874} \\[ 5pt ]
&≒&19806000 \ \mathrm {[var]} → 19.806 \ \mathrm {[Mvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。小数点以下を四捨五入すると\( \ 20 \ \mathrm {[Mvar]} \ \)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは