《電力》〈送電〉[R05:問4]電力系統の短絡容量とインピーダンスに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電力系統の短絡容量と，この計算に関係するインピーダンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

地点$ \ \mathrm {S} \ $の短絡容量$ \ W_{\mathrm {S}} \ \mathrm {[MV\cdot A]} \ $は，同地点の単位法の基準電圧(定格電圧)を$ \ V_{\mathrm {S}} \ \mathrm {[kV]} \ $，$ \ 3 \ $相短絡電流を$ \ I_{\mathrm {S}} \ \mathrm {[kA]} \ $とするとき，次式で定義される。
\[
\begin{eqnarray}
W_{\mathrm {S}} &=& \sqrt {3}V_{\mathrm {S}}\times I_{\mathrm {S}} \\[ 5pt ] \end{eqnarray}
\] 上式は，短絡地点$ \ \mathrm {S} \ $$ \ \fbox {　（１）　} \ $正相インピーダンスの大きさを$ \ Z_{\mathrm {S}} \ \mathrm {[p.u.]} \ $，単位法の系統基準容量を$ \ W_{\mathrm {base}} \ \mathrm {[MV\cdot A]} \ $とするとき，次式で記述できる。
\[
\begin{eqnarray}
W_{\mathrm {S}} &=& \ \fbox {　（２）　} \ \\[ 5pt ] \end{eqnarray}
\] $ \ Z_{\mathrm {S}} \ $は，複数母線系統では，一般に$ \ \fbox {　（３）　} \ $の駆動点インピーダンス要素として得られる。この$ \ Z_{\mathrm {S}} \ $は，系統規模が大きく，また系統が$ \ \fbox {　（４）　} \ $であるほど小さいため，そうした系統では短絡容量は大きくなる。これらの特徴から，短絡容量の大小はその地点近傍の$ \ \fbox {　（５）　} \ $能力を表す目安としても用いられる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　から系統を見た　　　　　　　&（ロ）&　\frac {W_{\mathrm {base}}}{Z_{\mathrm {S}}}　　　　　&（ハ）&　樹枝状 \\[ 5pt ] &（ニ）&　電圧維持　　　　　&（ホ）&　\frac {W_{\mathrm {base}}}{\sqrt {3}Z_{\mathrm {S}}}　　　　　&（ヘ）&　ノードインピーダンス行列 \\[ 5pt ] &（ト）&　に接続する　　　　　&（チ）&　ヤコビ行列　　　　　&（リ）&　と発電機母線間の \\[ 5pt ] &（ヌ）&　電力変動抑制　　　　　&（ル）&　放射状　　　　　&（ヲ）&　発電電力制御 \\[ 5pt ] &（ワ）&　短絡特性行列　　　　　&（カ）&　\frac {\sqrt {3}W_{\mathrm {base}}}{Z_{\mathrm {S}}}　　　　　&（ヨ）&　メッシュ状 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電力系統の潮流短絡計算の中身に関する出題です。
$ \ 2 \ $種では二次試験で計算問題が出題されるため，本問のような内容でも一次試験では知識問題が出題されます。
一次試験と二次試験はしっかりと分けて対策するようにしましょう。

1.三相短絡事故時の短絡電流及び短絡容量
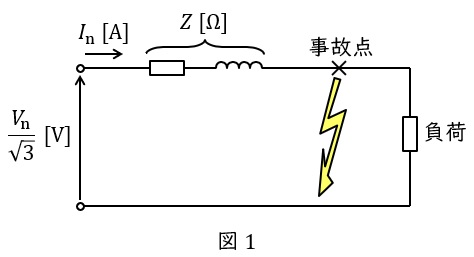
図1のような負荷に定格電圧$ \ V_{\mathrm {n}} \ \mathrm {[V]} \ $，定格電流$ \ I_{\mathrm {n}} \ \mathrm {[A]} \ $で供給している系統があり，事故点において三相短絡事故が発生したとします。
事故点から電源側をみたインピーダンスを$ \ Z \ \mathrm {[\Omega ]} \ $とすると，その単位法におけるインピーダンス$ \ Z \ \mathrm {[p.u.]} \ $は，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]}&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]}I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}
\] とで定義され，図1より三相短絡電流$ \ I_{\mathrm {s}} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\cdot I_{\mathrm {n}} \\[ 5pt ] &=&\frac {I_{\mathrm {n}}}{Z \ \mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}
\] となります。また，短絡容量$ \ P_{\mathrm {s}} \ \mathrm {[V\cdot A]} \ $は，定格容量$ \ P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ $とおくと，
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\sqrt {3}V_{\mathrm {n}}I_{\mathrm {s}} \\[ 5pt ] &=&\frac {\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}}}{Z \ \mathrm {[p.u.]}}\\[ 5pt ] &=&\frac {P_{\mathrm {n}}}{Z \ \mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，短絡電流及び短絡容量の抑制対策としては，系統のインピーダンスを大きくする方法が有効であることがわかります。

【解答】

(1)解答：イ
題意より解答候補は，（イ）から系統を見た，（ト）に接続する，（リ）と発電機母線間の，になると思います。
ワンポイント解説「1.三相短絡事故時の短絡電流及び短絡容量」の通り，事故電流を考えるときは，短絡地点から系統を見た正相インピーダンスを使用します。

(2)解答：ロ
題意より解答候補は，（ロ）$ \ \displaystyle \frac {W_{\mathrm {base}}}{Z_{\mathrm {S}}} \ $，（ホ）$ \ \displaystyle\frac {W_{\mathrm {base}}}{\sqrt {3}Z_{\mathrm {S}}} \ $，（カ）$ \ \displaystyle\frac {\sqrt {3}W_{\mathrm {base}}}{Z_{\mathrm {S}}} \ $，になると思います。
ワンポイント解説「1.三相短絡事故時の短絡電流及び短絡容量」の通り，$ \ W_{\mathrm {S}} \ \mathrm {[MV\cdot A]} \ $は，
\[
\begin{eqnarray}
W_{\mathrm {S}} &=&\frac {W_{\mathrm {base}}}{Z_{\mathrm {S}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

(3)解答：ヘ
題意より解答候補は，（ヘ）ノードインピーダンス行列，（チ）ヤコビ行列，（ワ）短絡特性行列，等になると思います。
複数母線系統において，ノード電圧（ノードとは発電機、負荷等の接続点のことをいいます）$ \ \displaystyle \dot {\boldsymbol V}=\left(
\begin{array}{c}
{\dot V}_{ 1 } \\
{\dot V}_{ 2 } \\
\vdots \\
{\dot V}_{ n }
\end{array}
\right) \ $，ノード電流$ \ \displaystyle \dot {\boldsymbol I}=\left(
\begin{array}{c}
{\dot I}_{ 1 } \\
{\dot I}_{ 2 } \\
\vdots \\
{\dot I}_{ n }
\end{array}
\right) \ $とすると，
\[
\begin{eqnarray}
\left(
\begin{array}{c}
{\dot V}_{ 1 } \\
{\dot V}_{ 2 } \\
\vdots \\
{\dot V}_{ n }
\end{array}
\right) =
\left(
\begin{array}{cccc}
{\dot Z}_{ 11 } & {\dot Z}_{ 12 } & \ldots & {\dot Z}_{ 1n } \\
{\dot Z}_{ 21 } & {\dot Z}_{ 22 } & \ldots & {\dot Z}_{ 2n } \\
\vdots & \vdots & \ddots & \vdots \\
{\dot Z}_{ n1 } & {\dot Z}_{ n2 } & \ldots & {\dot Z}_{ nn }
\end{array}
\right)
\left(
\begin{array}{c}
{\dot I}_{ 1 } \\
{\dot I}_{ 2 } \\
\vdots \\
{\dot I}_{ n }
\end{array}
\right)
\end{eqnarray}
\] の関係があり，$ \ \displaystyle \dot {\boldsymbol Z}=\left(
\begin{array}{cccc}
{\dot Z}_{ 11 } & {\dot Z}_{ 12 } & \ldots & {\dot Z}_{ 1n } \\
{\dot Z}_{ 21 } & {\dot Z}_{ 22 } & \ldots & {\dot Z}_{ 2n } \\
\vdots & \vdots & \ddots & \vdots \\
{\dot Z}_{ n1 } & {\dot Z}_{ n2 } & \ldots & {\dot Z}_{ nn }
\end{array}
\right) \ $をノードインピーダンス行列といいます。

(4)解答：ヨ
題意より解答候補は，（ハ）樹枝状，（ル）放射状，（ヨ）メッシュ状，になると思います。
短絡地点$ \ \mathrm {S} \ $から系統を見た正相インピーダンスの大きさ$ \ Z_{\mathrm {S}} \ \mathrm {[p.u.]} \ $はメッシュ状になると小さくなります。電気回路で並列合成インピーダンスが小さくなるのと同じです。

(5)解答：ニ
題意より解答候補は，（ニ）電圧維持，（ヌ）電力変動抑制，（ヲ）発電電力制御，になると思います。
問題文の通り$ \ Z_{\mathrm {S}} \ \mathrm {[p.u.]} \ $は短絡容量と関係があり，$ \ Z_{\mathrm {S}} \ \mathrm {[p.u.]} \ $はその地点での電圧変動に影響するため，短絡容量の大小は電圧維持能力を表す目安にもなります。