《機械》〈変圧器〉[H21:問2]変圧器の損失の種類と効率に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，二巻線変圧器の損失と効率とに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句又は式を解答群の中から選び，その記号をマークシートに記入しなさい。

変圧器の損失には，無負荷損と負荷損とがある。

無負荷損は，一方の巻線を開路し，他方の巻線に定格周波数の電圧を加えたときに消費される有効電力である。無負荷損は，そのほとんどが$ \ \fbox {　（１）　} \ $である。

負荷損は，一方の巻線を短絡し，他方の巻線に定格周波数の電圧を加えて電流を通じたときに消費される有効電力であり，$ \ \fbox {　（２）　} \ $巻線温度における値に補正して表す。

変圧器の効率$ \ \eta \ $は，定格二次電圧及び定格周波数における出力，並びに全損失を用いて次式で求められる値で表す。これを$ \ \fbox {　（３）　} \ $効率という。ここで全損失とは，無負荷損と負荷損との和である。
\[
\begin{eqnarray}
\eta &=&\frac {出力 \ \mathrm {[W]}}{出力 \ \mathrm {[W]} \ +全損失 \ \mathrm {[W]}}\times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] 定格容量$ \ S_{n} \ \mathrm {[V\cdot A]} \ $の変圧器がある。その定格電圧における無負荷損は$ \ P_{i} \ \mathrm {[W]} \ $，定格電流を通じたときの負荷損は$ \ P_{c} \ \mathrm {[W]} \ $である。力率が$ \ \cos \phi \ $の負荷を二次端子に接続し，定格二次電圧及び定格周波数としてこの変圧器を負荷率（負荷の容量の変圧器定格容量に対する比）$ \ m \ \mathrm {[p.u.]} \ $で用いたときの効率$ \ \eta \ $は，次式となる。
\[
\begin{eqnarray}
\eta &=&\frac { \ \fbox {　（４）　} \ }{ \ \fbox {　（４）　} \ +P_{i}+ \ \fbox {　（５）　} \ }\times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\]

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　実　測　　　　　&（ロ）&　規　約　　　　　&（ハ）&　鉄　損 \\[ 5pt ] &（ニ）&　m\cdot p_{c}　　　　　&（ホ）&　漂遊負荷損　　　　　&（ヘ）&　\left( m\cdot \cos \phi \right) ^{2}\cdot P_{c} \\[ 5pt ] &（ト）&　理　論　　　　　&（チ）&　m\cdot S_{n}\cdot \cos \phi 　　　　　&（リ）&　定　格 \\[ 5pt ] &（ヌ）&　m^{2}\cdot P_{c}　　　　&（ル）&　銅　損　　　　　&（ヲ）&　m^{2}\cdot S_{n} \\[ 5pt ] &（ワ）&　\left( m\cdot \cos \phi \right) ^{2}\cdot S_{n}　　　　　&（カ）&　最　高　　　　　&（ヨ）&　基　準 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

変圧器の損失と効率に関する問題です。
(2)の空欄だけ少し迷う受験生もいると考えられるため★２としましたが，それ以外の空欄は正答しておきたい内容となります。その他，もう少し細かい区分けとして変圧器の無負荷損（鉄損）にはヒステリシス損や渦電流損，負荷損には銅損や漂遊負荷損があることを覚えておいて下さい。

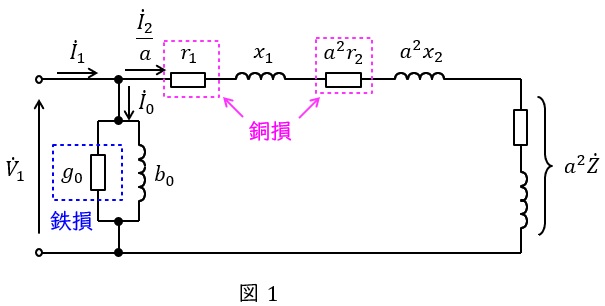
1.変圧器の等価回路（一次換算）と鉄損及び銅損
変圧器の一次側換算等価回路を図1に示します。ただし，$ \ {\dot V}_{1} \ \mathrm {[V]} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ \mathrm {[A]} \ $は一次電流，$ \ {\dot I}_{2} \ \mathrm {[A]} \ $は二次電流，$ \ {\dot I}_{0} \ \mathrm {[A]} \ $は励磁電流，$ \ r_{1} \ \mathrm {[\Omega ]} \ $は一次巻線抵抗，$ \ r_{2} \ \mathrm {[\Omega ]} \ $は二次巻線抵抗，$ \ x_{1} \ \mathrm {[\Omega ]} \ $は一次漏れリアクタンス，$ \ x_{2} \ \mathrm {[\Omega ]} \ $は二次漏れリアクタンス，$ \ g_{0} \ \mathrm {[S]} \ $は励磁コンダクタンス，$ \ b_{0} \ \mathrm {[S]} \ $は励磁サセプタンス，$ \ a \ $は変圧比（巻数比）となります。
等価回路より，鉄損は電圧$ \ {\dot V}_{1} \ $の$ \ 2 \ $乗に比例し，銅損は電流$ \ {\dot I}_{2} \ $の$ \ 2 \ $乗に比例することがわかります。

2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $
変圧器の損失は主に鉄損$ \ p_{\mathrm {i}} \ \mathrm {[W]} \ $と銅損$ \ p_{\mathrm {c}} \ \mathrm {[W]} \ $があり，$ \ p_{\mathrm {i}} \ \mathrm {[W]} \ $は負荷によらず一定であり，$ \ p_{\mathrm {c}} \ \mathrm {[W]} \ $は負荷(電流)の$ \ 2 \ $乗に比例します。従って，定格出力$ \ P_{\mathrm {n}} \ \mathrm {[W]} \ $で利用率$ \ \alpha \ $の時の変圧器の効率$ \ \eta \ $は，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ] &=&\frac {出力}{出力+損失} \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となります。
次に，最大効率$ \ \eta _{\mathrm {m}} \ $を求めます。上式の分母分子を$ \ \alpha \ $で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となり，効率が最大となるためには，上式の分母が最小となれば良いです。よって，$ \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ $と置くと，
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となります。よって$ \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ $となるとき，$ \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ $であり，鉄損と銅損が等しい時効率は最大となります。

3.実測効率と規約効率
一般に効率は$ \ \displaystyle \frac {出力}{入力}\times 100 \ \mathrm {[％]} \ $で求められます。

①実測効率
実測効率は機器に実負荷をかけて入力と出力を測定し，効率を求めるものです。
しかしながら，大容量機（器）では実際に定格負荷をかけることが困難であったり，発電機や電動機のような入出力の一方が機械的な入出力である場合等は正確な測定が困難である場合があります。

②規約効率
大容量機（器）等実測効率を適用することが困難な場合には，規定された方法で入力もしくは出力と損失を測定し効率を算出します。
規約効率での効率は，$ \ \displaystyle \frac {出力}{出力＋損失}\times 100 \ \mathrm {[％]} \ $もしくは$ \ \displaystyle \frac {入力－損失}{入力}\times 100 \ \mathrm {[％]} \ $で求められます。

【解答】

(1)解答：ハ
題意より解答候補は，（ハ）鉄損，（ホ）漂遊負荷損，（ル）銅損，になると思います。
変圧器の無負荷損はそのほとんどが鉄損となります。漂遊負荷損及び銅損は共に負荷損となります。

(2)解答：ヨ
題意より解答候補は，（イ）実測，（ロ）規約，（ト）理論，（リ）定格，（カ）最高，（ヨ）基準，になると思います。
負荷損は温度により変化するため，基準巻線温度における値に補正します。電験では出題される可能性は少ないかもしれませんが，変圧器の基準巻線温度は$ \ 75 \ \mathrm {[℃]} \ $であることは覚えておいても良いかと思います。

(3)解答：ロ
題意より解答候補は，（イ）実測，（ロ）規約，（ト）理論，（リ）定格，（カ）最高，（ヨ）基準，になると思います。
ワンポイント解説「3.実測効率と規約効率」の通り，定格二次電圧及び定格周波数における出力，並びに全損失を用いて求める効率を規約効率といいます。

(4)解答：チ
題意より解答候補は，（チ）$ \ m\cdot S_{n}\cdot \cos \phi \ $，（ヲ）$ \ m^{2}\cdot S_{n} \ $，（ワ）$ \ \left( m\cdot \cos \phi \right) ^{2}\cdot S_{n} \ $，になると思います。
ワンポイント解説「2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $」の通り，負荷率$ \ m \ \mathrm {[p.u.]} \ $の変圧器の出力は有効電力が$ \ S_{n}\cdot \cos \phi \ $なので$ \ m\cdot S_{n}\cdot \cos \phi \ $となります。

(5)解答：ヌ
題意より解答候補は，（ニ）$ \ m\cdot p_{c} \ $，（ヘ）$ \ \left( m\cdot \cos \phi \right) ^{2}\cdot P_{c} \ $，（ヌ）$ \ m^{2}\cdot P_{c} \ $，になると思います。
ワンポイント解説「2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $」の通り，銅損は負荷容量の$ \ 2 \ $乗に比例するため，負荷率$ \ m \ \mathrm {[p.u.]} \ $の変圧器の銅損は$ \ m^{2}\cdot P_{c} \ $となります。