Contents
【問題】
【難易度】★★★☆☆(普通)
定格電圧,一定出力のもとで運転している非突極形三相同期電動機がある。界磁電流\( \ I_{f} \ \)を調整して\( \ I_{f0} \ \)としたところ,入力電流が\( \ 0.5 \ \mathrm {[p.u.]} \ \),力率\( \ 1 \ \)となった。次の問に答えよ。ただし,短絡比は\( \ 0.8 \ \)であり,電機子抵抗,機械損及び鉄心の磁気飽和は無視できるものとする。
(1) 自己容量基準の単位法で表した無負荷誘導起電力\( \ E_{0} \ \)及び出力\( \ P \ \)を求めよ。
(2) 一定出力を維持できる界磁電流の範囲で,\( \ I_{f} \ \)を変化させても,負荷角を\( \ δ \ \)とするとき\( \ E_{0}\sin \delta \ \)が一定であることを示し,その値(単位法)を求めよ。
(3) 界磁電流\( \ I_{f} \ \)を\( \ kI_{f0} \ \)に設定した。このときの無負荷誘導起電力を\( \ E_{01} \ \),負荷角を\( \ \delta _{1} \ \)とする。
\( \ \mathrm {a.} \ \)端子電圧\( \ \dot V \ \)を基準ベクトル(フェーザ)とするとき,\( \ E_{01} \ \)及び\( \ δ_{1} \ \)を用いて入力電流\( \ {\dot I}_{a1} \ \)を表す式を求めよ。
\( \ \mathrm {b.} \ \)\( \ k = 1.5 \ \)に調整したときの無負荷誘導起電力\( \ E_{01} \ \)(単位法)を求めよ。
\( \ \mathrm {c.} \ \)\( \ k = 1.5 \ \)に調整したときの入力電流\( \ I_{a1} \ \)の大きさ(単位法)及び力率を求めよ。また,力率は遅れ又は進みのどちらか。
【ワンポイント解説】
単位法を用いた三相同期電動機の諸計算を行う問題です。
ベクトル図を描いて解いていき,計算量も比較的多い問題なので,\( \ 30 \ \)分で解くには少し厳しい問題であったかもしれません。
ただし,いずれの設問も同期機として重要な内容ばかりなので,練習問題としてはとても良い問題かと思います。
1.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は,端子電圧\( \ \dot V \ \mathrm {[V]} \ \)(相電圧),誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)(相電圧),電機子電流\( \ \dot I \ \mathrm {[A]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると,図1のようになります。ただし,電機子巻線抵抗は十分に小さいものとします。
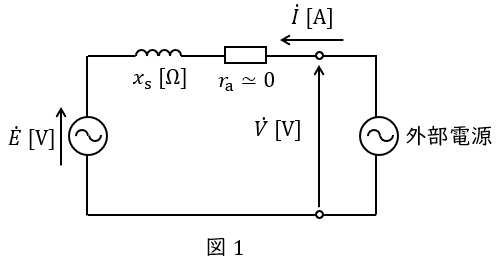
等価回路にキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
これより,\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \),\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot E \ \mathrm {[V]} \ \)の負荷角を\( \ \delta \ \mathrm {[rad]} \ \)とすると,ベクトル図は図2のように描くことができます。
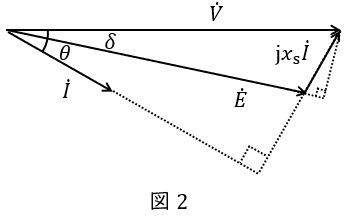
2.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)
図3のベクトル図に示すように,端子電圧\( \ \dot V \ \mathrm {[V]} \ \)(相電圧),誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)(相電圧),電機子電流\( \ \dot I \ \mathrm {[A]} \ \),\( \ \dot E \ \)と\( \ \dot V \ \)の位相差(負荷角)を\( \ \delta \ \mathrm {[rad]} \ \),\( \ \dot V \ \)と\( \ \dot I \ \)の位相差(力率角)を\( \ \theta \ \mathrm {[rad]} \ \)とすると,出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ]
\end{eqnarray}
\]
で求められ,図3の※線を求める式より,
\[
\begin{eqnarray}
x_{\mathrm {s}}I\cos \left( \theta -\delta \right) &=&V\sin \delta \\[ 5pt ]
I\cos \left( \theta -\delta \right) &=&\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ]
&=&3E\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
&=&\frac {3VE}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
と求められます。最後の式は公式として覚えておくと良いでしょう。
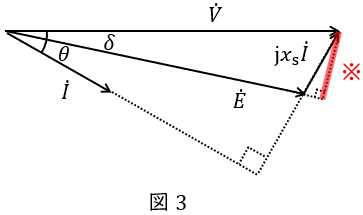
3.単位法における電力
誘導起電力(相電圧)\( \ {\dot E} \ \mathrm {[V]} \ \),端子電圧(相電圧)\( \ \dot V \ \mathrm {[V]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),相電流\( \ \dot I \ \mathrm {[A]} \ \)とし,電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)が無視でき,力率角\( \ \theta \ \mathrm {[rad]} \ \),負荷角\( \ \delta \ \mathrm {[rad]} \ \)としたとき,同期電動機の出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3VI\cos \theta \\[ 5pt ]
&=&\frac {3EV\sin \delta }{x_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められますが,基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
\frac {P}{P_{\mathrm {n}}} &=&\frac {3VI}{3V_{\mathrm {n}}I_{\mathrm {n}}}\cos \theta \\[ 5pt ]
\frac {P}{P_{\mathrm {n}}} &=&\frac {V}{V_{\mathrm {n}}}\frac {I}{I_{\mathrm {n}}}\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&V \ \mathrm {[p.u.]}I \ \mathrm {[p.u.]}\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]} &=&\frac {E \ \mathrm {[p.u.]} \ V\ \mathrm {[p.u.]}\sin \delta }{x_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
となります。いずれも単位法で考える場合,係数の\( \ 3 \ \)がなくなることに注意しましょう。
4.同期発電機の無負荷飽和曲線と三相短絡曲線
同期発電機は図4のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷飽和曲線は定格速度で無負荷で運転したときの界磁電流と端子電圧の関係,三相短絡曲線は電機子巻線の三相の出力端子を短絡し定格速度で運転したときの界磁電流と三相短絡電流の関係,を表したものです。
図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧,\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流,無負荷飽和曲線は磁気飽和により曲線となり,三相短絡曲線は曲線ですが,ほぼ比例の直線と近似できます。
この時,\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり,短絡比\( \ K \ \)は,
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
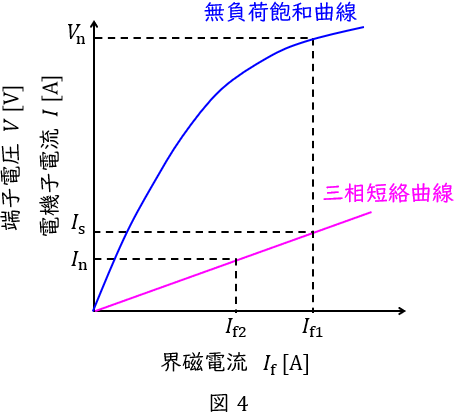
5.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の単位法で表したインピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
6.単位法で表した同期インピーダンスと短絡比の関係
同期発電機の単位法で表した同期インピーダンスが\( \ Z \ \mathrm {[p.u.]} \ \),短絡比が\( \ K \ \)であるとき,
\[
\begin{eqnarray}
K&=&\frac {1}{Z \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
※単位法の定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}} \\[ 5pt ]
\frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ]
K&=&\frac {1}{Z} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)単位法で表した無負荷誘導起電力\( \ E_{0} \ \)及び出力\( \ P \ \)
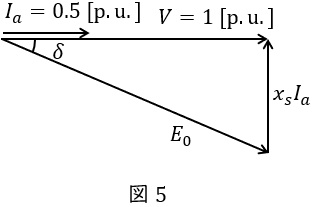
定格電圧\( \ V=1 \ \mathrm {[p.u.]} \ \)で入力電流\( \ I_{a}=0.5 \ \mathrm {[p.u.]} \ \),力率\( \ 1 \ \)となったときのベクトル図を示すと図5の通りとなる。
短絡比\( \ K=0.8 \ \)なので,同期リアクタンス\( \ x_{s} \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「6.単位法で表した同期インピーダンスと短絡比の関係」の通り,
\[
\begin{eqnarray}
x_{s}&=&\frac {1}{K} \\[ 5pt ]
&=&\frac {1}{0.8} \\[ 5pt ]
&=&1.25 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,無負荷誘導起電力\( \ E_{0} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E_{0}&=&\sqrt {V^{2}+\left( x_{s}I_{a}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {1^{2}+\left( 1.25\times 0.5\right) ^{2}} \\[ 5pt ]
&≒&1.179 \ 2 → 1.18 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,出力\( \ P \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「3.単位法における電力」の通り,
\[
\begin{eqnarray}
P&=&VI_{a} \\[ 5pt ]
&=&1\times 0.5 \\[ 5pt ]
&=&0.5 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ I_{f} \ \)を変化させても,\( \ E_{0}\sin \delta \ \)が一定であることを示し,その値
電動機の出力\( \ P \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「3.単位法における電力」の通り,
\[
\begin{eqnarray}
P&=&\frac {E_{0}V\sin \delta }{x_{s}} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ E_{0}\sin \delta \ \)について整理すると,
\[
\begin{eqnarray}
E_{0}\sin \delta &=&\frac {Px_{s}}{V} \\[ 5pt ]
\end{eqnarray}
\]
となる。右辺はすべて定数なので,\( \ E_{0}\sin \delta \ \)は一定となり,その値は,
\[
\begin{eqnarray}
E_{0}\sin \delta &=&\frac {0.5\times 1.25}{1} \\[ 5pt ]
&=&0.625 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {a.} \ \)\( \ E_{01} \ \)及び\( \ δ_{1} \ \)を用いて入力電流\( \ {\dot I}_{a1} \ \)を表す式
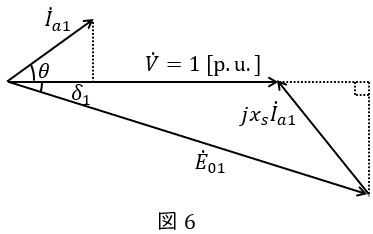
鉄心の磁気飽和を無視したとき,界磁電流と誘導起電力は比例するため,\( \ k>1 \ \)のときのベクトル図は図6の通りとなる。ベクトル図より,
\[
\begin{eqnarray}
\dot V &=&{\dot E}_{01}+ jx_{s}{\dot I}_{a1} \\[ 5pt ]
jx_{s}{\dot I}_{a1}&=&\dot V-{\dot E}_{01} \\[ 5pt ]
{\dot I}_{a1}&=&\frac {\dot V-{\dot E}_{01}}{jx_{s}} \\[ 5pt ]
&=&-j\frac {\dot V-{\dot E}_{01}}{x_{s}} \\[ 5pt ]
&=&-j\frac {V-E_{01}\left( \cos \delta_{1} -j\sin \delta_{1} \right) }{x_{s}} \\[ 5pt ]
&=&\frac {E_{01}\sin \delta_{1} +j\left( E_{01}\cos \delta_{1} -V\right) }{x_{s}} \\[ 5pt ]
&=&\frac {0.625 +j\left( E_{01}\cos \delta_{1} -1\right) }{1.25} \\[ 5pt ]
&=&0.5+j\left( 0.8E_{01}\cos \delta_{1} -0.8\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {b.} \ \)\( \ k = 1.5 \ \)に調整したときの無負荷誘導起電力\( \ E_{01} \ \)
鉄心の磁気飽和を無視したとき,界磁電流と誘導起電力は比例するため,\( \ k=1.5 \ \)のときの無負荷誘導起電力\( \ E_{01} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E_{01}&=&1.5E_{0} \\[ 5pt ]
&=&1.5\times 1.179 \ 2 \\[ 5pt ]
&=&1.768 \ 8 → 1.77 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {c.} \ \)\( \ k = 1.5 \ \)に調整したときの入力電流\( \ I_{a1} \ \)の大きさ及び力率
\( \ E_{01}\sin \delta _{1} =0.625 \ \mathrm {[p.u.]} \ \)より,\( \ \sin \delta _{1} \ \)及び\( \ \cos \delta _{1} \ \)は,
\[
\begin{eqnarray}
\sin \delta _{1} &=&\frac {0.625}{E_{01}} \\[ 5pt ]
&=&\frac {0.625}{1.768 \ 8} \\[ 5pt ]
&≒&0.353 \ 35 \\[ 5pt ]
\cos \delta _{1} &=&\sqrt {1-\sin ^{2}\delta } \\[ 5pt ]
&=&\sqrt {1-{0.353 \ 35}^{2} } \\[ 5pt ]
&≒&0.935 \ 49 \\[ 5pt ]
\end{eqnarray}
\]
となるので,(3)a.解答式より,入力電流の大きさ\( \ I_{a1} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{a1}&=&\sqrt {0.5^{2}+\left( 0.8E_{01}\cos \delta_{1} -0.8\right) ^{2}} \\[ 5pt ]
&=&\sqrt {0.5^{2}+\left( 0.8\times 1.768 \ 8\times 0.935 \ 49 -0.8\right) ^{2}} \\[ 5pt ]
&=&0.724 \ 10 → 0.724 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,力率\( \ \cos \theta \ \)は,
\[
\begin{eqnarray}
\cos \theta &=&\frac {I_{a}}{I_{a1}} \\[ 5pt ]
&=&\frac {0.5}{0.724 \ 10} \\[ 5pt ]
&=&0.691(進み) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは