《機械・制御》〈回転機〉[H29:問1]三相円筒形同期発電機に関する計算及び論述問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★☆☆☆（やや易しい）

三相円筒形同期発電機の電圧変動率，出力電流及び出力に関して，次の問に答えよ。ただし，電機子抵抗による電圧降下及び磁気飽和は無視するものとする。また，単位法は自己定格容量(定格皮相電力\( \ \mathrm{ [kV\cdot A] } \ \))を基準としている。

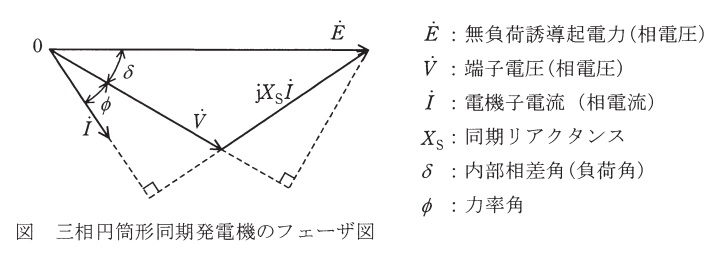
(1)　図に星形結線の\( \ 1 \ \)相分のフェーザ図を示す。その負荷状態での電圧変動率\( \ \varepsilon \ \)を\( \ \displaystyle \varepsilon =\frac {E-V}{V}\times 100 \ [％] \ \)と定義する。この\( \ \varepsilon \ \)を\( \ V \ \)，\( \ I \ \)，\( \ X_{\mathrm {S}} \ \)及び\( \ \phi \ \)を用いて表す式を導出せよ。なお，\( \ E \ \)，\( \ V \ \)及び\( \ I \ \)は図に記載の各フェーザの大きさを示す。

(2)　発電機の\( \ V \ \)及び\( \ I \ \)を一定として，力率\( \ \cos \phi \ \)\(\left( 遅れ， \ 0°＜\phi ≦90° \ \right) \)を小さくした場合，\( \ \varepsilon \ \)が大きくなる理由を説明せよ。

(3)　短絡比\( \ K_{\mathrm{SCR}} \ \)を無負荷飽和曲線及び三相短絡特性曲線を用いて導出する方法を説明せよ。

(4)　\( \ K_{\mathrm{SCR}} \ \)と同期リアクタンス\( \ X_{\mathrm{S}} \ \mathrm{[p.u.]} \ \)との関係を示せ。
　また，\( \ V \ \)，\( \ I \ \)及び力率が同じ運転状態のとき，\( \ K_{\mathrm{SCR}} \ \)の小さな発電機の方の\( \ \varepsilon \ \)が大きくなる理由を説明せよ。

(5)　\( \ K_{\mathrm{SCR}}=0.6 \ \)の三相円筒形同期発電機において，三相平衡負荷を発電機に接続し，\( \ V=1 \ \mathrm{p.u.} \ \)一定になるように界磁電流を調整したところ，発電機の\( \ \delta \ \)は\( \ 30° \ \)で力率\( \ \cos \phi \ \)は\( \ 0.9 \ \)(遅れ)であった。この運転状態における\( \ E \ \mathrm{[p.u.]} \ \)，\( \ I \ \mathrm{[p.u.]} \ \)及び出力\( \ P \ \mathrm{[p.u.]} \ \)を求めよ。また，このときの\( \ \varepsilon \ [％] \ \)を求めよ。

【ワンポイント解説】

比較的理解しやすく，過去問でも出題されているような問題です。ただし，スピーディかつ正確に解かないとタイムオーバーとなってしまいます。本設問にて与えられている電圧変動率や短絡比の定義，出力の公式はよく理解しておきましょう。

1.電圧変動率\( \ \varepsilon \ \)の定義
無負荷誘導起電力(相電圧)を\( \ E \ \)，端子電圧(相電圧)を\( \ V \ \)とすると，電圧変動率\( \ \varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {E-V}{V}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] と定義されます。

2.単位法における同期発電機の出力\( \ P \ \)
無負荷誘導起電力(相電圧)を\( \ E \ \)，端子電圧(相電圧)を\( \ V \ \)，電機子電流\( \ I \ \)，同期リアクタンスを\( \ X_{\mathrm {S}} \ \)，内部相差角を\( \ \delta \ \)，力率角を\( \ \phi \ \)とすると，出力\( \ P \ \)は，
\[
\begin{eqnarray}
P&=&VI\cos\phi \\[ 5pt ] &=&\frac {EV}{X_{\mathrm {S}}}\sin {\delta } \\[ 5pt ] \end{eqnarray}
\] となります。

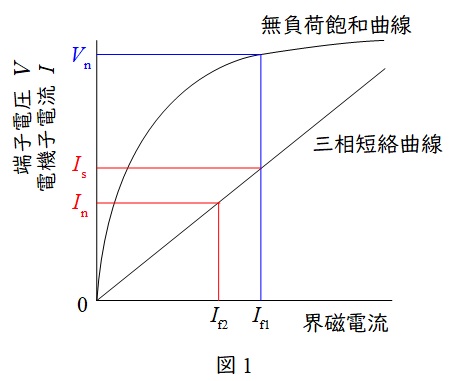
3.同期発電機の特性曲線と短絡比
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm{n}} \ \)は定格電圧，\( \ I_{\mathrm{n}} \ \)は定格電流，\( \ I_{\mathrm{f1}} \ \)は定格電圧を誘起するのに必要な界磁電流，\( \ I_{\mathrm{f1}} \ \)における三相短絡電流を\( \ I_{\mathrm{s}} \ \)，\( \ I_{\mathrm{n}} \ \)に等しい短絡電流を流すのに必要な界磁電流を\( \ I_{\mathrm{f2}} \ \)とすると，短絡比\( \ K_{\mathrm{SCR}} \ \)は，
\[
\begin{eqnarray}
K_{\mathrm{SCR}}&=&\frac {I_{\mathrm{f1}}}{I_{\mathrm{f2}}} \\[ 5pt ] &=&\frac {I_{\mathrm{s}}}{I_{\mathrm{n}}} \\[ 5pt ] \end{eqnarray}
\] と定義されます。

【解答】

(1)\( \ \varepsilon \ \)を\( \ V \ \)，\( \ I \ \)，\( \ X_{\mathrm {S}} \ \)及び\( \ \phi \ \)を用いて表す式
図2の青三角形について三平方の定理を適用すると，
\[
E^{2}=\left( V+X_{\mathrm{S}}I\sin {\phi }\right) ^{2}+\left( X_{\mathrm{S}}I\cos{\phi }\right) ^{2}
\] となるから，\( \ \sin ^{2}\phi +\cos ^{2}\phi = 1 \ \)に注意して整理すると，
\[
\begin{eqnarray}
E^{2} &=& V^{2}+2VX_{\mathrm{S}}I\sin {\phi } +\left( X_{\mathrm{S}}I\right) ^{2} \sin ^{2}{\phi }+\left( X_{\mathrm{S}}I\right) ^{2}\cos ^{2} {\phi } \\[ 5pt ] E^{2} &=& V^{2}+2VX_{\mathrm{S}}I\sin {\phi } +\left( X_{\mathrm{S}}I\right) ^{2} \\[ 5pt ] E &=& \sqrt {V^{2}+2VX_{\mathrm{S}}I\sin {\phi } +\left( X_{\mathrm{S}}I \right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] 電圧変動率の定義に上式を代入すると，
\[
\begin{eqnarray}
\varepsilon &=& \frac {E-V}{V}\times 100 \ [％] \\[ 5pt ] &=& \frac {\sqrt {V^{2}+2VX_{\mathrm{S}}I\sin {\phi } +\left( X_{\mathrm{S}}I\right) ^{2}}-V}{V}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)発電機の\( \ V \ \)及び\( \ I \ \)を一定として，力率\( \ \cos \phi \ \)\(\left( 遅れ， \ 0°＜\phi ≦90° \ \right) \)を小さくした場合，\( \ \varepsilon \ \)が大きくなる理由
\(\left( 遅れ， \ 0°＜\phi ≦90° \ \right) \)において，力率\( \ \cos {\phi } \ \)が小さくなると\( \ \phi \ \)は大きくなり，\( \ \phi \ \)が大きくなると\( \ \sin {\phi } \ \)は大きくなる。題意より，(1)の解答式において，\( \ V \ \)及び\( \ I \ \)は一定となるので，\( \ \sin {\phi } \ \)が大きくなると，電圧変動率\( \ \varepsilon \ \)も大きくなる。

(3)短絡比\( \ K_{\mathrm{SCR}} \ \)を無負荷飽和曲線及び三相短絡特性曲線を用いて導出する方法
ワンポイント解説「3.同期発電機の特性曲線と短絡比」の通り，\( \ V_{\mathrm{n}} \ \)を定格電圧，\( \ I_{\mathrm{n}} \ \)を定格電流，\( \ I_{\mathrm{f1}} \ \)を定格電圧\( \ V_{\mathrm{n}} \ \)を誘起するのに必要な界磁電流，\( \ I_{\mathrm{f1}} \ \)における三相短絡電流を\( \ I_{\mathrm{s}} \ \)，\( \ I_{\mathrm{n}} \ \)に等しい短絡電流を流すのに必要な界磁電流を\( \ I_{\mathrm{f2}} \ \)とすると，短絡比\( \ K_{\mathrm{SCR}} \ \)は，
\[
\begin{eqnarray}
K_{\mathrm{SCR}}&=&\frac {I_{\mathrm{f1}}}{I_{\mathrm{f2}}} \\[ 5pt ] &=&\frac {I_{\mathrm{s}}}{I_{\mathrm{n}}} \\[ 5pt ] \end{eqnarray}
\] と導出することができる。

(4)\( \ K_{\mathrm{SCR}} \ \)と同期リアクタンス\( \ X_{\mathrm{S}} \ \mathrm{[p.u.]} \ \)との関係，また，\( \ V \ \)，\( \ I \ \)及び力率が同じ運転状態のとき，\( \ K_{\mathrm{SCR}} \ \)の小さな発電機の方の\( \ \varepsilon \ \)が大きくなる理由
短絡電流\( \ I_{\mathrm{s}} \ \)は\( \ X_{\mathrm{S}} \ \)，\( \ I_{\mathrm{n}} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm{s}}&=&\frac {I_{\mathrm{n}}}{X_{\mathrm{S}}} \\[ 5pt ] \end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
K_{\mathrm{SCR}}&=&\frac {I_{\mathrm{s}}}{I_{\mathrm{n}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {I_{\mathrm{n}}}{X_{\mathrm{S}}}}{I_{\mathrm{n}}} \\[ 5pt ] &=&\frac {1}{X_{\mathrm{S}}} \\[ 5pt ] \end{eqnarray}
\] となる。(1)より，
\[
\begin{eqnarray}
\varepsilon &=& \frac {\sqrt {V^{2}+2VX_{\mathrm{S}}I\sin {\phi } +\left( X_{\mathrm{S}}I\right) ^{2}}-V}{V}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ X_{\mathrm{S}} \ \)が大きくなる方が電圧変動率\( \ \varepsilon \ \)が大きくなり，\( \ K_{\mathrm{SCR}} \ \)が小さくなる方が電圧変動率\( \ \varepsilon \ \)は大きくなる。

(5)\( \ E \ \mathrm{[p.u.]} \ \)，\( \ I \ \mathrm{[p.u.]} \ \)，出力\( \ P \ \mathrm{[p.u.]} \ \)，\( \ \varepsilon \ [％] \ \)
図2の青三角形において，
\[
\begin{eqnarray}
E\cos \delta &=& V+X_{\mathrm{S}}I\sin \phi　&⇔&　E=\frac {V+X_{\mathrm{S}}I\sin \phi }{\cos \delta } \\[ 5pt ] E\sin \delta &=& X_{\mathrm{S}}I\cos \phi 　&⇔&　E=\frac {X_{\mathrm{S}}I\cos \phi }{\sin \delta }
\end{eqnarray}
\] となるから，\( \ E \ \)を消去し\( \ I \ \)について整理すると，
\[
\begin{eqnarray}
\frac {V+X_{\mathrm{S}}I\sin \phi }{\cos \delta } &=& \frac {X_{\mathrm{S}}I\cos \phi }{\sin \delta } \\[ 5pt ] V+X_{\mathrm{S}}I\sin \phi &=& \frac {X_{\mathrm{S}}I\cos \phi }{\tan \delta } \\[ 5pt ] \frac {X_{\mathrm{S}}I\cos \phi }{\tan \delta }-X_{\mathrm{S}}I\sin \phi &=& V \\[ 5pt ] I &=& \frac {V}{\displaystyle \frac {X_{\mathrm{S}}\cos \phi }{\tan \delta }-X_{\mathrm{S}}\sin \phi } \\[ 5pt ] \end{eqnarray}
\] となるから，\( \ V=1 \ \mathrm{[p.u.]} \ \)，\( \ \displaystyle X_{\mathrm{S}}=\frac {1}{K_{\mathrm{SCR}}}=\frac {1}{0.6}≒1.6667 \ \)，\( \ \cos \phi =0.9 \ \)，\( \ \displaystyle \sin \phi =\sqrt{1-0.9^{2}}≒0.43589 \ \)，\( \ \displaystyle \tan \delta = \tan 30° =\frac {1}{\sqrt {3}} \ \)を代入すると，
\[
\begin{eqnarray}
I &=& \frac {1}{1.6667\times 0.9 \times \sqrt {3}-1.6667\times 0.43589 } \\[ 5pt ] &≒& 0.53430　→ 0.534 \ \mathrm{[p.u.]} \\[ 5pt ] \end{eqnarray}
\] 次に，\( \ \displaystyle E=\frac {X_{\mathrm {S}}I\cos \phi }{\sin \delta } \ \)であり，\( \ \displaystyle \sin \delta = \sin 30° =\frac {1}{2} \ \)であるから，
\[
\begin{eqnarray}
E &=& \frac {X_{\mathrm{S}}I\cos \phi }{\sin \delta } \\[ 5pt ] &=& 1.6667\times 0.53430\times 0.9\times 2 \\[ 5pt ] &≒& 1.6029　→ 1.60 \ \mathrm{[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。出力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=& \frac {EV}{X_{\mathrm{S}}}\sin {\delta } \\[ 5pt ] &=& \frac {1.6029\times 1}{1.6667}\times \frac {1}{2} \\[ 5pt ] &≒& 0.48086　→　0.481 \ \mathrm{[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となり，電圧変動率\( \ \varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=& \frac {E-V}{V}\times 100 \\[ 5pt ] &=& \frac {1.6029-1}{1}\times 100 \\[ 5pt ] &=& 60.29　→　60.3 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。