《機械・制御》〈回転機〉[H28:問1]三相誘導電動機のL形等価回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格線間電圧\( \ \mathrm {200 \ V} \ \)，定格周波数\( \ \mathrm {50 \ Hz} \ \)，\( \ 4 \ \)極の星形結線の三相かご形誘導電動機があり，\( \ \mathrm {L} \ \)形等価回路において\( \ 1 \ \)相一次換算の抵抗値及びリアクタンス値は次の通りである。
　　一次抵抗\( \ r_{1}=0.707 \ \Omega \ \)，リアクタンス\( \ x_{1}+x^{\prime }_{2}=0.439 \ \Omega \ \)
　　二次抵抗\( \ r^{\prime }_{2}=0.710 \ \Omega \ \)，
この電動機が回転速度\( \ \mathrm {1470 \ {min}^{-1}} \ \)で運転しているとき，次の値を求めよ。ただし，鉄損，機械損，励磁電流は無視する。

(1)　一次電流
(2)　二次入力
(3)　電動機の軸出力
(4)　二次銅損
(5)　電動機の効率

【ワンポイント解説】

\( \ \mathrm {L} \ \)形等価回路は二次試験では頻出の内容です。必ずスラスラと描けるようにしておきましょう。\( \ \mathrm {L} \ \)形等価回路が描ければ本問は比較的易しい問題となると思います。

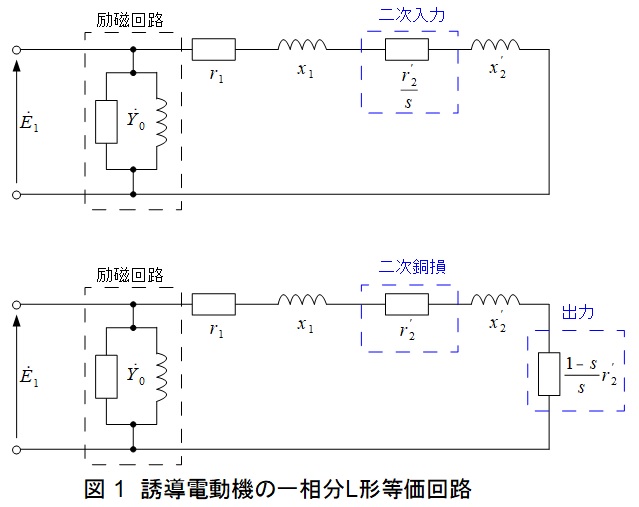
1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
図1が\( \ \mathrm {L} \ \)形等価回路となります。図1の上下の図はいずれも\( \ \mathrm {L} \ \)形等価回路ですが，下図は入力分\( \ \displaystyle \frac {r^{\prime }_{2}}{s} \ \)を銅損分と出力分に分けたものです。

【解答】

(1)一次電流
題意より，この電動機の同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 50}{4} \\[ 5pt ] &=& 1500 \ \mathrm { [ {min}^{-1} ] }
\end{eqnarray}
\] であるから，電動機の滑り\( \ s \ \)は電動機の回転速度\( \ N=\mathrm {1470 \ {min}^{-1}} \ \)であるので，
\[
\begin{eqnarray}
s&=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] &=&\frac {1500-1470}{1500} \\[ 5pt ] &=& 0.02 \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ \mathrm {L} \ \)形等価回路において一次電流\( \ I_{1} \ \)は，励磁電流は無視できることと，相電圧\( \ E_{1} \ \)が\( \ \displaystyle \frac {200}{\sqrt {3}} \ \)であることに注意すると，
\[
\begin{eqnarray}
I_{1}&=&\cfrac {E_{1}}{\sqrt {\left( r_{1}+\cfrac {r_{2}^{\prime }}{s}\right)^{2} +\left( x_{1}+x_{2}^{\prime }\right) ^{2}} } \\[ 5pt ] &=&\cfrac {\cfrac {200}{\sqrt {3}}}{\sqrt {\left( 0.707+\cfrac {0.710}{0.02}\right)^{2} +\left( 0.439\right) ^{2}} } \\[ 5pt ] &≒& 3.1889 \ [ \mathrm {A} ]　→　3.19 \ [ \mathrm {A} ] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)二次入力
\( \ \mathrm {L} \ \)形等価回路において，励磁電流は無視できるので，二次電流\( \ I_{2}^{\prime } \ \)は一次電流\( \ I_{1} \ \)と等しくなる。よって，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\cdot \frac {r_{2}^{\prime }}{s} \cdot {I_{2}^{\prime }}^{2} \\[ 5pt ] &=&3\times \frac {0.710}{0.02} \times {3.1889}^{2} \\[ 5pt ] &≒& 1083.0 \ [ \mathrm {W} ]　→　1.08 \ [ \mathrm {kW} ] \end{eqnarray}
\] と求められる。

(3)電動機の軸出力
(4)二次銅損
電動機の入力\( \ P_{2} \ \)，出力\( \ P_{\mathrm {M}} \ \)，二次銅損\( \ P_{\mathrm {c}} \ \)の関係は，\( \ P_{2}:P_{\mathrm {M}}:P_{\mathrm {c}}=1:\left( 1-s\right) :s \ \)であるから，
\[
\begin{eqnarray}
P_{\mathrm {M}}&=&P_{2}\left( 1-s\right) \\[ 5pt ] &=&1083.0\times \left( 1-0.02\right) \\[ 5pt ] &≒& 1061.3 \ [ \mathrm {W} ]　→　1.06 \ [ \mathrm {kW} ] \end{eqnarray}
\] \[
\begin{eqnarray}
P_{\mathrm {c}}&=&P_{2}\cdot s \\[ 5pt ] &=&1083.0\times 0.02 \\[ 5pt ] &=& 21.66 \ [ \mathrm {W} ]　→　21.7 \ [ \mathrm {W} ] \end{eqnarray}
\] と求められる。

(5)電動機の効率
電動機の一次入力\( \ P_{1} \ \)は，
\[
\begin{eqnarray}
P_{1}&=&3\cdot \left( r_{1} +\frac {r_{2}^{\prime }}{s}\right) \cdot {I_{1}}^{2} \\[ 5pt ] &=&3\times \left( 0.707 +\frac {0.710}{0.02}\right) \times {3.1889}^{2} \\[ 5pt ] &≒& 1104.6 \ [ \mathrm {W} ]　
\end{eqnarray}
\] となるから，電動機の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{M}}{P_{1}}\times 100 \\[ 5pt ] &=&\frac {1061.3}{1104.6}\times 100 \\[ 5pt ] &≒& 96.1 \ [ ％ ]　
\end{eqnarray}
\] と求められる。