《機械・制御》〈回転機〉[R02:問1]三相かご形誘導電動機の回転速度及び周波数の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

三相かご形誘導電動機に関して，次の問に答えよ。

\( \ 4 \ \)極の三相かご形誘導電動機が\( \ 60 \ \mathrm {Hz} \ \)の電源において\( \ 5 \ \mathrm {％} \ \)の滑りで運転している。下記の数値を求めよ。なお，相対速度は単位\( \ \mathrm {[{min}^{-1}]} \ \)を使って答えよ。

(1)　固定子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {0}} \ \)

(2)　回転子と固定子との相対速度の大きさ\( \ N_{\mathrm {m}} \ \)

(3)　固定子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {s}} \ \)

(4)　回転子巻線を流れる電流の周波数\( \ f_{\mathrm {2}} \ \)

(5)　回転子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {r}} \ \)

(6)　回転子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {R}} \ \)

(7)　回転子巻線電流による回転磁界と固定子巻線電流による回転磁界との相対速度の大きさ\( \ N_{\mathrm {sr}} \ \)

【ワンポイント解説】

誘導電動機の回転磁界や回転子の回転速度に関する問題です。
よく出題される等価回路を描き，出力やトルクを求めるといった問題ではなく，誘導電動機のメカニズムを理解しているか問う問題となっています。基本として誘導電動機の回転原理を理解しておくようにしましょう。
(1)の意味がわからないと躓いてしまう問題です。

1.三相誘導電動機の回転原理
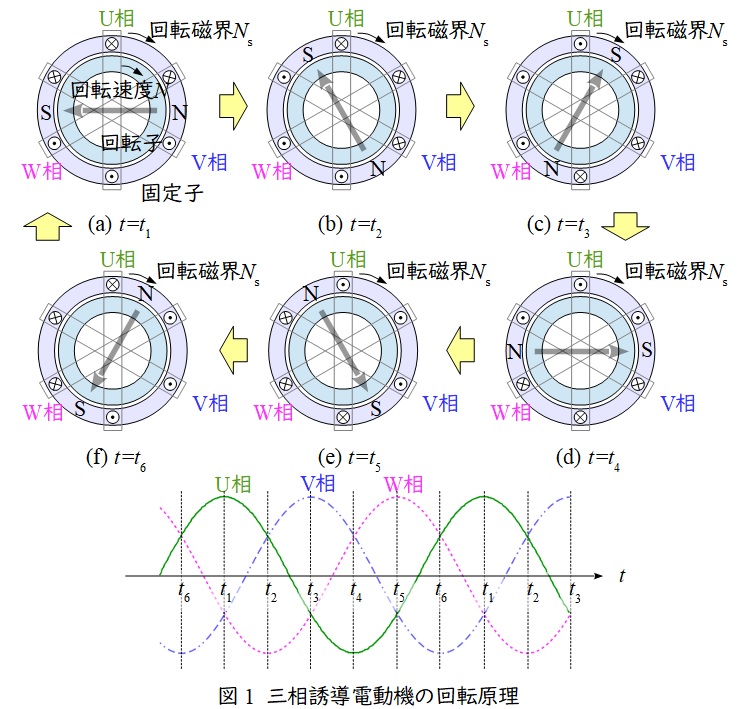
図1に示すように，\( \ 120° \ \)ずつずらして三つの巻線を配置して，三相交流を流します。
時刻\( \ t_{\mathrm {1}} \ \)においては，\( \ \mathrm {U} \ \)相のみ正，\( \ \mathrm {V} \ \)相と\( \ \mathrm {W} \ \)相が負なので，各巻線の電流の向きは(a)のようになり，これにより発生する磁界は右ねじの法則から図の右側から左側に向かって発生します。
その後\( \ t_{\mathrm {1}} \ → \ t_{\mathrm {2}} \ →\cdots → \ t_{\mathrm {6}} \ \)と徐々に変化していくと，合成磁界も回転していくことがわかります。これにより，回転磁界が生まれ，回転磁界により回転子がそれについていく形で移動することになります。このときの回転磁界の回転速度を同期速度といいます。

2.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)固定子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {0}} \ \)
固定子巻線電流による回転磁界と固定子との相対速度の大きさは，固定子は回転しないため，回転磁界の回転速度すなわち同期速度を求めればよい。したがって，ワンポイント解説「2.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」より，
\[
\begin{eqnarray}
N_{\mathrm {0}} &=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 60}{4} \\[ 5pt ] &=&1800 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)回転子と固定子との相対速度の大きさ\( \ N_{\mathrm {m}} \ \)
ワンポイント解説「3.誘導機の滑り\( \ s \ \)」より，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {0}}-N_{\mathrm {m}}}{N_{\mathrm {0}}} \\[ 5pt ] sN_{\mathrm {0}}&=&N_{\mathrm {0}}-N_{\mathrm {m}} \\[ 5pt ] N_{\mathrm {m}}&=&\left( 1-s \right) N_{\mathrm {0}} \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入すると，
\[
\begin{eqnarray}
N_{\mathrm {m}} &=&\left( 1-0.05 \right) \times 1800 \\[ 5pt ] &=&1710 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)固定子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {s}} \ \)
固定子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&N_{\mathrm {0}}-N_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入すると，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&1800-1710 \\[ 5pt ] &=&90 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)回転子巻線を流れる電流の周波数\( \ f_{\mathrm {2}} \ \)
回転子巻線を流れる電流の周波数\( \ f_{\mathrm {2}} \ \)は滑り周波数と呼ばれ，\( \ f_{\mathrm {2}}=sf \ \)で与えられる。したがって，
\[
\begin{eqnarray}
f_{\mathrm {2}} &=&sf \\[ 5pt ] &=&0.05\times 60 \\[ 5pt ] &=&3 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)回転子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {r}} \ \)
回転子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {r}} \ \)は滑り周波数\( \ f_{\mathrm {2}} \ \)の回転速度なので，
\[
\begin{eqnarray}
N_{\mathrm {r}} &=&\frac {120f_{\mathrm {2}}}{p} \\[ 5pt ] &=&\frac {120\times 3}{4} \\[ 5pt ] &=&90 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)回転子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {R}} \ \)
回転子と固定子との相対速度の大きさ\( \ N_{\mathrm {m}} \ \)が\( \ N_{\mathrm {m}}=1710 \ \mathrm {[{min}^{-1}]} \ \)，回転子巻線電流による回転磁界と回転子との相対速度の大きさ\( \ N_{\mathrm {r}} \ \)が\( \ N_{\mathrm {r}}=90 \ \mathrm {[{min}^{-1}]} \ \)であるから，回転子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {R}} &=& N_{\mathrm {m}}+N_{\mathrm {r}} \\[ 5pt ] &=&1710+90 \\[ 5pt ] &=&1800 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(7)回転子巻線電流による回転磁界と固定子巻線電流による回転磁界との相対速度の大きさ\( \ N_{\mathrm {sr}} \ \)
固定子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {0}} \ \)が\( \ N_{\mathrm {0}}=1800 \ \mathrm {[{min}^{-1}]} \ \)，回転子巻線電流による回転磁界と固定子との相対速度の大きさ\( \ N_{\mathrm {R}} \ \)が\( \ N_{\mathrm {R}}=1800 \ \mathrm {[{min}^{-1}]} \ \)であるから，回転子巻線電流による回転磁界と固定子巻線電流による回転磁界との相対速度の大きさ\( \ N_{\mathrm {sr}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {sr}} &=& N_{\mathrm {0}}-N_{\mathrm {R}} \\[ 5pt ] &=&1800-1800 \\[ 5pt ] &=&0 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※回転子巻線電流による回転磁界と固定子巻線電流による回転磁界は等しいことは覚えておきましょう。