《機械・制御》〈回転機〉[R04:問2]三相かご形誘導電動機の諸計算に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格線間電圧\( \ 200 \ \mathrm {V} \ \)，定格周波数\( \ 50 \ \mathrm {Hz} \ \)，\( \ 4 \ \)極の三相かご形誘導電動機がある。この電動機の三相星形結線\( \ 1 \ \)相分の\( \ \mathrm {L} \ \)形等価回路の定数を，励磁アドミタンス\( \ {\dot y}_{0}=0.05-\mathrm {j}0.1 \ \mathrm {S} \ \)，一次巻線抵抗\( \ r_{1}=0.1 \ \mathrm {\Omega } \ \)，一次漏れリアクタンス\( \ x_{1}=0.3 \ \mathrm {\Omega } \ \)，二次抵抗の一次換算値\( \ r_{2}^{\prime }=0.15 \ \mathrm {\Omega } \ \)，二次漏れリアクタンスの一次換算値\( \ x_{2}^{\prime }=0.5 \ \mathrm {\Omega } \ \)とする。この誘導電動機を定格電圧，定格周波数の三相交流電源に接続して，運転している。そのときの回転速度が\( \ 1 \ 455 \ \mathrm {min ^{-1}} \ \)である。この電動機について次の値を求めよ。

(1)　電動機の滑り\( \ s \ \mathrm {[％]} \ \)

(2)　励磁電流\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)

(3)　二次電流の一次換算値\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)

(4)　銅損\( \ \mathrm {[W]} \ \)

(5)　電動機の入力電流\( \ I_{1} \ \mathrm {[A]} \ \)

(6)　電動機の入力力率\( \ [％] \ \)

【ワンポイント解説】

誘導電動機の等価回路を用いた計算問題です。
非常によく出題されるパターンの問題で，多くの受験生が選択したと予想されます。
(3)以降の計算にやや時間を要するので，問題慣れしたら制限時間\( \ 30 \ \)分を測定して練習すると良いでしょう。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \)は二次電流の一次換算値，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。

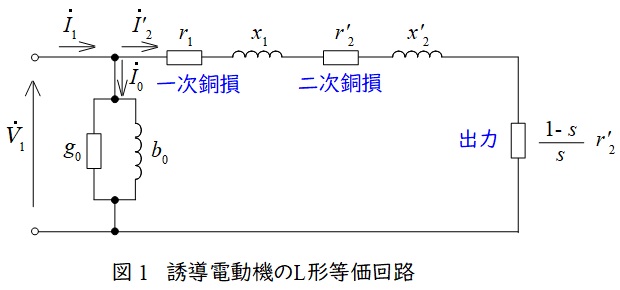
図1より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるから，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ] &=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\] となり，発生するトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ] &=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)電動機の滑り\( \ s \ \mathrm {[％]} \ \)
同期速度\( \ N_{\mathrm {s}} \ \mathrm {[min ^{-1}]} \ \)は，極数が\( \ p=4 \ \)，電源の周波数が\( \ f=50 \ \mathrm {[Hz]} \ \)であるから，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」の通り，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 50}{4} \\[ 5pt ] &=&1 \ 500 \ \mathrm {[min ^{-1}]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，滑り\( \ s \ \mathrm {[％]} \ \)は，定格運転時の回転速度\( \ N=1 \ 455 \ \mathrm {[min ^{-1}]} \ \)であるから，ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}}\times 100 \\[ 5pt ] &=&\frac {1 \ 500-1 \ 455}{1 \ 500}\times 100 \\[ 5pt ] &=&3.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)励磁電流\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)
図1の等価回路において，一次電圧\( \ \displaystyle {\dot V}_{1}=\frac {200}{\sqrt {3}} \ \mathrm {[V]} \ \)，励磁アドミタンス\( \ {\dot y}_{0}=g_{0}+\mathrm {j}b_{0}=0.05-\mathrm {j}0.1 \ \mathrm {[S]} \ \)であるから，
\[
\begin{eqnarray}
{\dot I}_{0} &=&{\dot y}_{0}{\dot V}_{1} \\[ 5pt ] &=&\left( 0.05-\mathrm {j}0.1\right)\times \frac {200}{\sqrt {3}} \\[ 5pt ] &≒&5.7735-\mathrm {j}11.547　→　5.77-\mathrm {j}11.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)二次電流の一次換算値\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)
図1より，
\[
\begin{eqnarray}
{\dot I}_{2}^{\prime } &=&\frac {{\dot V}_{1}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) +\mathrm {j}\left( x_{1}+x_{2}^{\prime }\right) } \\[ 5pt ] &=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{\displaystyle \left( 0.1+\frac {0.15}{0.03}\right) +\mathrm {j}\left( 0.3+0.5\right) } \\[ 5pt ] &≒&\frac {115.47}{5.1 +\mathrm {j}0.8} \\[ 5pt ] &≒&\frac {115.47}{5.1 +\mathrm {j}0.8}\times \frac {5.1 -\mathrm {j}0.8}{5.1 -\mathrm {j}0.8} \\[ 5pt ] &≒&\frac {115.47}{26.65}\times \left( 5.1 -\mathrm {j}0.8\right) \\[ 5pt ] &≒&22.097 -\mathrm {j}3.4663　→　22.1-\mathrm {j}3.47 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)銅損\( \ \mathrm {[W]} \ \)
(3)より，二次電流の大きさ\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\sqrt {22.097^{2}+3.4663^{2}} \\[ 5pt ] &≒&22.367 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，銅損\( \ P_{\mathrm {c}} \ \mathrm {[W]} \ \)は，一次抵抗\( \ r_{1}=0.1 \ \mathrm {[\Omega ]} \ \)と二次抵抗の一次換算\( \ r_{2}^{\prime }=0.15 \ \mathrm {[\Omega ]} \ \)で消費される電力であるから，
\[
\begin{eqnarray}
P_{\mathrm {c}} &=&3r_{1}{I_{2}^{\prime }}^{2}+3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] &=&3{I_{2}^{\prime }}^{2}\left( r_{1}+r_{2}^{\prime }\right) \\[ 5pt ] &=&3\times 22.367^{2}\times \left( 0.1+0.15\right) \\[ 5pt ] &≒&375.21　→　375 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)電動機の入力電流\( \ I_{1} \ \mathrm {[A]} \ \)
(2)及び(3)より，入力電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{1} &=&{\dot I}_{0}+{\dot I}_{2}^{\prime } \\[ 5pt ] &=&\left( 5.7735-\mathrm {j}11.547\right) +\left( 22.097 -\mathrm {j}3.4663\right) \\[ 5pt ] &≒&27.871-\mathrm {j}15.013 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，その大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1} &=&\sqrt {27.871^{2}+15.013^{2}} \\[ 5pt ] &≒&31.657　→　31.7 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)電動機の入力力率\( \ [％] \ \)
入力力率\( \ \cos \theta \ [％] \ \)は，入力電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)の電流の大きさに対する有効電流の大きさであるから，
\[
\begin{eqnarray}
\cos \theta &=&\frac {\mathrm {Re} \left[ {\dot I}_{1}\right] }{I_{1}}\times 100 \\[ 5pt ] &=&\frac {27.871}{31.657}\times 100 \\[ 5pt ] &≒&88.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。