Contents
【問題】
【難易度】★★★☆☆(普通)
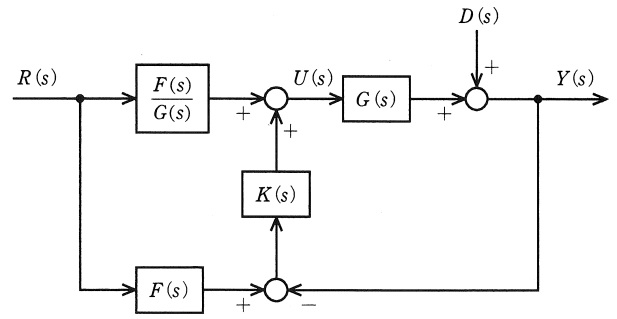
図のフィードバック制御系について,次の問に答えよ。ただし,\( \ R\left( s\right) \ \),\( \ U\left( s\right) \ \),\( \ D\left( s\right) \ \),\( \ Y\left( s\right) \ \)は,それぞれ目標値\( \ r\left( t\right) \ \),操作量\( \ u\left( t\right) \ \),外乱\( \ d\left( t\right) \ \),出力\( \ y\left( t\right) \ \)のラプラス変換を表す。また,\( \ G\left( s\right) \ \)は制御対象の伝達関数,\( \ F\left( s\right) \ \)及び\( \ K\left( s\right) \ \)は補償器の伝達関数を表す。
(1) \( \ R\left( s\right) =0 \ \)のとき,\( \ D\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの伝達関数を求めよ。
(2) \( \ D\left( s\right) =0 \ \)のとき,\( \ R\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの伝達関数を求めよ。
(3) 図において,\( \ \displaystyle G\left( s\right) =\frac {1}{s^{2}} \ \),\( \ \displaystyle F\left( s\right) =\frac {c}{s^{2}+as+b} \ \),\( \ \displaystyle K\left( s\right) =K_{\mathrm {P}}\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s \right) \ \)とおく。\( \ D\left( s\right) =0 \ \)のとき,\( \ R\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの応答特性として,単位ステップ関数の目標値\( \ r\left( t\right) =1 \ \)に対して出力\( \ y\left( t\right) \ \)の定常値が\( \ 1 \ \)となり,かつ,減衰定数が\( \ 0.8 \ \),固有角周波数が\( \ 10 \ \mathrm {[rad / s]} \ \)を満たす\( \ 2 \ \)次系の補償器\( \ F\left( s\right) \ \)の係数\( \ a \ \),\( \ b \ \),\( \ c \ \)を求めよ。
(4) 上記(3)の補償器\( \ K\left( s\right) \ \)の名称を答えよ。また,各係数\( \ K_{\mathrm {P}} \ \),\( \ T_{\mathrm {I}} \ \),\( \ T_{\mathrm {D}} \ \)の名称についても答えよ。
(5) 上記(3)において,\( \ F\left( s\right) \ \)は安定な補償器であり,図の制御系全体の安定性は\( \ F\left( s\right) \ \)にはよらない。制御系全体が安定となるために補償器\( \ K\left( s\right) \ \)の係数\( \ K_{\mathrm {P}} \ \),\( \ T_{\mathrm {I}} \ \),\( \ T_{\mathrm {D}} \ \)が満たさなければならない条件を求めよ。ただし,\( \ K_{\mathrm {P}}\gt 0 \ \),\( \ T_{\mathrm {I}}\gt 0 \ \),\( \ T_{\mathrm {D}}\gt 0 \ \)とする。
【ワンポイント解説】
伝達関数の導出から減衰係数,固有角周波数,安定度まで幅広く取り扱っている問題です。
それぞれの内容の難易度はそれほど高くありませんが,問題量が多く解答にやや時間を要する問題であるため,途中で迷うことなくできるだけ速く解けるようにする練習が必要です。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
u (t) & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
4.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
\( \ 2 \ \)次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
【解答】
(1)\( \ R\left( s\right) =0 \ \)のとき,\( \ D\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの伝達関数
\( \ R\left( s\right) =0 \ \)のとき,制御系の左側から入る信号は全て零となるから,制御系の右側のみを検討すればよい。
\[
\begin{eqnarray}
U\left( s\right) &=&-Y\left( s\right) K\left( s\right) & ・・・・・・・・・・ ①& \\[ 5pt ]
Y\left( s\right) &=&D\left( s\right) +G\left( s\right) U\left( s\right) & ・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
であるから,①を②に代入して整理すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&D\left( s\right) +G\left( s\right) \left\{ -Y\left( s\right) K\left( s\right)\right\} \\[ 5pt ]
&=&D\left( s\right) -K\left( s\right) G\left( s\right) Y\left( s\right) \\[ 5pt ]
Y\left( s\right) +K\left( s\right) G\left( s\right) Y\left( s\right) &=&D\left( s\right) \\[ 5pt ]
\left\{ 1+K\left( s\right) G\left( s\right) \right\} Y\left( s\right) &=&D\left( s\right) \\[ 5pt ]
\frac {Y\left( s\right) }{D\left( s\right) } &=&\frac {1}{1+K\left( s\right) G\left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ D\left( s\right) =0 \ \)のとき,\( \ R\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの伝達関数
\( \ D\left( s\right) =0 \ \)のとき,フィードバック制御系が満たす関係式は,
\[
\begin{eqnarray}
U\left( s\right) &=&R\left( s\right) \cdot \frac {F\left( s\right) }{G\left( s\right) } +\left\{ R\left( s\right) F\left( s\right) -Y\left( s\right) \right\}K\left( s\right) & ・・・・・・ ③& \\[ 5pt ]
Y\left( s\right) &=&G\left( s\right) U\left( s\right) & ・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
であるから,③を④に代入して整理すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&G\left( s\right) \left[ R\left( s\right) \cdot \frac {F\left( s\right) }{G\left( s\right) } +\left\{ R\left( s\right) F\left( s\right) -Y\left( s\right) \right\}K\left( s\right) \right] \\[ 5pt ]
Y\left( s\right) &=& F\left( s\right) R\left( s\right) +\left\{F\left( s\right) R\left( s\right) -Y\left( s\right) \right\}K\left( s\right) G\left( s\right) \\[ 5pt ]
&=& F\left( s\right) R\left( s\right) +K\left( s\right) G\left( s\right) F\left( s\right) R\left( s\right) -K\left( s\right) G\left( s\right) Y\left( s\right) \\[ 5pt ]
Y\left( s\right) +K\left( s\right) G\left( s\right) Y\left( s\right) &=& F\left( s\right) R\left( s\right) +K\left( s\right) G\left( s\right) F\left( s\right) R\left( s\right) \\[ 5pt ]
\left\{ 1 +K\left( s\right) G\left( s\right) \right\} Y\left( s\right) &=& \left\{ 1 +K\left( s\right) G\left( s\right) \right\} F\left( s\right) R\left( s\right) \\[ 5pt ]
Y\left( s\right) &=&F\left( s\right) R\left( s\right) \\[ 5pt ]
\frac {Y\left( s\right) }{R\left( s\right) } &=&F\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)指定された条件を満たす\( \ 2 \ \)次系の補償器\( \ F\left( s\right) \ \)の係数\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)
ワンポイント解説「1.基本的なラプラス変換」の通り,\( \ \displaystyle R\left( s\right) =\frac {1}{s} \ \)であるから,(2)の解答式にこれと\( \ \displaystyle F\left( s\right) =\frac {c}{s^{2}+as+b} \ \)を代入すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&F\left( s\right) R\left( s\right) \\[ 5pt ]
&=&\frac {c}{s^{2}+as+b}\cdot \frac {1}{s} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.最終値の定理」より,出力\( \ y\left( t\right) \ \)の定常値が\( \ 1 \ \)であるから,
\[
\begin{eqnarray}
\displaystyle \lim _{ s \to 0 } sY(s)&=&1 \\[ 5pt ]
\displaystyle \lim _{ s \to 0 } s\left( \frac {c}{s^{2}+as+b}\cdot \frac {1}{s}\right) &=&1 \\[ 5pt ]
\displaystyle \lim _{ s \to 0 } \frac {c}{s^{2}+as+b} &=&1 \\[ 5pt ]
\frac {c}{b} &=&1 \\[ 5pt ]
c &=&b ・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となる。また,ワンポイント解説「4.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の通り,\( \ F\left( s\right) \ \)を\( \ 2 \ \)次遅れの伝達関数の一般式と比較すると,
\[
\begin{eqnarray}
a&=&2\zeta \omega _{\mathrm {n}} \\[ 5pt ]
&=&2\times 0.8 \times 10 \\[ 5pt ]
&=&16 \\[ 5pt ]
b&=&\omega _{\mathrm {n}}^{2} \\[ 5pt ]
&=&10^{2} \\[ 5pt ]
&=&100 \\[ 5pt ]
\end{eqnarray}
\]
と求められ,⑤より\( \ c=b=100 \ \)と求められる。
(4)補償器\( \ K\left( s\right) \ \)及び各係数\( \ K_{\mathrm {P}} \ \),\( \ T_{\mathrm {I}} \ \),\( \ T_{\mathrm {D}} \ \)の名称
\( \ K\left( s\right) \ \):\( \ \mathrm {PID} \ \)補償器
\( \ K_{\mathrm {P}} \ \):比例ゲイン
\( \ T_{\mathrm {I}} \ \):積分時間
\( \ T_{\mathrm {D}} \ \):微分時間
(5)制御系全体が安定となるために補償器\( \ K\left( s\right) \ \)の係数\( \ K_{\mathrm {P}} \ \),\( \ T_{\mathrm {I}} \ \),\( \ T_{\mathrm {D}} \ \)が満たさなければならない条件
制御系全体が安定となるためには(1)で求めた外乱\( \ D\left( s\right) \ \)に対する制御が安定でなければならない。①の解答式に\( \ \displaystyle G\left( s\right) =\frac {1}{s^{2}} \ \),\( \ \displaystyle K\left( s\right) =K_{\mathrm {P}}\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s \right) \ \)を代入すると,
\[
\begin{eqnarray}
\frac {Y\left( s\right) }{D\left( s\right) } &=&\frac {1}{1+K\left( s\right) G\left( s\right) } \\[ 5pt ]
&=&\frac {1}{1+\displaystyle \left\{ K_{\mathrm {P}}\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s \right) \right\} \frac {1}{s^{2}} } \\[ 5pt ]
&=&\frac {s^{3}}{s^{3}+\displaystyle K_{\mathrm {P}}s\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s \right) } \\[ 5pt ]
&=&\frac {s^{3}}{\displaystyle s^{3}+ K_{\mathrm {P}}T_{\mathrm {D}}s^{2}+ K_{\mathrm {P}}s+\frac {K_{\mathrm {P}}}{T_{\mathrm {I}}} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,特性方程式は,
\[
\begin{eqnarray}
s^{3}+ K_{\mathrm {P}}T_{\mathrm {D}}s^{2}+ K_{\mathrm {P}}s+\frac {K_{\mathrm {P}}}{T_{\mathrm {I}}}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.ラウスの安定判別法」により,ラウス表を作成すると,
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & K_{\mathrm {P}} \\
2行 & K_{\mathrm {P}}T_{\mathrm {D}} & \frac {K_{\mathrm {P}}}{T_{\mathrm {I}}} \\
3行 & \frac { K_{\mathrm {P}}^{2}T_{\mathrm {D}}-\frac {K_{\mathrm {P}}}{T_{\mathrm {I}}}}{K_{\mathrm {P}}T_{\mathrm {D}}} & 0 \\
4行 & \frac {K_{\mathrm {P}}}{T_{\mathrm {I}}} & \\
\end{array}
\]
となるので,安定となるためには,
\[
\begin{eqnarray}
\frac { \displaystyle K_{\mathrm {P}}^{2}T_{\mathrm {D}}-\frac {K_{\mathrm {P}}}{T_{\mathrm {I}}}}{K_{\mathrm {P}}T_{\mathrm {D}}}&\gt &0 \\[ 5pt ]
K_{\mathrm {P}}T_{\mathrm {D}}-\frac {1}{T_{\mathrm {I}}}&\gt &0 \\[ 5pt ]
K_{\mathrm {P}}T_{\mathrm {D}}&\gt &\frac {1}{T_{\mathrm {I}}} \\[ 5pt ]
K_{\mathrm {P}}T_{\mathrm {D}}T_{\mathrm {I}}&\gt &1 \\[ 5pt ]
\end{eqnarray}
\]
と満たす必要がある。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは