《機械・制御》〈パワーエレクトロニクス〉[R04:問3]電動機を駆動する電力変換システムに関する計算問題

【問題】

【難易度】★★★★★（難しい）

三相誘導電動機を駆動する電力変換システムに関して，次の問に答えよ。
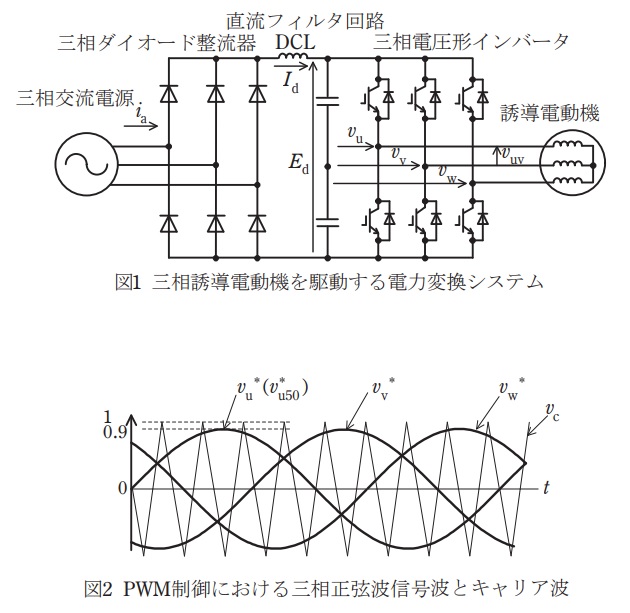
図1は対称三相交流電源，三相ダイオード整流器，直流フィルタ回路，\( \ \mathrm {PWM} \ \)制御三相電圧形インバータ及び三相誘導電動機からなるシステムを示す。ここで，交流電源は電源インピーダンスが無視でき，パワーデバイス及び回路に損失はないものとする。以下の問に答えよ。

(1)　図1において，直流リアクトル\( \ \mathrm {DCL} \ \)に流れる直流電流は一定とすると，直流電圧は三相整流電圧平均値となる。三相交流電源は実効値\( \ 220 \ \mathrm {V} \ \)，\( \ 50 \ \mathrm {Hz} \ \)とすると，直流電圧\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)はいくらであるか，数値で答えよ。

(2)　小問(1)において，誘導電動機を運転したところ，有効電力は\( \ 10 \ \mathrm {kW} \ \)であった。直流電流\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \)はいくらであるか，数値で答えよ。

(3)　三相ダイオード整流器は力率\( \ 1 \ \)で運転している。小問(1)，(2)において，入力の交流電源電流\( \ i_{\mathrm {a}} \ \)の基本波実効値\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)はいくらであるか，数値で答えよ。

次に，図2は，図1のインバータの\( \ \mathrm {PWM} \ \)制御で使われている三相正弦波信号波\( \ v_{\mathrm {u}}^{*} \ \)，\( \ v_{\mathrm {v}}^{*} \ \)，\( \ v_{\mathrm {w}}^{*} \ \)とキャリア波\( \ v_{\mathrm {c}} \ \)を示す。キャリア波の周波数は信号波の周波数に対して十分大きいものとする。以下の問に答えよ。

(4)　信号波(振幅\( \ 0.9 \ \))とキャリア波(振幅\( \ 1 \ \))が図2に示す波形であるときに，直流電圧\( \ E_{\mathrm {d}} \ \)の中点から見たインバータの出力相電圧\( \ v_{\mathrm {u}} \ \)の基本波波高値\( \ V_{\mathrm {up}} \ \)はいくらであるか，数値で答えよ。

(5)　小問(4)において，インバータの\( \ \mathrm {u-v} \ \)相出力線間電圧\( \ v_{\mathrm {uv}} \ \)の基本波実効値\( \ V_{\mathrm {uve}} \ \)はいくらであるか，数値で答えよ。

(6)　インバータは電動機を可変するために\( \ \mathrm {V / f} \ \)一定制御をしている。誘導電動機の定格周波数\( \ 50 \ \mathrm {Hz} \ \)時に定格電圧を発生するための\( \ \mathrm {u} \ \)相信号波が図 2に示す\( \ v_{\mathrm {u}}^{*} \ \)であり，改めてこのときの信号波を\( \ v_{\mathrm {u50}}^{*} \ \)と呼ぶ。出力周波数\( \ 25 \ \mathrm {Hz} \ \)ではどのような\( \ \mathrm {u} \ \)相信号波\( \ v_{\mathrm {u25}}^{*} \ \)とすべきか，信号\( \ v_{\mathrm {u50}}^{*} \ \)を\( \ 4 \ \)周期分書き込んだ図が解答用紙に示してあるので，\( \ v_{\mathrm {u25}}^{*} \ \)を信号の大きさ及び周期が明確に分かるように追記せよ。

【ワンポイント解説】

三相の電力変換システムに関する難問です。
過去問においても難易度差の特に大きいパワーエレクトロニクスですが，本問は三相のシステムであること，設問数が多いこと等を考慮すると\( \ 1 \ \)種でそのまま出題されてもおかしくないような問題でした。
他の問題の難易度を考慮すると，ほとんどの受験生が選択しなかった問題と考えて良いと思います。

1.三相ダイオードブリッジ整流回路の動作
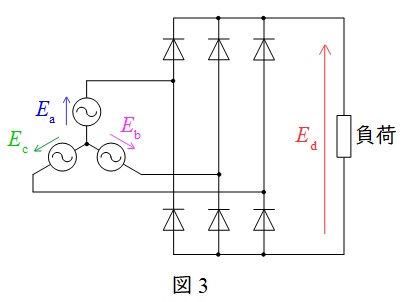
三相ダイオードブリッジ整流回路は三相交流から直流を得る回路で，図3のように\( \ 6 \ \)つのダイオードで構成されています。
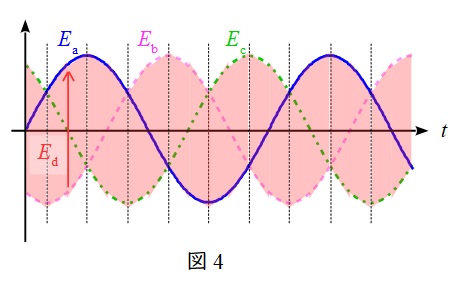
三相交流を流すと，どの時刻においても電流は一番高い電源から一番低い電源に流れるので，出力電圧\( \ E_{\mathrm {d}} \ \)は図4に示すような領域の電圧となり，その平均電圧は基準電圧を\( \ E_{\mathrm {a}}=\sqrt {2}E\sin \omega t \ \)とすると，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left( E_{\mathrm {a}}-E_{\mathrm {b}}\right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \mathrm {d}\omega t \\[ 5pt ] \end{eqnarray}
\] となります。ここで和積の公式\( \ \displaystyle \sin A-\sin B=2\cos \frac {A+B}{2}\sin \frac {A-B}{2} \ \)より，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right)\sin \frac {\pi}{3} \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right) \frac {\sqrt {3}}{2}\mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \sqrt {6}E \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left[ \sin \left( \omega t-\frac {\pi}{3} \right) \right] _{\frac {\pi}{6}}^{\frac {\pi}{2}} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \frac {\pi}{2}-\frac {\pi}{3} \right)- \sin \left( \frac {\pi}{6}-\frac {\pi}{3} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \frac {\pi}{6}- \sin \left( -\frac {\pi}{6} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \frac {1}{2}- \left( -\frac {1}{2} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E \\[ 5pt ] \end{eqnarray}
\] と求められます。

2.三相インバータの動作
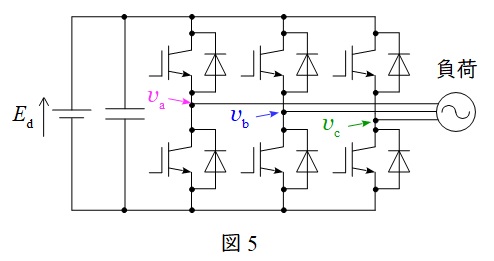
三相インバータは直流から交流を得る回路で，図5のような\( \ 6 \ \)つのスイッチで構成されています。
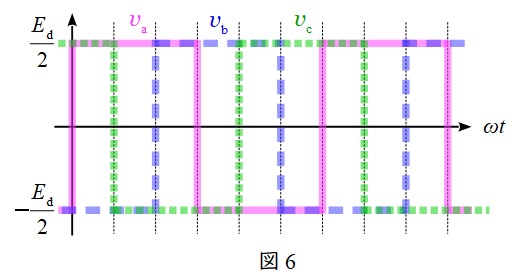
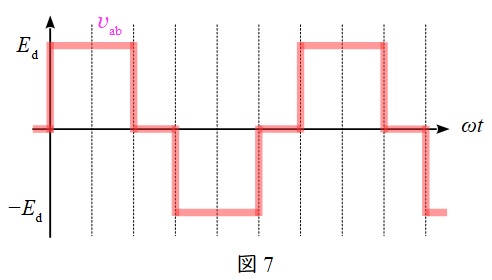
例えば，対応する正負のスイッチを\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずらしてオンオフ制御すると，図6のように\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずれた方形波が得られ，線間電圧を取れば図7のようなより正弦波に近い波形が得られます。
このとき，線間電圧の実効値\( \ V \ \)は，
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }E_{\mathrm {d}}^{2}\mathrm {d}\theta } \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }1\mathrm {d}\theta } \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left[ \theta \right] _{0}^{\frac {2}{3}\pi }} \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left( \frac {2}{3}\pi -0 \right) } \\[ 5pt ] &=&\sqrt {\frac {2}{3}}E_{\mathrm {d}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)直流電圧\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)の値
ワンポイント解説「1.三相ダイオードブリッジ整流回路の動作」の通り，交流電圧の相電圧の実効値が\( \ E \ \mathrm {[V]} \ \)であるとき，直流電圧\( \ \displaystyle E_{\mathrm {d}}=\frac {3\sqrt {6}}{\pi }E \ \)であるから，\( \ \displaystyle E=\frac {220}{\sqrt {3}} \ \mathrm {[V]} \ \)を代入すると，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {3\sqrt {6}}{\pi }E \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }\times \frac {220}{\sqrt {3}} \\[ 5pt ] &≒&297.10　→　297 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)直流電流\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \)の値
題意より，パワーデバイス及び回路に損失はないものとするとなっているので，直流の電力も\( \ P_{\mathrm {d}}=10 \ \mathrm {[kW]} \ \)となる。したがって直流電流\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {d}} &=&\frac {P_{\mathrm {d}}}{E_{\mathrm {d}}} \\[ 5pt ] &=&\frac {10\times 10^{3}}{297.10} \\[ 5pt ] &≒&33.659　→　33.7 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)入力の交流電源電流\( \ i_{\mathrm {a}} \ \)の基本波実効値\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)の値
題意より，パワーデバイス及び回路に損失はないものとするとなっているので，入力電力も\( \ P_{\mathrm {i}}=10 \ \mathrm {[kW]} \ \)となる。三相交流電源の実効値は\( \ V_{\mathrm {i}}=220 \ \mathrm {[V]} \ \)が与えられており，力率が\( \ 1 \ \)であるので，
\[
\begin{eqnarray}
P_{\mathrm {i}} &=&\sqrt {3}V_{\mathrm {i}}I_{\mathrm {a}} \\[ 5pt ] I_{\mathrm {a}}&=&\frac {P_{\mathrm {i}}}{\sqrt {3}V_{\mathrm {i}}} \\[ 5pt ] &=&\frac {10\times 10^{3}}{\sqrt {3}\times 220} \\[ 5pt ] &≒&26.243　→　26.2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)インバータの出力相電圧\( \ v_{\mathrm {u}} \ \)の基本波波高値\( \ V_{\mathrm {up}} \ \)
ワンポイント解説「2.三相インバータの動作」の通り，直流電圧が\( \ \ E_{\mathrm {d}} \ \)であるときの三相インバータの相電圧の基本波波高値は\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)であり，本問においては信号波の振幅が\( \ 0.9 \ \)となっているから，
\[
\begin{eqnarray}
V_{\mathrm {up}} &=&\frac {0.9E_{\mathrm {d}}}{2} \\[ 5pt ] &=&\frac {0.9\times 297.10}{2} \\[ 5pt ] &≒&133.70　→　134 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)出力線間電圧\( \ v_{\mathrm {uv}} \ \)の基本波実効値\( \ V_{\mathrm {uve}} \ \)
(4)より，相電圧の実効値\( \ V_{\mathrm {upe}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {upe}} &=&\frac {V_{\mathrm {up}}}{\sqrt {2}} \\[ 5pt ] &=&\frac {133.70}{\sqrt {2}} \\[ 5pt ] &≒&94.540 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] なので，線間電圧\( \ v_{\mathrm {uv}} \ \)の基本波実効値\( \ V_{\mathrm {uve}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {uve}} &=&\sqrt {3}V_{\mathrm {upe}} \\[ 5pt ] &=&\sqrt {3}\times 94.540 \\[ 5pt ] &≒&163.75　→　164 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

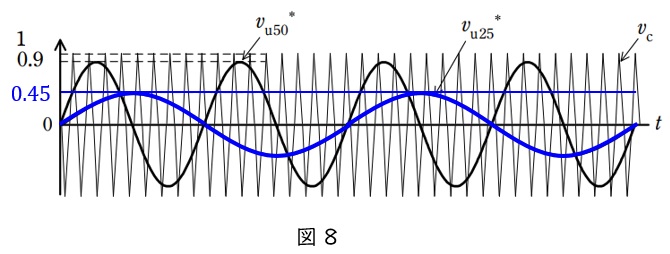
(6)出力周波数\( \ 25 \ \mathrm {Hz} \ \)ではどのような\( \ \mathrm {u} \ \)相信号波\( \ v_{\mathrm {u25}}^{*} \ \)とすべきか
題意より，\( \ \mathrm {V / f} \ \)が一定なので，電圧の波高値は\( \ 0.45 \ \)とし，周波数は\( \ \displaystyle \frac {1}{2} \ \)となるように記載すれば良い。
したがって，図8のようになる。