Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図1のように同一の\( \ 2 \ \)台の単相変圧器\( \ \mathrm {Tr1} \ \)及び\( \ \mathrm {Tr2} \ \)を\( \ \mathrm {V} \ \)結線し,一次側を線間電圧\( \ 400 \ \mathrm {V} \ \)の対称三相交流電源に接続する。一次巻線と二次巻線の巻数は\( \ 4 : 1 \ \)であり,一次及び二次の漏れリアクタンスはそれぞれ\( \ 0.64 \ \mathrm {\Omega } \ \),\( \ 0.21 \ \mathrm {\Omega } \ \)である。三相負荷を二次側に接続すると,一次側線電流には\( \ 30 \ \mathrm {A} \ \)で力率\( \ 1 \ \)の平衡三相電流が流れた。
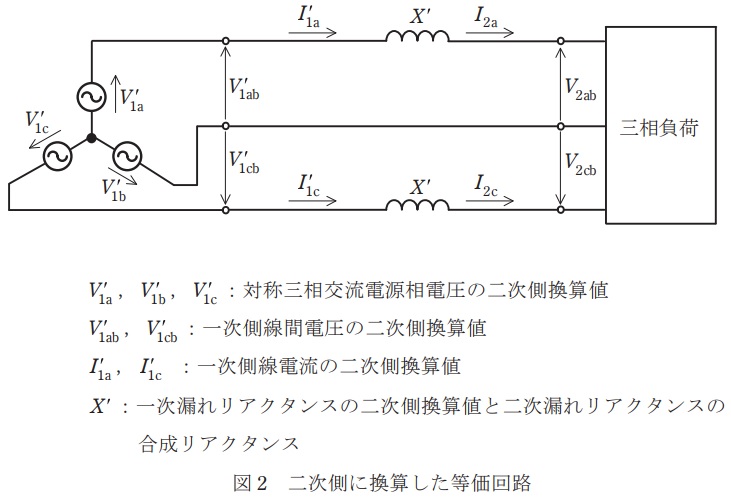
また,図2は,図1を二次側に換算した等価回路である。次の問に答えよ。
ただし,変圧器の励磁電流,鉄損及び巻線抵抗は無視し,変圧器鉄心は磁気飽和しないものとする。
(1) 図2における一次側線間電圧\( \ V_{\mathrm {1ab}} \ \)の二次側換算値\( \ V_{\mathrm {1ab}}^{\prime } \ \)を求めよ。
(2) 図2における一次側線電流\( \ I_{\mathrm {1a}} \ \)の二次側換算値\( \ I_{\mathrm {1a}}^{\prime } \ \)を求めよ。
(3) 図2における一次漏れリアクタンスの二次側換算値と二次漏れリアクタンスの合成リアクタンス\( \ X^{\prime } \ \)を求めよ。
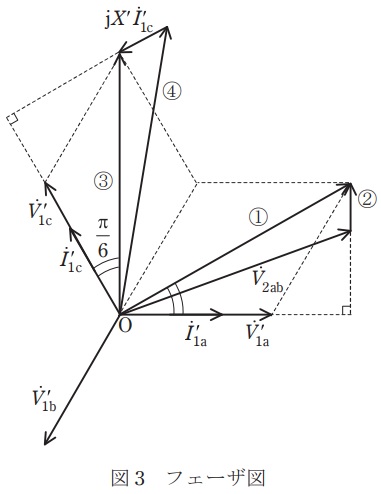
次に,対称三相交流電源における\( \ \mathrm {a} \ \)相の相電圧の二次側換算値を基準として,図2の回路の電圧・電流のフェーザ図を図3に示す。
(4) 図3のフェーザ図中の①,②,③,④に適する電圧のフェーザをそれぞれ答えよ。
(5) 二次側の線間電圧\( \ V_{\mathrm {2ab}} \ \)及び\( \ V_{\mathrm {2cb}} \ \)を求めよ。
(6) \( \ 2 \ \)台の単相変圧器\( \ \mathrm {Tr1} \ \)及び\( \ \mathrm {Tr2} \ \)が負荷に供給する有効電力\( \ P_{\mathrm {1}} \ \)及び\( \ P_{\mathrm {2}} \ \)をそれぞれ求めよ。

【ワンポイント解説】
\( \ \mathrm {V} \ \)結線した変圧器に関する計算問題です。
(1)~(4)が非常に易しい問題であり,平成25年問2に類題も出題されていたので,多くの受験生が選択した問題と予想されます。
(5)及び(6)もそれほど複雑な計算ではないため,慣れてしまえば完答も目指せる問題かと思います。
1.変圧器の巻数比と変圧比,変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \),電圧\( \ V_{1} \ \mathrm {[V]} \ \),電流\( \ I_{1} \ \mathrm {[A]} \ \),二次側の巻数\( \ N_{2} \ \),電圧\( \ V_{2} \ \mathrm {[V]} \ \),電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると,巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は,
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスは電圧を電流で割ったものであるため,一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \),二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ]
&=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ]
&=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ]
&=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ]
&=&a^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図4のような三相対称電源がある時,線間電圧と相電圧の関係は図5のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。

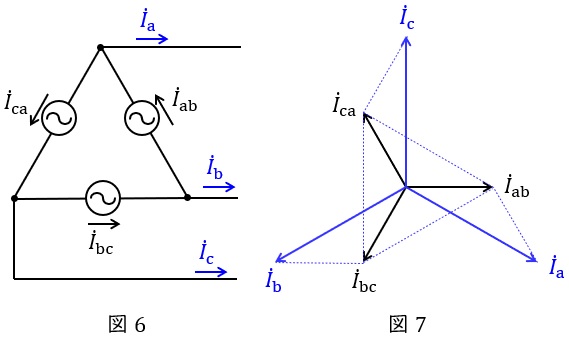
3.\( \ \Delta \ \)結線における相電流と線電流の関係
図6のような三相対称電源がある時,線電流と相電流の関係は図7のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
【解答】
(1)図2における一次側線間電圧\( \ V_{\mathrm {1ab}} \ \)の二次側換算値\( \ V_{\mathrm {1ab}}^{\prime } \ \)
一次巻線と二次巻線の巻数は\( \ 4 : 1 \ \)なので,一次側線間電圧\( \ V_{\mathrm {1ab}}=400 \ \mathrm {[V]} \ \)の二次側換算値\( \ V_{\mathrm {1ab}}^{\prime } \ \mathrm {[V]} \ \)は,ワンポイント解説「1.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
V_{\mathrm {1ab}}^{\prime }&=&\frac {1}{4}V_{\mathrm {1ab}} \\[ 5pt ]
&=&\frac {1}{4}\times 400 \\[ 5pt ]
&=&100 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)図2における一次側線電流\( \ I_{\mathrm {1a}} \ \)の二次側換算値\( \ I_{\mathrm {1a}}^{\prime } \ \)
一次巻線と二次巻線の巻数は\( \ 4 : 1 \ \)なので,一次側線電流\( \ I_{\mathrm {1a}}=30 \ \mathrm {[A]} \ \)の二次側換算値\( \ I_{\mathrm {1a}}^{\prime } \ \mathrm {[A]} \ \)は,ワンポイント解説「1.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
I_{\mathrm {1a}}^{\prime }&=&4I_{\mathrm {1a}} \\[ 5pt ]
&=&4\times 30 \\[ 5pt ]
&=&120 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)図2における一次漏れリアクタンスの二次側換算値と二次漏れリアクタンスの合成リアクタンス\( \ X^{\prime } \ \)
一次漏れリアクタンス\( \ X_{1}=0.64 \ \mathrm {[\Omega ]} \ \)を二次側換算した\( \ X_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
X_{1}^{\prime }&=&\left( \frac {1}{4}\right) ^{2}X_{1} \\[ 5pt ]
&=&\frac {1}{16}\times 0.64 \\[ 5pt ]
&=&0.04 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,合成リアクタンス\( \ X^{\prime } \ \mathrm {[\Omega ]} \ \)は,二次漏れリアクタンス\( \ X_{2}=0.21 \ \mathrm {[\Omega ]} \ \)とおくと,
\[
\begin{eqnarray}
X^{\prime }&=&X_{1}^{\prime }+X_{2} \\[ 5pt ]
&=&0.04+0.21 \\[ 5pt ]
&=&0.25 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)図3のフェーザ図中の①,②,③,④に適する電圧のフェーザ
ワンポイント解説「2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,①は\( \ {\dot V}_{\mathrm {1ab}}^{\prime } \ \),③は\( \ {\dot V}_{\mathrm {1cb}}^{\prime } \ \)である。
図2より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1ab}}^{\prime }&=&{\dot V}_{\mathrm {2ab}}+\mathrm {j}X^{\prime }{\dot I}_{\mathrm {1a}}^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,②は\( \ \mathrm {j}X^{\prime }{\dot I}_{\mathrm {1a}}^{\prime } \ \)となり,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1cb}}^{\prime }&=&{\dot V}_{\mathrm {2cb}}+\mathrm {j}X^{\prime }{\dot I}_{\mathrm {1c}}^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,④は\( \ {\dot V}_{\mathrm {2cb}} \ \)となる。
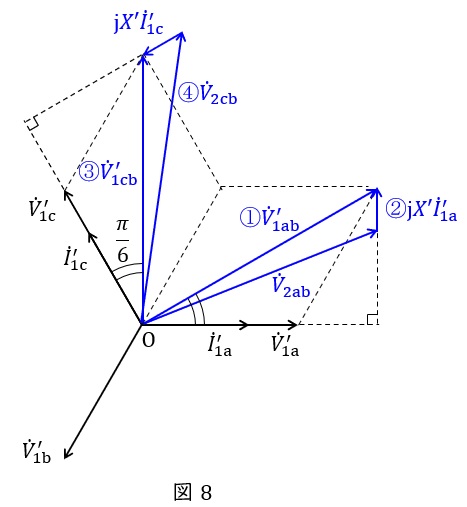
(5)二次側の線間電圧\( \ V_{\mathrm {2ab}} \ \)及び\( \ V_{\mathrm {2cb}} \ \)
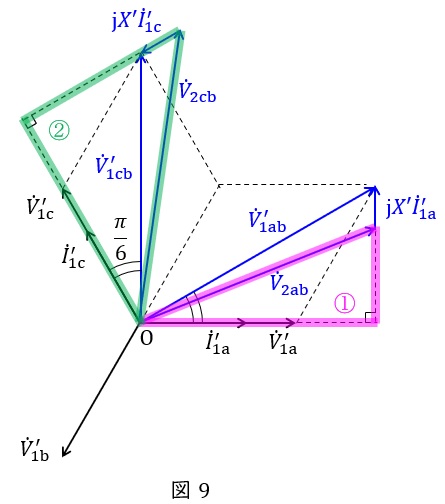
図9の①及び②の三角形に三平方の定理を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {2ab}}&=&\sqrt {\left( V_{\mathrm {1ab}}^{\prime }\cos \frac {\pi}{6} \right) ^{2}+\left( V_{\mathrm {1ab}}^{\prime }\sin \frac {\pi}{6} -X^{\prime }I_{\mathrm {1a}}^{\prime }\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\left( 100 \times \frac {\sqrt {3}}{2} \right) ^{2}+\left( 100 \times \frac {1}{2} -0.25\times 120\right) ^{2}} \\[ 5pt ]
&=&\sqrt {7 \ 500+400} \\[ 5pt ]
&≒&88.882 → 88.9 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {2cb}}&=&\sqrt {\left( V_{\mathrm {1cb}}^{\prime }\cos \frac {\pi}{6} \right) ^{2}+\left( V_{\mathrm {1cb}}^{\prime }\sin \frac {\pi}{6} +X^{\prime }I_{\mathrm {1c}}^{\prime }\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\left( 100 \times \frac {\sqrt {3}}{2} \right) ^{2}+\left( 100 \times \frac {1}{2} +0.25\times 120\right) ^{2}} \\[ 5pt ]
&=&\sqrt {7 \ 500+6 \ 400} \\[ 5pt ]
&≒&117.90 → 118 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)\( \ \mathrm {Tr1} \ \)及び\( \ \mathrm {Tr2} \ \)が負荷に供給する有効電力\( \ P_{\mathrm {1}} \ \)及び\( \ P_{\mathrm {2}} \ \)
題意より,変圧器の損失は無視できるので,一次側入力と二次側の出力は等しい。したがって,\( \ \mathrm {Tr1} \ \)に加わる一次側電圧\( \ V_{\mathrm {1ab}}=400 \ \mathrm {[V]} \ \),一次側電流\( \ I_{\mathrm {1a}}=30 \ \mathrm {[A]} \ \)であり,図8より電圧と電流の位相差が\( \ \displaystyle \frac {\pi }{6} \ \mathrm {[rad]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {1ab}}I_{\mathrm {1a}}\cos \frac {\pi}{6} \\[ 5pt ]
&=&400\times 30\times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&10 \ 392 \ \mathrm {[W]} → 10.4 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,同様に,\( \ \mathrm {Tr2} \ \)に加わる一次側電圧\( \ V_{\mathrm {1cb}}=400 \ \mathrm {[V]} \ \),一次側電流\( \ I_{\mathrm {1c}}=30 \ \mathrm {[A]} \ \)であり,図8より電圧と電流の位相差が\( \ \displaystyle \frac {\pi }{6} \ \mathrm {[rad]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {2}}&=&V_{\mathrm {1cb}}I_{\mathrm {1c}}\cos \frac {\pi}{6} \\[ 5pt ]
&=&400\times 30\times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&10 \ 392 \ \mathrm {[W]} → 10.4 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは