Contents
【問題】
【難易度】★★★★☆(やや難しい)
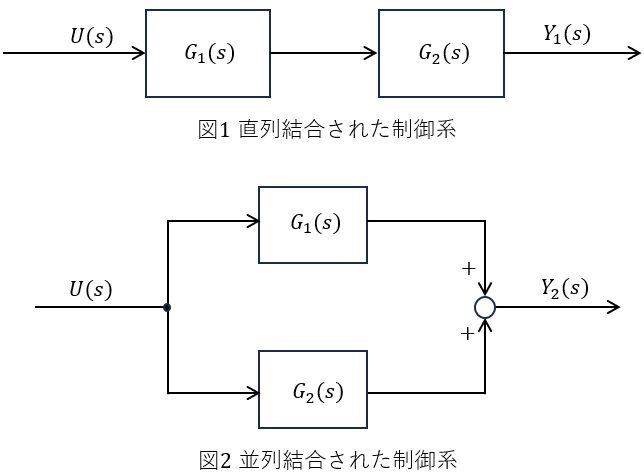
伝達関数\( \ G_{1} (s) \ \),\( \ G_{2} (s) \ \)に対して図1のように直列結合した制御系と図2のように並列結合した制御系が与えられている。\( \ U (s) \ \)は入力量,\( \ Y_{1} (s) \ \)は直列結合した場合の出力量,\( \ Y_{2} (s) \ \)は並列結合した場合の出力量をあらわしている。\( \ U (s) \ \),\( \ Y_{1} (s) \ \),\( \ Y_{2} (s) \ \)は時間信号\( \ u (t) \ \),\( \ y_{1} (t) \ \),\( \ y_{2} (t) \ \)をそれぞれラプラス変換したものである。
伝達関数\( \ G_{1} (s) \ \),\( \ G_{2} (s) \ \)が,
\[
\begin{eqnarray}
G_{1} (s) &=&\frac {3}{s+2}, G_{2} (s) &=&\frac {5}{s^{2}+5s+6} \\[ 5pt ]
\end{eqnarray}
\]
のように与えられているとき,以下の問に答えよ。
(1) 図1の直列結合された制御系の\( \ U (s) \ \)から\( \ Y_{1} (s) \ \)の伝達関数を求めよ。なお,伝達関数は,一つの有理関数で表すとし,分母及び分子は\( \ s \ \)の多項式で示すこと。
(2) (1)で求めた直列結合された伝達関数に単位ステップ信号を加えたときの出力量\( \ Y_{1} (s) \ \)の定常値を求めよ。
(3) 図2の並列結合された制御系のインパルス信号を加えたときの\( \ Y_{2} (s) \ \)の時間応答を求めよ。
(4) (3)で求めた並列結合された伝達関数に\( \ u(t)=2\mathrm {e}^{-t} \ \)を加えたときの\( \ Y_{2} (s) \ \)の時間応答を求めよ。
(5) (3)で求めた並列結合された伝達関数の周波数応答において,周波数を十分に大きくしたときの位相を求めよ。
【ワンポイント解説】
直並列された制御系の伝達関数や時間応答を考える問題です。
解法自体は難解なものは多くありませんが,計算量が多く問題を解くのに時間がかかる問題です。
試験本番でそこまで判断することは厳しいかもしれませんが,逆ラプラス変換が絡んでくると時間がかかる場合が多いことは知っておくとよいかと思います。
もちろん計算力に自信があれば選択しても良い問題です。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
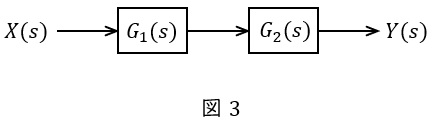
図3のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
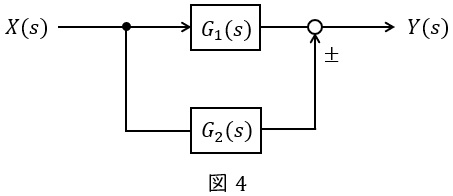
図4のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
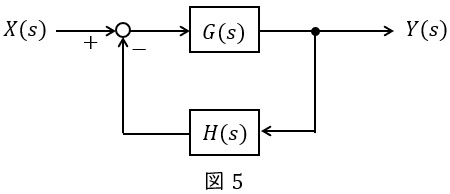
図5のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)図1の\( \ U (s) \ \)から\( \ Y_{1} (s) \ \)の伝達関数
ワンポイント解説「2.ブロック線図の考え方」の通り,図1のブロック線図においては,
\[
\begin{eqnarray}
Y_{1} (s)&=&G_{1} (s)G_{2} (s)U (s) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,伝達関数\( \ \displaystyle W_{1} (s)=\frac {Y_{1} (s)}{U (s)} \ \)は,
\[
\begin{eqnarray}
\frac {Y_{1} (s) }{U (s) }&=&G_{1} (s)G_{2} (s) \\[ 5pt ]
W_{1} (s)&=&\frac {3}{s+2}\cdot \frac {5}{s^{2}+5s+6} \\[ 5pt ]
&=&\frac {15}{s^{3}+7s^{2}+16s+12} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)(1)の伝達関数に単位ステップ信号を加えたときの\( \ Y_{1} (s) \ \)の定常値
(1)解答式より,
\[
\begin{eqnarray}
Y_{1} (s) &=&\frac {15}{s^{3}+7s^{2}+16s+12}U (s) \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.基本的なラプラス変換」の通り,単位ステップ信号のラプラス変換は\( \ \displaystyle \frac {1}{s} \ \)であるので,これを\( \ U (s) \ \)に代入すると,
\[
\begin{eqnarray}
Y_{1} (s) &=&\frac {15}{s^{3}+7s^{2}+16s+12}\cdot \frac {1}{s} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ Y_{1} (s) \ \)の定常値は,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } y_{1}(t)&=&\displaystyle \lim _{ s \to 0 } sY_{1} (s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( s\cdot \frac {15}{s^{3}+7s^{2}+16s+12}\cdot \frac {1}{s}\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( \frac {15}{s^{3}+7s^{2}+16s+12}\right) \\[ 5pt ]
&=&\frac {15}{0+0+0+12} \\[ 5pt ]
&=&1.25 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)図2の制御系にインパルス信号を加えたときの\( \ Y_{2} (s) \ \)の時間応答
ワンポイント解説「2.ブロック線図の考え方」の通り,図2のブロック線図においては,
\[
\begin{eqnarray}
Y_{2} (s)&=&\left\{ G_{1} (s)+G_{2} (s)\right\} U (s) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,伝達関数\( \ \displaystyle W_{2} (s)=\frac {Y_{2} (s)}{U (s)} \ \)は,
\[
\begin{eqnarray}
\frac {Y_{2} (s) }{U (s) }&=&G_{1} (s)+G_{2} (s) \\[ 5pt ]
W_{2} (s)&=&\frac {3}{s+2}+ \frac {5}{s^{2}+5s+6} \\[ 5pt ]
&=&\frac {3}{s+2}+ \frac {5}{\left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac {3\left( s+3\right) }{\left( s+2\right) \left( s+3\right) }+ \frac {5}{\left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac { 3s+9+5}{\left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac { 3s+14}{\left( s+2\right) \left( s+3\right) } ・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。この式を部分分数分解するために,\( \ \displaystyle W_{2} (s)=\frac {A}{s+2}+\frac {B}{s+3} \ \)とおくと,
\[
\begin{eqnarray}
W_{2} (s)&=&\frac {A}{s+2}+\frac {B}{s+3} \\[ 5pt ]
&=&\frac {A\left( s+3\right) +B\left( s+2\right) }{\left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac {\left( A+B\right) s+3A+2B}{\left( s+2\right) \left( s+3\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるから,①式と係数比較すると,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
A+B &=& 3 &・・・・・・・・・・・・ ②& \\[ 5pt ]
3A+2B &=& 14 &・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
となり,\( \ ③-②\times 2 \ \)及び\( \ ②\times 3-③ \ \)より,
\[
\begin{eqnarray}
A&=&8 \\[ 5pt ]
B&=&-5 \\[ 5pt ]
\end{eqnarray}
\]
となる。よって伝達関数は,
\[
\begin{eqnarray}
W_{2} (s)&=&\frac {8}{s+2}-\frac {5}{s+3} \\[ 5pt ]
\end{eqnarray}
\]
となる。続いて,ワンポイント解説「1.基本的なラプラス変換」の通り,単位インパルス信号のラプラス変換は\( \ \displaystyle 1 \ \)であるので,これを\( \ U (s) \ \)に代入すると,
\[
\begin{eqnarray}
\frac {Y_{2} (s)}{U (s)} &=&\frac {8}{s+2}-\frac {5}{s+3} \\[ 5pt ]
Y_{2} (s)&=&\frac {8}{s+2}-\frac {5}{s+3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,逆ラプラス変換すれば,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
y_{2} (t)&=&8\mathrm {e}^{-2t}-5\mathrm {e}^{-3t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)(3)の伝達関数に\( \ u(t)=2\mathrm {e}^{-t} \ \)を加えたときの\( \ Y_{2} (s) \ \)の時間応答
\( \ u(t)=2\mathrm {e}^{-t} \ \)のラプラス変換は\( \ \displaystyle U(s)=\frac {2}{s+1} \ \)であるので\( \ Y_{2} (s) \ \)は,①式を用いて,
\[
\begin{eqnarray}
Y_{2} (s) &=&\frac { 3s+14}{\left( s+2\right) \left( s+3\right) }\cdot \frac {2}{s+1} \\[ 5pt ]
&=&\frac { 6s+28}{\left( s+1\right) \left( s+2\right) \left( s+3\right) } ・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となる。この式を部分分数分解するために,\( \ \displaystyle Y_{2} (s)=\frac {C}{s+1}+\frac {D}{s+2}+\frac {E}{s+3} \ \)とおくと,
\[
\begin{eqnarray}
Y_{2} (s)&=&\frac {C}{s+1}+\frac {D}{s+2}+\frac {E}{s+3} \\[ 5pt ]
&=&\frac {C\left( s+2\right) \left( s+3\right) +D\left( s+1\right) \left( s+3\right) +E\left( s+1\right) \left( s+2\right) }{\left( s+1\right) \left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac {C\left( s^{2}+5s+6\right) +D\left( s^{2}+4s+3\right) +E\left( s^{2}+3s+2\right) }{\left( s+1\right) \left( s+2\right) \left( s+3\right) } \\[ 5pt ]
&=&\frac {\left( C+D+E\right) s^{2} +\left( 5C+4D+3E\right) s+6C+3D+2E}{\left( s+1\right) \left( s+2\right) \left( s+3\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるから,④式と係数比較すると,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
C+D+E &=& 0 &・・・・・・・・ ⑤& \\[ 5pt ]
5C+4D+3E &=& 6 &・・・・・・・・ ⑥& \\[ 5pt ]
6C+3D+2E &=& 28 &・・・・・・・・ ⑦& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
となり,\( \ ⑥-⑤\times 3 \ \)及び\( \ ⑦-⑤\times 2 \ \)より,
\[
\begin{eqnarray}
2C+D&=&6 &・・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
4C+D&=&28 &・・・・・・・・・・・・・・・ ⑨& \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに\( \ ⑨-⑧ \ \)より,
\[
\begin{eqnarray}
2C&=&22 \\[ 5pt ]
C&=&11 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを⑧に代入すれば,
\[
\begin{eqnarray}
2\times 11+D&=&6 \\[ 5pt ]
D&=&-16 \\[ 5pt ]
\end{eqnarray}
\]
となり,⑤式より,
\[
\begin{eqnarray}
E &=& -C-D \\[ 5pt ]
&=&-11+16 \\[ 5pt ]
&=&5 \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,
\[
\begin{eqnarray}
Y_{2} (s)&=&\frac {11}{s+1}-\frac {16}{s+2}+\frac {5}{s+3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを逆ラプラス変換すれば,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
y_{2} (t)&=&11\mathrm {e}^{-t}-16\mathrm {e}^{-2t}+5\mathrm {e}^{-3t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【補足】
ヘビサイトの展開定理という数学の公式を用いると,
\[
\begin{eqnarray}
C&=&\left. \left( s+1\right) \cdot \frac { 6s+28}{\left( s+1\right) \left( s+2\right) \left( s+3\right) }\right| _{s=-1} \\[ 5pt ]
&=&\left. \frac { 6s+28}{\left( s+2\right) \left( s+3\right) }\right| _{s=-1} \\[ 5pt ]
&=&11 \\[ 5pt ]
D&=&\left. \left( s+2\right) \cdot \frac { 6s+28}{\left( s+1\right) \left( s+2\right) \left( s+3\right) }\right| _{s=-2} \\[ 5pt ]
&=&\left. \frac { 6s+28}{\left( s+1\right) \left( s+3\right) }\right| _{s=-2} \\[ 5pt ]
&=&-16 \\[ 5pt ]
E&=&\left. \left( s+3\right) \cdot \frac { 6s+28}{\left( s+1\right) \left( s+2\right) \left( s+3\right) }\right| _{s=-3} \\[ 5pt ]
&=&\left. \frac { 6s+28}{\left( s+1\right) \left( s+2\right) }\right| _{s=-3} \\[ 5pt ]
&=&5 \\[ 5pt ]
\end{eqnarray}
\]
と求められ,部分分数分解より幾分早く計算可能です。詳しく知りたい方は数学のテキスト等を参照して下さい。
(5)(3)の伝達関数の周波数応答において,周波数を十分に大きくしたときの位相
(3)の\( \ W_{2} (s) \ \)の周波数伝達関数\( \ W_{2} (\mathrm {\mathrm {j}\omega }) \ \)は,
\[
\begin{eqnarray}
W_{2} (\mathrm {j}\omega ) &=&\frac {8}{2+\mathrm {j}\omega }-\frac {5}{3+\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
となり,周波数が非常に大きいすなわち\( \ \omega \ \)が非常に大きいとき,
\[
\begin{eqnarray}
W_{2} (\mathrm {j}\omega ) &≃&\frac {8}{\mathrm {j}\omega }-\frac {5}{\mathrm {j}\omega } \\[ 5pt ]
&=&-\mathrm {j}\frac {8}{\omega }+\mathrm {j}\frac {5}{\omega } \left( ∵\frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j} \right)\\[ 5pt ]
&=&-\mathrm {j}\frac {3}{\omega } \\[ 5pt ]
\end{eqnarray}
\]
となるため,位相は\( \ -90° \ \)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは