Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,静電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値(最も近い数値)を解答群の中から選び,その記号をマークシートに記入しなさい。
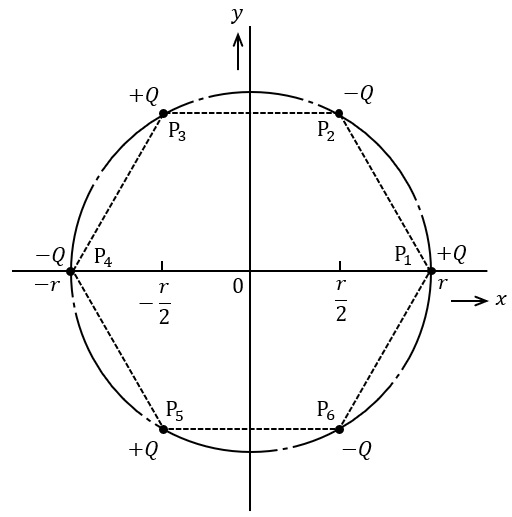
図のように,真空中に\( \ 6 \ \)個の電荷が\( \ 1 \ \)辺\( \ r \ \)の正六角形の頂点\( \ \mathrm {P}_{1} \ \),\( \ \mathrm {P}_{2} \ \),\( \ \mathrm {P}_{3} \ \),\( \ \mathrm {P}_{4} \ \),\( \ \mathrm {P}_{5} \ \),\( \ \mathrm {P}_{6} \ \)に置かれている。各電荷の絶対値は等しく\( \ Q \ \)であるが,\( \ \mathrm {P}_{1} \ \),\( \ \mathrm {P}_{3} \ \),\( \ \mathrm {P}_{5} \ \)にある電荷は正で,\( \ \mathrm {P}_{2} \ \),\( \ \mathrm {P}_{4} \ \),\( \ \mathrm {P}_{6} \ \)にある電荷は負である。この六角形の重心を原点に取れば,各頂点は,中心を原点とする半径\( \ r \ \)の同周上にある。なお,真空の誘電率を\( \ \varepsilon _{0} \ \)とする。
このとき,\( \ \mathrm {P}_{1} \ \)に置かれた電荷に働く力は,他の電荷との間に発生する個々の力を合成すれば求められる。ここでは,次の手順で求めよう。
まず,\( \ \mathrm {P}_{1} \ \)に対し\( \ \mathrm {P}_{4} \ \)の電荷だけに注目すると,働く力の大きさは,\( \displaystyle \ F_{4}=\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \ \fbox { (1) } \ \)である。次に,\( \ \mathrm {P}_{1} \ \)に対し\( \ \mathrm {P}_{2} \ \)と\( \ \mathrm {P}_{6} \ \)に置かれた\( \ 2 \ \)個の電荷だけによる力の大きさは,\( \displaystyle \ F_{26}=\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \ \fbox { (2) } \ \)である。さらに,\( \ \mathrm {P}_{1} \ \)に対し\( \ \mathrm {P}_{3} \ \)と\( \ \mathrm {P}_{5} \ \)に置かれた\( \ 2 \ \)個の電荷だけによる力の大きさは,\( \displaystyle \ F_{35}=\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \ \fbox { (3) } \ \)である。最終的に,それぞれの力の大きさ\( \ F_{4} \ \),\( \ F_{26} \ \),\( \ F_{35} \ \)を,向きを考慮して合成すれば,求める力の大きさは,\( \displaystyle \ F=\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \ \fbox { (4) } \ \)となる。また,原点における合成電界に注目すれば,その大きさは\( \ \fbox { (5) } \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 1.41 &(ロ)& 0.25 &(ハ)& 1.73 \\[ 5pt ]
&(ニ)& 0.14 &(ホ)& 0.33 &(ヘ)& 0 \\[ 5pt ]
&(ト)& 3 &(チ)& 0.58 &(リ)& 0.82 \\[ 5pt ]
&(ヌ)& 1 &(ル)& 0.4 &(ヲ)& 2 \\[ 5pt ]
&(ワ)& 0.2 &(カ)& 0.707 &(ヨ)& 0.67 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
正六角形上に置かれた電荷に働く力とそれらの電荷による電界の大きさを求める問題です。
求められる電磁気の知識はあまり多くなく,数学の幾何的な能力が問われている問題です。解答に示しているようにしっかりと図示して考えることが重要です。
1.クーロンの法則
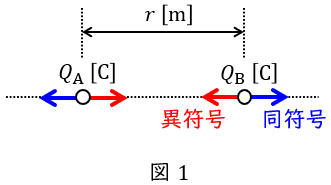
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \),\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。このとき,\( \ Q_{\mathrm {A}} \ \),\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力(反発する力),異符号である場合には引力(引き合う力)が働きます。
2.真空中の電界の大きさ
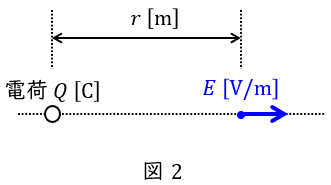
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時,電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電界の大きさ\( \ E \ \mathrm {[N / C]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。この場所に電荷\( \ q \ \mathrm {[C]} \ \)の電荷を置けば,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
の力が働きます。
【解答】
(1)解答:ロ
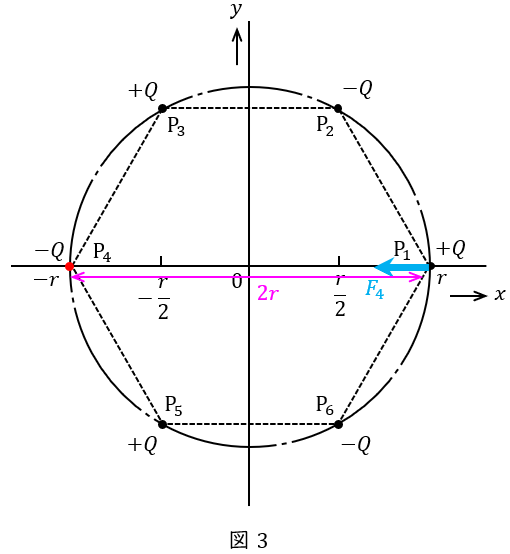
図3に示すように,\( \ \mathrm {P}_{4} \ \)の電荷は\( \ -Q \ \)なので\( \ \mathrm {P}_{1} \ \)の電荷とは引き合い,その距離は\( \ 2r \ \)であるから,働く力の大きさ\( \ F_{4} \ \)は,ワンポイント解説「1.クーロンの法則」の通り,
\[
\begin{eqnarray}
F_{4} &=&\frac {Q\cdot Q}{4\pi \varepsilon _{0}\left( 2r\right) ^{2}} \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \frac {1}{4} \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 0.25 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヌ
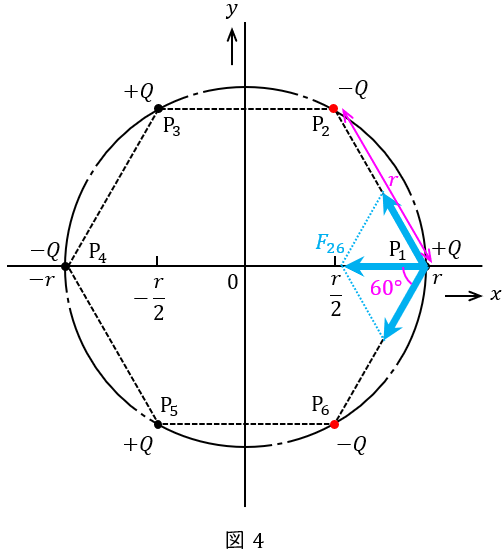
図4に示すように\( \ \mathrm {P}_{2} \ \)と\( \ \mathrm {P}_{6} \ \)の電荷は\( \ -Q \ \)なので\( \ \mathrm {P}_{1} \ \)の電荷とは引き合い,正六角形上の点なので\( \ x \ \)軸とのなす角はともに\( \ 60^{\circ } \ \),その距離はともに\( \ r \ \)である。図4の通り\( \ y \ \)軸成分の力は互いに打ち消し合うので,働く力の大きさ\( \ F_{26} \ \)は,ワンポイント解説「1.クーロンの法則」の通り,
\[
\begin{eqnarray}
F_{26} &=&\frac {Q\cdot Q}{4\pi \varepsilon _{0}r^{2}}\cos 60^{\circ } \times 2 \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \frac {1}{2} \times 2 \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
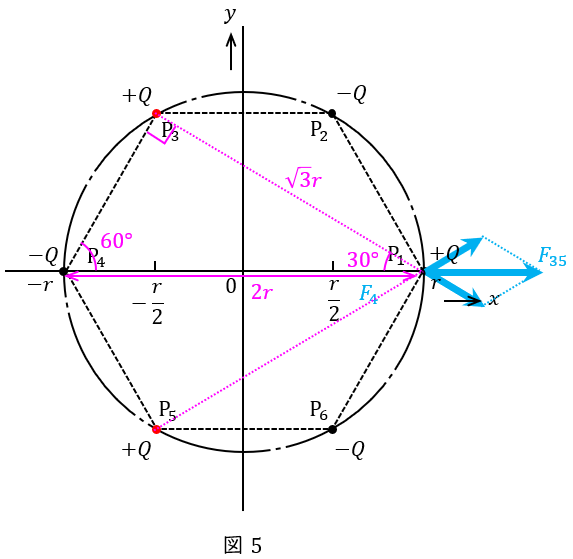
図5に示すように\( \ \mathrm {P}_{3} \ \)と\( \ \mathrm {P}_{5} \ \)の電荷は\( \ +Q \ \)なので\( \ \mathrm {P}_{1} \ \)の電荷とは反発し合い,円周の正六角形上の点なので,直角三角形の関係から\( \ x \ \)軸とのなす角はともに\( \ 30^{\circ } \ \),その距離はともに\( \ \sqrt {3}r \ \)である。図5の通り\( \ y \ \)軸成分の力は互いに打ち消し合うので,働く力の大きさ\( \ F_{35} \ \)は,ワンポイント解説「1.クーロンの法則」の通り,
\[
\begin{eqnarray}
F_{35} &=&\frac {Q\cdot Q}{4\pi \varepsilon _{0}\left( \sqrt {3}r\right) ^{2}}\cos 30^{\circ } \times 2 \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \frac {1}{3} \times \frac {\sqrt {3}}{2}\times 2 \\[ 5pt ]
&≒&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 0.58 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
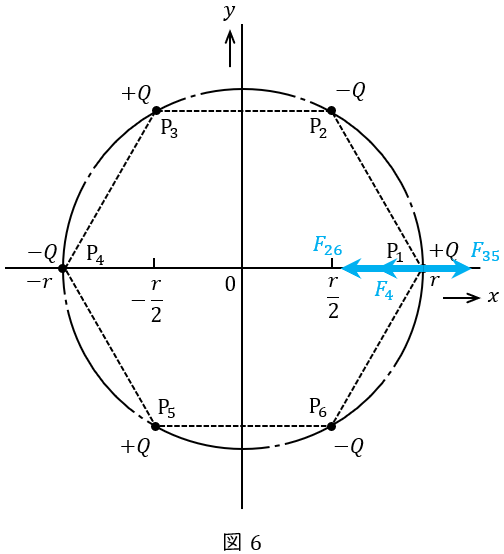
(1)~(3)より,\( \ F_{4} \ \),\( \ F_{26} \ \),\( \ F_{35} \ \)を合成すれば図6のようになり,その大きさ\( \ F \ \)は,
\[
\begin{eqnarray}
F &=&F_{4}+F_{26}-F_{35} \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 0.25+\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 1-\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 0.58 \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times \left( 0.25+ 1- 0.58 \right) \\[ 5pt ]
&=&\frac {Q^{2}}{4\pi \varepsilon _{0}r^{2}}\times 0.67 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
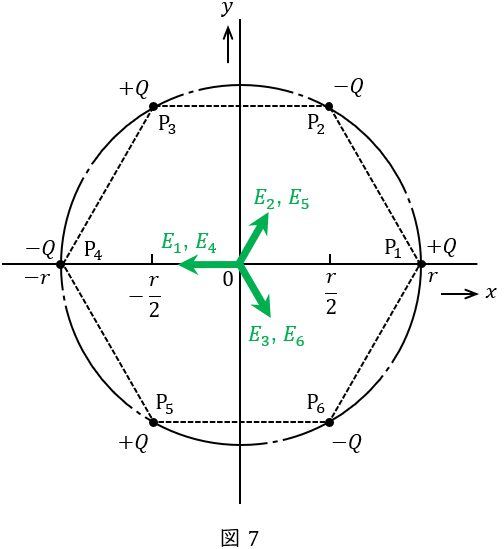
原点から各電荷までの距離は等しいため,それぞれの電荷による原点での電界の大きさは等しい。各電荷による電界を示すと図7のようになり,図7より各電界が\( \ 120^{\circ } \ \)ずつずれており打ち消し合うことがわかるので,合成電界は\( \ 0 \ \)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは