《理論》〈電気回路〉[H22:問2]交流回路の重ね合わせの理を用いた演算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，回路の電流と消費電力に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を解答群の中から選びなさい。

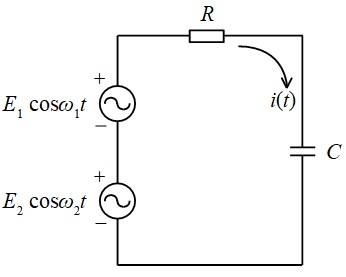
図に示す交流回路において，回路に流れる電流と消費される電力を求めたい。ただし，$ \ R = 1 \ \mathrm {[\Omega ]} \ $，$ \ C = 5 \ \mathrm {[\mu F]} \ $，$ \ E_{1} = 10 \ \mathrm {[V]} \ $，$ \ E_{2} = 16 \ \mathrm {[V]} \ $，$ \ \omega _{1} = 10^{5} \ \mathrm {[rad / s]} \ $，$ \ \omega _{2} = 2\times 10^{5} \ \mathrm {[rad / s]} \ $とする。

回路に流れる電流$ \ i \left( t \right) \ $は，重ねの理より，電圧源$ \ E_{1} \cos \omega _{1}t \ $が単独で存在するときに流れる電流$ \ I_{1} \cos \left( \omega _{1}t+\varphi _{1}\right) \ $と電圧源$ \ E_{2} \cos \omega _{2}t \ $が単独で存在するときに流れる電流$ \ I_{2} \cos \left( \omega _{2}t+\varphi _{2}\right) \ $とを足し合わせたものとなる。ここに$ \ I_{1}= \ \fbox {　（１）　} \ \mathrm {[A]} \ $，$ \ I_{2}= \ \fbox {　（２）　} \ \mathrm {[A]} \ $，$ \ \tan \varphi _{1}= \ \fbox {　（３）　} \ $となる。

次に消費電力は，周波数の異なる二つの電圧源の間の相互干渉はないから，回路を電圧源$ \ E_{1} \cos \omega _{1}t \ $のみで励振したときの消費電力$ \ \fbox {　（４）　} \ \mathrm {[W]} \ $と電圧源$ \ E_{2} \cos \omega _{2}t \ $のみで励振したときの消費電力との和で表すことができ，$ \ \fbox {　（５）　} \ \mathrm {[W]} \ $となる。

\[
\begin{eqnarray}
&（イ）&　\frac {10\sqrt {3}}{3}　　　　　&（ロ）&　\frac {8\sqrt {3}}{3}　　　　　&（ハ）&　2 \\[ 5pt ] &（ニ）&　4\sqrt {2}　　　　　&（ホ）&　15　　　　　&（ヘ）&　10 \\[ 5pt ] &（ト）&　58　　　　　&（チ）&　8\sqrt {2}　　　　　&（リ）&　20 \\[ 5pt ] &（ヌ）&　74　　　　　&（ル）&　2\sqrt {5}　　　　&（ヲ）&　86 \\[ 5pt ] &（ワ）&　5\sqrt {2}　　　　　&（カ）&　3　　　　　&（ヨ）&　4 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流回路における重ね合わせの理の適用と消費電力の導出に関する問題です。
交流も直流と同じように重ね合わせの理が適用できます。(4)以降の消費電力の導出には実効値を使用することに注意して下さい。

1.抵抗，コイル，コンデンサの電圧$ \ V \ \mathrm {[V]} \ $と電流$ \ I \ \mathrm {[A]} \ $の関係
抵抗$ \ R \ \mathrm {[\Omega ]} \ $，コイル$ \ L \ \mathrm {[H]} \ $，コンデンサ$ \ C \ \mathrm {[F]} \ $があり，電源の角周波数$ \ \omega \ \mathrm {[rad / s]} \ $及び周波数$ \ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
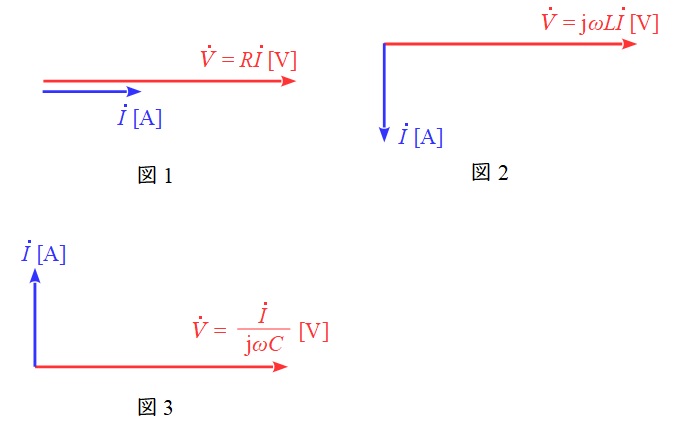
\] となります。この関係をベクトル図に表すと，図1～図3となります。

2.有効電力$ \ P \ \mathrm {[W]} \ $と無効電力$ \ Q \ \mathrm {[var]} \ $
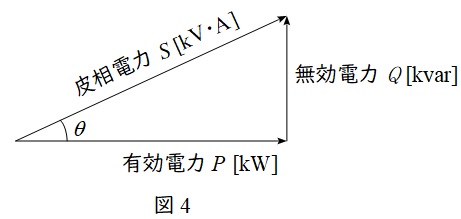
抵抗で消費される電力を有効電力$ \ P \ \mathrm {[W]} \ $，リアクタンスで消費もしくは供給される電力を無効電力$ \ Q \ \mathrm {[var]} \ $と呼び，図4のようにベクトル図を描きます。さらに，有効電力$ \ P \ \mathrm {[W]} \ $と無効電力$ \ Q \ \mathrm {[var]} \ $のベクトル和は皮相電力$ \ S \ \mathrm {[V\cdot A]} \ $と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図4において，力率は$ \ \cos \theta \ $で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

また，線路に電流$ \ I \ \mathrm {[A]} \ $が流れているとき，皮相電力$ \ S \ \mathrm {[V\cdot A]} \ $，有効電力$ \ P \ \mathrm {[W]} \ $，無効電力$ \ Q \ \mathrm {[var]} \ $は，インピーダンスを$ \ Z \ \mathrm {[\Omega ]} \ $，抵抗を$ \ R \ \mathrm {[\Omega ]} \ $，リアクタンスを$ \ X \ \mathrm {[\Omega ]} \ $とすると，
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ] P &=&RI^{2} \\[ 5pt ] Q &=&XI^{2} \\[ 5pt ] \end{eqnarray}
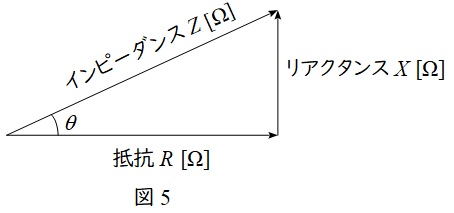
\] となるため，$ \ Z \ \mathrm {[\Omega ]} \ $，$ \ R \ \mathrm {[\Omega ]} \ $，$ \ X \ \mathrm {[\Omega ]} \ $に関しても電力と同様な図5のような関係を描くことができます。

3.重ね(重ね合わせ)の理
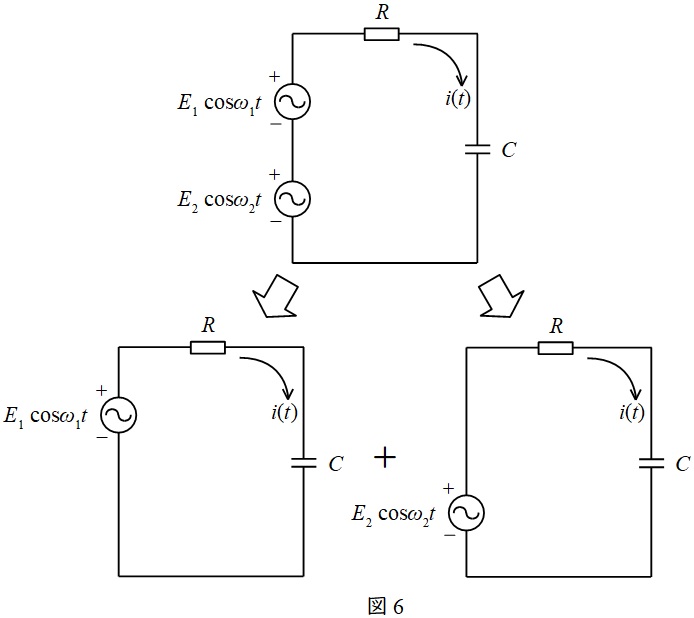
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。
したがって，本問の回路は図6のように分けて考えることができます。

【解答】

(1)解答：ル
電圧源$ \ E_{1} \cos \omega _{1}t \ $のときのみの回路のインピーダンス$ \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
{\dot Z}_{1} &=&R+\frac {1}{\mathrm {j}\omega_{1} C} \\[ 5pt ] &=&1+\frac {1}{\mathrm {j}10^{5}\times 5\times 10^{-6}} \\[ 5pt ] &=&1-\mathrm {j}2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ$ \ Z_{1} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
Z_{1} &=&\sqrt {1^{2}+2^{2}} \\[ 5pt ] &=&\sqrt {5} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，電流の振幅$ \ I_{1} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{1} &=&\frac {E_{1}}{Z_{1}} \\[ 5pt ] &=&\frac {10}{\sqrt {5}} \\[ 5pt ] &=&\frac {10}{\sqrt {5}}\times \frac {\sqrt {5}}{\sqrt {5}} \\[ 5pt ] &=&\frac {10\sqrt {5}}{5} \\[ 5pt ] &=&2\sqrt {5} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
電圧源$ \ E_{2} \cos \omega _{2}t \ $のときのみの回路のインピーダンス$ \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
{\dot Z}_{2} &=&R+\frac {1}{\mathrm {j}\omega_{2} C} \\[ 5pt ] &=&1+\frac {1}{\mathrm {j}2\times 10^{5}\times 5\times 10^{-6}} \\[ 5pt ] &=&1-\mathrm {j}1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ$ \ Z_{2} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
Z_{2} &=&\sqrt {1^{2}+1^{2}} \\[ 5pt ] &=&\sqrt {2} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，電流の振幅$ \ I_{2} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{2} &=&\frac {E_{2}}{Z_{2}} \\[ 5pt ] &=&\frac {16}{\sqrt {2}} \\[ 5pt ] &=&\frac {16}{\sqrt {2}}\times \frac {\sqrt {2}}{\sqrt {2}} \\[ 5pt ] &=&\frac {16\sqrt {2}}{2} \\[ 5pt ] &=&8\sqrt {2} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
(1)より，複素電流$ \ {\dot I}_{1} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{1} &=&\frac {{\dot E}_{1}}{{\dot Z}_{1}} \\[ 5pt ] &=&\frac {{\dot E}_{1}}{1-\mathrm {j}2} \\[ 5pt ] &=&\frac {{\dot E}_{1}}{1-\mathrm {j}2}\times \frac {1+\mathrm {j}2}{1+\mathrm {j}2} \\[ 5pt ] &=&\frac {{\dot E}_{1}}{1^{2}+2^{2}}\left( 1+\mathrm {j}2\right) \\[ 5pt ] &=&\frac {{\dot E}_{1}}{5}\left( 1+\mathrm {j}2\right) \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ \tan \varphi _{1} \ $は，
\[
\begin{eqnarray}
\tan \varphi _{1} &=&\frac {2}{1}\\[ 5pt ] &=&2 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
電圧源$ \ E_{1} \cos \omega _{1}t \ $のときのみの消費電力$ \ P_{1} \ \mathrm {[W]} \ $は，電流の実効値が$ \ \displaystyle \frac {I_{1}}{\sqrt {2}} \ $であることから，
\[
\begin{eqnarray}
P_{1} &=&R\left( \frac {I_{1}}{\sqrt {2}}\right) ^{2} \\[ 5pt ] &=&1\times \left( \frac {2\sqrt {5}}{\sqrt {2}}\right) ^{2} \\[ 5pt ] &=&1\times \frac {20}{2} \\[ 5pt ] &=&10 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
電圧源$ \ E_{2} \cos \omega _{2}t \ $のときのみの消費電力$ \ P_{2} \ \mathrm {[W]} \ $は，電流の実効値が$ \ \displaystyle \frac {I_{2}}{\sqrt {2}} \ $であることから，
\[
\begin{eqnarray}
P_{2} &=&R\left( \frac {I_{2}}{\sqrt {2}}\right) ^{2} \\[ 5pt ] &=&1\times \left( \frac {8\sqrt {2}}{\sqrt {2}}\right) ^{2} \\[ 5pt ] &=&64 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となるので，消費電力の和$ \ P \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P &=&P_{1}+P_{2} \\[ 5pt ] &=&10+64 \\[ 5pt ] &=&74 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。